In het artikel werd de aanname gemaakt dat de trekkingen van de blokjes (en de letters) onafhaneklijk van elkaar zijn. Dat maakt de berekeningen een stuk eenvoudiger. De eerste oplossing hier maakt gebruik van die benadering. Daarna volgt de exacte oplossing.

Benadering

Kies $n$ blokjes. De kans dat daarin minstens 1 blokje rood is, is gelijk aan $1$ minus de kans dat er geen enkel blokje rood is (de complementregel), dus:

$P($minstens 1 blokje rood$) = 1 - P($geen enkel blokje rood$)$.

$$=1-\left(\frac34\right)^n.$$

Maar dit moet ook voor de andere drie kleuren blauw, geel en groen gelden, dus $P($minstens één blokje van elke kleur$)$

$$=\left(1-\left(\frac34\right)^n\right)^4.$$

Hierbij hebben de aanname gebruikt dat de trekkingen onderling onafhankelijk zijn. Deze kans moet minstens $0{,}95$ zijn. We berekenen de waarde van $n$ bij exacte gelijkheid aan $0{,}95$, dus

$$\left(1-\left(\frac34\right)^n\right)^4=0{,}95.$$

Hieruit volgt

$$1 - \left(\frac34\right)^n= 0{,}95^{\frac14}$$

en daarna

$$\left(\frac34\right)^n=1-0{,}95^{\frac14}.$$

Deze exponentiële vergelijking kan worden opgelost door

$$n=\frac{\log\left(1-0{,}95^{\frac14}\right)}{\log(\frac34)}\approx 15{,}2.$$

Het minimaal aantal te pakken blokjes is dus 16.

Exacte oplossing

We bewijzen dat de kans dat elk van de vier kleuren, gelijk verdeeld in een ‘oneindige voorraad’ blokjes, minstens één keer voorkomt in een trekking van $n$ blokjes, gelijk is aan

$$1-4\cdot\left(\frac34\right)^n+6\cdot\left(\frac12\right)^n-4\cdot\left(\frac14\right)^n.$$

Dat doen we door eerst voor twee gebeurtenissen $A$ en $B$ de volgende kansregel te bewijzen:

$$P(\bar{A}\cap\bar{B}) = 1 - P(A)-P(B)+P(A\cap B).$$

$(1)$

Hierin is $\bar{A}$ het complement van $A$ (het tegengestelde van die gebeurtenis $A$) en $A \cap B$ is de doorsnede van de twee gebeurtenissen $A$ en $B$ (de gemeenschappelijke elementen).

Bewijs.  De complementregel (ontkenningsregel) uit de kansrekening is:

$$P(\bar{A}) = 1-P(A)$$

en de algemene somregel (optelregel) is:

$$P(A\cup B) = P(A)+P(B)-P(A\cap B).$$

$(2)$

Hierin is $A\cup B$ de vereniging van twee gebeurtenissen $A$ en $B$ (gebeurtenissen die in of $A$, in $B$ of in beide zitten). Verwissel de termen met vereniging en doorsnede uit $(2)$:

$$P(A\cap B)=P(A)+P(B)-P(A\cup B).$$

$(2a)$

Pas de ontkenningsregel toe op de laatste term uit vergelijking $(2a)$:

$$P(A\cap B)=P(A)+P(B)-\left(1-P(\overline{A\cup B})\right).$$

Maar $\overline{A\cup B}$, het complement van $A \cup B$, is gelijk aan $\bar{A} \cap \bar{B}$, bijvoorbeeld te zien met behulp van onderstaand plaatje:

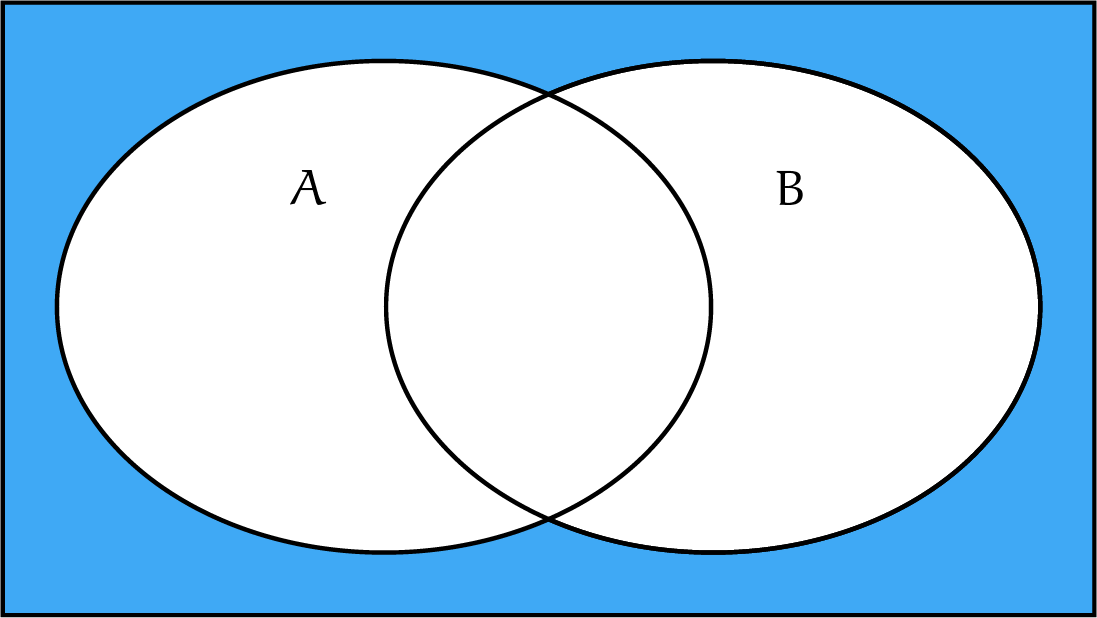
$\overline{A\cup B}=\bar{A}\cap\bar{B}$.

We krijgen dus:   

$$P(A\cap B)=P(A)+P(B)-\left(1-P(\bar A \cap \bar B)\right).$$

Haakjes uitwerken levert:

$$P(A\cap B)=P(A)+P(B)-a+P(\bar A\cap\bar B).$$

Breng de eerste drie termen aan de rechterkant naar links. Van rechts naar links lezend krijgen we de te bewijzen regel:

$$P(\bar{A}\cap\bar{B}) = 1 - P(A)-P(B)+P(A\cap B).$$

$(1)$

Intuïtief is deze regel ook wel logisch: de kans op het gebied ‘buiten’ $A\cup B$ (ofwel $\bar A\cap\bar B$; zie de figuur) is gelijk aan $1$ minus de ‘kans op $A$’ en minus de ‘kans op $B$’, maar dan hebben we de kans op de doorsnede van $A$ en $B$ wel dubbel van die 1 afgehaald, dus is een correctieterm $+P(A\cap B)$ nodig.

Er is een generalisatie mogelijk van vergelijking $(1)$, die we hier niet expliciet bewijzen. Voor drie gebeurtenissen geldt:

$$P(\bar A\cap\bar B\cap\bar C)=1-P(A)-P(B)-P(C)+P(A\cap B)+P(A\cap C)+P(B\cap C)-P(A\cap B\cap C).$$

Merk op dat 5^e, 6^e en 7^e term aan de rechterkant van deze gelijkheid precies de drie combinaties van twee uit drie gebeurtenissen bevatten ($AB$, $AC$ en $BC$).

Nog verder generaliserend komen we tot:

$$P\left(\bigcap^n_{i=1}{\bar A}_i\right)=1-\sum_{i=1}^nP(A_i)+\sum_{i\neq j}P(A_i\cap A_j) -\sum_{i\neq j\neq k}P(A_i\cap A_j\cap A_k) + \cdots +(-1)^nP\left(\bigcap_{i=1}^n A_j\right).$$

De benodigde regel die we uit deze serie van gelijkheden moeten hebben voor onze vraag over de blokjes in 4 kleuren is uiteraard het geval voor $n = 4$:

$$$$

$$P(\bar A\cap\bar B\cap\bar C\cap\bar D) = 1-P(A)-P(B)-P(C)-P(D)\\+P(A\cap B)+P(A\cap C)+P(A\cap D)+P(B\cap C)+P(B\cap D)+P(C\cap D)\\-P(A\cap B\cap C)-P(A\cap B\cap D)-P(A\cap C\cap D)-P(B\cap C\cap D)\\+P(A\cap B\cap C\cap D).$$

$(3)$

Merk weer op dat de tweede regel van de gelijkheid de zes combinaties van 2 uit 4 mogelijkheden bevat en regel drie de vier combinaties van 3 uit 4 mogelijke gebeurtenissen bevat.

Nu keren we terug naar het startprobleem van ‘Alle zesentwintig’ uit het artikel. De vraag was daar:

Hoeveel blokjes moet je (willekeurig gekozen, dus zonder naar de kleur te kijken) pakken om, met een zekerheid van minstens 95%, elk van de vier kleuren minimaal één keer vertegenwoordigd te hebben?

Om die vraag te beantwoorden moeten we eerst de kans bepalen dat elk van de vier kleuren minstens één keer vertegenwoordigd is, afhankelijk van het aantal trekkingen.

Stel nu:

• $A$ is de gebeurtenis: ‘geen enkele keer kleur $a$ bij trekking van $n$ blokjes’;
• $B$ is de gebeurtenis: ‘geen enkele keer kleur $b$ bij trekking van $n$ blokjes’,

et cetera.

Maar dan geldt:

• $\bar A$ is de gebeurtenis: ‘minstens één keer de kleur $a$ bij trekking van $n$ blokjes’;
• $\bar B$ is de gebeurtenis: ‘minstens één keer de kleur $b$ bij trekking van $n$ blokjes’,

etc.

Dan geldt bijvoorbeeld: $P(A)=\left(\frac34\right)^n$, omdat in elke trekking (wegens de oneindigheid van de populatie) de kans dat een aselect getrokken blokje niet kleur $a$ heeft, $\frac34$ is.

Evenzo is $P(B)=\left(\frac34\right)^n$, et cetera.

Verder geldt $P(A\cap B) = \left(\frac24\right)^n = \left(\frac12\right)^n$ (kans op niet kleur $a$ of $b$ is bij elke trekking $\frac12$), enzovoort.

Net zo wordt $P(A\cap B\cap C) = \left(\frac14\right)^n$ en daarmee ook de andere drie termen.

NB: $P(A\cap B\cap C\cap D)=0$ want dat is de kans dat geen van de vier kleuren in een trekking van $n$ blokjes voorkomt. Dat kan niet, want er zijn alleen maar die vier kleuren.

De kans is dus te berekenen met formule $(3)$:

$$1-4\cdot\left(\frac34\right)^n+6\cdot\left(\frac12\right)^n-4\cdot\left(\frac14\right)^n.$$

Grappig in deze formule is om te zie dat voor $n=1$, $n=2$ en $n=3$ de kans $0$ is. Dat klopt, want bij minder dan 4 trekkingen kun je ook nog niet alle vier kleuren gehad hebben!

Voor $n=4$ volgt de kans $\frac{3}{32} = 0{,}09375$, die enige uit de serie ook eenvoudig berekend kan worden, door $\frac34\cdot\frac12\cdot\frac14$, niet geheel toevallig het product van de drie grondtallen in de exponentiële uitdrukking $(3)$.

In het artikel gebruikten we de ‘benaderingskans’

$$\left(1=\left(\frac34\right)^n\right)^4.$$

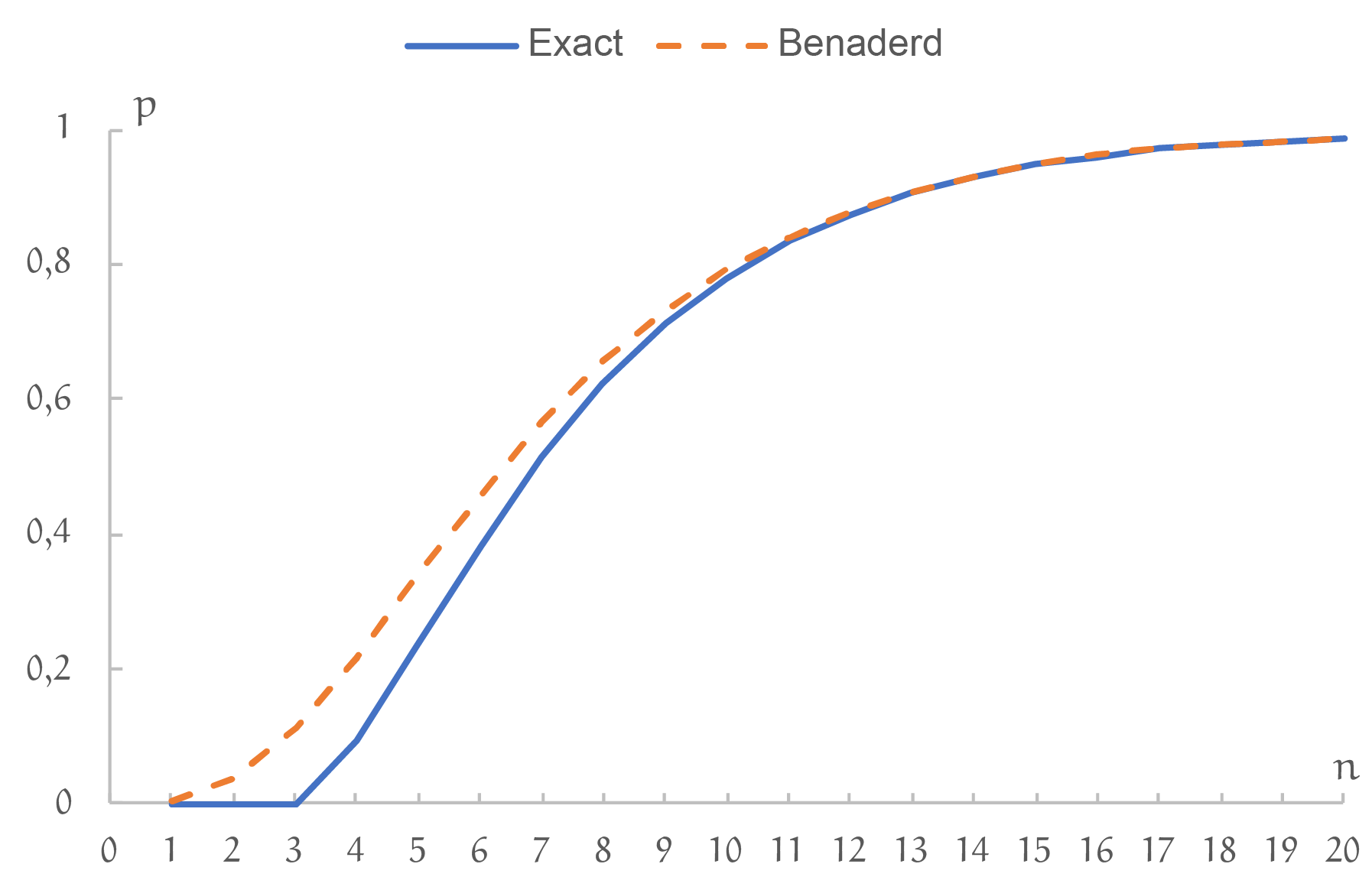
In de tabel en grafiek hieronder geven we de eerste 20 waarden van beide formules. Te zien is dat bij beide methoden voor n = 16 de kans voor het eerst boven de 95% uit komt.

Merk op dat de ‘exacte’ kans ook niet helemaal juist is, omdat we in de praktijk natuurlijk nooit een oneindige voorraad blokjes kunnen hebben. Omdat we echter gesteld hebben dat "een zeer grote hoeveelheid blokjes" is, mogen we aannemen dat de kansen verwaarloosbaar gaan verschillen. We mogen zeggen dat de kleurenkansen met aan zekerheid grenzende waarschijnlijkheid telkens gelijk aan $\frac34$, $\frac12$ en $\frac14$ zijn...

$n$	$p$			$n$	$p$
	exact	benaderd			exact	benaderd
$1$	$0$	$0{,}0039$		$11$	$0{,}834$	$0{,}8415$
$2$	$0$	$0{,}0366$		$12$	$0{,}8748$	$0{,}8792$
$3$	$0$	$0{,}1117$		$13$	$0{,}9057$	$0{,}9083$
$4$	$0{,}0938$	$0{,}2184$		$14$	$0{,}9291$	$0{,}9306$
$5$	$0{,}2344$	$0{,}3384$		$15$	$0{,}9467$	$0{,}9476$
$6$	$0{,}3809$	$0{,}4566$		$16$	$0{,}9600$	$0{,}9605$
$7$	$0{,}5127$	$0{,}5638$		$17$	$0{,}9700$	$0{,}9703$
$8$	$0{,}6229$	$0{,}6558$		$18$	$0{,}9775$	$0{,}9776$
$9$	$0{,}7114$	$0{,}7318$		$19$	$0{,}9831$	$0{,}9832$
$10$	$0{,}7806$	$0{,}7931$		$20$	$0{,}9873$	$0{,}9874$