Driehoeken en vierkanten

Het blauwe driehokje is 1/32^ste deel van het grote vierkant.

Hoe lang is de tunnel?

Noem de lengte van de tunnel $L$ en de lengte van de trein $l.$ Noem de snelheid van de trein ten opzichte van een stilstaande seinwachter naast het spoor $V$ en jouw loopsnelheid ten opzichte van de trein $v.$

Je snelheid ten opzichte van de seinwachter is dus $V - v.$ De tijd dat het donker is voor jou is dus $\frac{L}{V - v}.$ In die tijd heeft de trein een afstand $L + l$ afgelegd. Die tijd is $\frac{L + l}{V}.$ Gelijkstellen van deze twee tijden geeft na een beetje rekenen: $\frac{V}{v}=\frac{L}{l} + 1.$ Nu is $\frac{V}{v} = 50.$ Dus $\frac{L}{l} = 49.$ Er passen dus $49$ van deze treinen in de tunnel.

Gelukkig 2019

De volgende getallen kunnen gemaakt worden, bijvoorbeeld:

0 = 0 × 1 × 2 × 9
1 = 2 – 1 + 0 × 9
2 = 2 + 0 × 1 × 9
3 = 1 + 2 + 0 × 9
4 = √9 + 1 + 0 × 2
5 = √9 + 2 + 0 × 1
6 = √9 + 1 + 2 + 0
7 = √9 × 2 + 1 + 0
8 = 9 – 1 + 0 × 2
9 = 9 + 0 × 1 × 2
10 = 9 + 1 + 0 × 2
11 = 9 + 2 + 0 × 1
12 = 9 + 1 + 2 + 0
13 = √9! × 2 + 1 + 0
14 = 9 + 10 / 2
15 = 10 + 2 + √9
16 = (√9 + 1)² + 0
17 = 10 + 9 – 2
18 = 2 × 9 + 0 × 1
19 = 2 × 9 + 1 + 0
20 = 19 + 2⁰
21 = 19 + 2 + 0
22 = 20 + √9 – 1
23 = 20 + 1 × √9
24 = 20 + 1 + √9
25 = 20 + √9! – 1
26 = 20 + 1 × √9!
27 = 20 + √9! + 1
28 = 20 + 9 – 1
29 = 20 + 1 × 9
30 = 20 + 9 + 1
31 = ??

Het kleinste getal waarbij het niet meer lukt is dus $31.$

Drie keer knippen

1. Neem een rechthoek van $15 \times 24.$ De rechthoeken hebben de maten: $6 \times 6 = 1 \times 36,$ $8 \times 9 = 72 = 2 \times 36,$ $6 \times 18 = 108 = 3 \times 36,$ $9 \times 16 = 144 = 4 \times 36.$
2. Neem een rechthoek van $4 \times 6.$ De rechthoeken hebben dan de maten: $1 \times 1,$ $1 \times 3,$ $1 \times 5,$ $3 \times 5.$ De bijbehorende oppervlaktes zijn: $4, 8, 12, 16.$

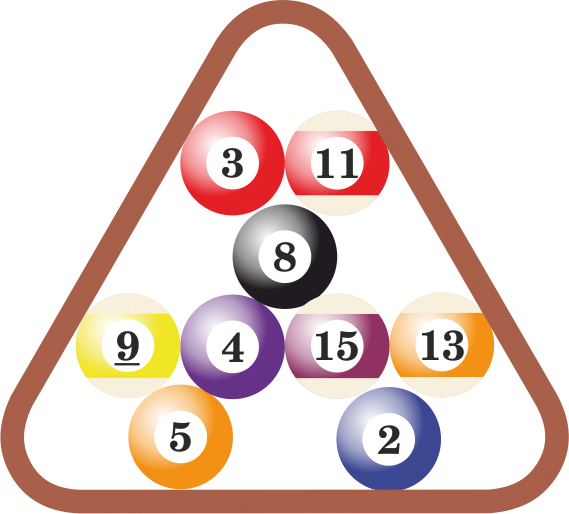
Poolrack

6 ballen: