Oplossing 330 [niveau oOO]

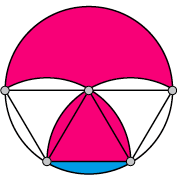Links zie je een logo dat een mediabedrijf groot op een muur wil laten verven. De straal van elke cirkel is 1 meter. Hoeveel vierkante meter roze verf is er nodig?
Oplossing. Zie figuur rechts. Het roze deel bestaat uit 3 halve cirkels (met straal 1 meter) minus 3 maal 2 maal het blauwe deel plus de gelijkzijdige driehoek (met zijde 1 meter) plus 3 maal het
blauwe deel. Het blauwe deel vormt samen met de gelijkzijdige driehoek precies ${1 \over 6}$ deel van de cirkel. De oppervlakte van de gelijkzijdige driehoek is ${1 \over 4}\sqrt3$, de oppervlakte van de cirkel is $\pi$. Dus de oppervlakte van het roze deel is $3({1 \over 2} \pi – 2({1 \over 6}\pi – {1 \over 4} \sqrt3)) + {1 \over 4} \sqrt3 + 3( {1 \over 6} \pi – {1 \over 4} \sqrt3) = \pi + \sqrt3$ m².

 

Oplossing 331 [niveau oOO]

Leg een aantal munten op een rij, allemaal met ‘kop’ naar boven. Draai van links naar rechts eerst 1, dan 2, dan 3, enzovoort, munten om (dit zijn de zetten). Je begint steeds met de volgende munt na de laatst omgedraaide om een volgende zet te doen. Als je aan het eind van de muntenrij bent aangekomen, ga je gewoon verder aan het begin van de rij.

1. In hoeveel zetten liggen alle munten weer met ‘kop’ boven, als je start met 1, 3, 4 of 5 munten?
2. Bereik je met elk aantal munten op een gegeven moment weer de situatie dat alle munten met ‘kop’ boven liggen?

Oplossing. Er geldt: $1 + 2 + ... + n = {1 \over 2} n(n + 1)$ (dit zijn de zogeheten driehoeksgetallen). Na $n$ zetten zijn er ${1 \over 2} n(n + 1)$ munten omgedraaid. Elke munt moet een even aantal malen worden omgedraaid. Stel we gaan uit van $m$ munten, dan moet gelden dat ${1 \over 2} n(n + 1)$ een veelvoud is van $2m$.

1. De rij driehoeksgetallen is $1, 3, 6, 10, 15, 21, 28, 36, ...$. Voor $1$ munt is $n = 3$, want ${1 \over 2} · 3 · 4 = 6$ is een veelvoud van $2$. Voor $3$ munten is $n = 3$, want ${1 \over 2} · 3 · 4 = 6$ is een veelvoud van $6$. Voor $4$ munten is $n = 15$, want ${1 \over 2} · 15 · 16 = 120$ is een veelvoud van $8$. Voor $5$ munten is $n = 4$, want ${1 \over 2} · 4 · 5 = 10$ is een veelvoud van $10$.
2. Je kunt voor elk aantal munten weer terugkomen in de oorspronkelijke situatie. Als $m$ even is, dan voldoet $n = 4m – 1$, want ${1 \over 2} · (4m – 1) · 4m = 2m(4m – 1)$. Als $m$ een viervoud $+ 1$ is (zeg $m = 4k + 1$), dan voldoet $n = m – 1$, want ${1 \over 2} · 4k · m = 2mk$. Als $m$ een viervoud $– 1$ is (zeg $m = 4k – 1$), dan voldoet $n = m$, want ${1 \over 2} · m · 4k = 2mk$.

 

Oplossing 332 [niveau ooO]

Gegeven zijn drie gehele getallen $a, b$ en $c$ met de volgende eigenschap: het verschil van twee van deze getallen is deelbaar door het derde. Bijvoorbeeld de getallen $2, –3$ en $5$ voldoen hieraan: het verschil van $2$ en $–3$ is $5$ (en dat is deelbaar door $5$), het verschil van $2$ en $5$ is $3$ (en dat is deelbaar door $–3$) en het verschil van $–3$ en $5$ is $8$ (en dat is deelbaar door $2$).

1. Bewijs dat $a, b$ en $c$ niet allemaal positief kunnen zijn.

2. Veronderstel nu verder dat a, b en c ook geen gemeenschappelijke factoren hebben (behalve natuurlijk $1$ en $–1$). Is het waar dat één van de drie getallen gelijk moet zijn aan $1$, of $2$, of $–1$, of $–2$?

Oplossing. We mogen veronderstellen dat a ≤ b ≤ c.

1. Als $0 < a ≤ b ≤ c$, dan geldt (aangezien een deler $c$ kleiner dan of gelijk is aan $b – a$) dat $0 < c ≤ b – a < b ≤ c$. Maar hier staat $c < c$: een tegenspraak.
2. Er moet gelden dat $a < 0 < b ≤ c$ of $a ≤ b < 0 < c$. Het laatste geval is te herleiden tot het eerste geval door $a, b$ en $c$ te vermenigvuldigen met $–1$. We hoeven dus alleen het eerste geval te bekijken. Vervang $a$ door $–d$, dan is $d > 0$. De deelbaarheidskenmerken vertalen zich tot $(a)\; c – b = ud$, $(b)\; c + d = vb$ en $(c)\; b + d = wc$, voor gehele getallen $u, v$ en $w$. Substitueer $b = c – ud$ in de twee andere vergelijkingen. We vinden $(b’)\; c + d = vc – uvd$ en $(c’)\; c + d – ud = wc$. De laatste vergelijking $(c’)$ is te herschrijven tot $(w – 1)c + (u – 1)d = 0$. Als $u = 0$ (dus $b = c$), dan volgt $(w – 1)c = d$. Dat betekent dat $c$ een deler is van $d$. Dit betekent (aangezien $a, b$ en $c$ geen gemeenschappelijke delers hebben) dat $c = 1$. Als $u = 1$, dan volgt ook dat $w = 1$. De drie deelbaarheidskenmerken zijn nu te schrijven als $(a)\; c – b = d$, $(b)\; c + d = vb$ en $(c)\; b + d = c$. We substitueren nu $(c)$ in $(b)$ en vinden $b + 2d = vb$. $b$ is een deler van $2a$, maar $a$ en $b$ hebben geen gemeenschappelijke delers, dus is $b$ een deler van $2$.

 

Oplossing 333 [niveau ooO]

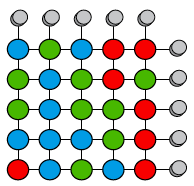
In een 5 × 5-bord staat in ieder hokje een lampje. De lampjes hebben de kleuren groen, blauw en rood. Aan iedere rij en kolom is een knopje verbonden. Bij het indrukken vanhet knopje dat bij een rij hoort, worden alle groene lampjes in die rij blauw, alle blauwe lampjes worden rood en alle rode lampjes groen. Is het vanuit iedere startpositie mogelijk om een kleur volledig van het bord te elimineren?
Oplossing. De gewenste eindsituaties zijn situaties waarbij een kleur volledig is geëlimineerd. We mogen veronderstellen dat dat de kleur rood is. We noemen een dergelijke situatie een niet-rood-situatie. Immers, als blauw volledig is geëlimineerd, dan kunnen we door alle rij-knopjes te bedienen alle lampjes opschuiven. De ontbrekende kleur blauw wordt de ontbrekende kleur rood. En als groen ontbreekt, dan kan door tweemaal alle rij-knopjes te bedienen eveneens rood de ontbrekende kleur worden. Het aantal mogelijke eindsituaties is 2²⁵. We laten nu zien dat er meer beginsituaties zijn dan beginsituaties die kunnen worden overgevoerd naar een niet-rood-situatie. Zodoende is er een startpositie te vinden waarbij nooit een kleur te elimineren is. Hoeveel beginsituaties kunnen op een niet-roodsituatie overgaan? We draaien de vraag om. In hoeveel beginsituaties kun je vanuit een niet-rood-situatie hooguit terecht komen? Je kunt op ieder van de 10 knoppen 0, 1 of 2 maal drukken, dus dat zijn hooguit 3¹⁰ mogelijkheden. Maar met 9 knoppen kun je de 10de knop bedienen. Stel dat je de eerste rijknop wilt bedienen, dan kun je daarvoor in de plaats alle kolomknoppen indrukken en tevens de overige rijknoppen 2 maal bedienen. Dus vanuit 2²⁵ niet-rood-situaties kun je 2²⁵ · 3⁹ beginsituaties bereiken en dat is minder dan 3²⁵, het totaal aantal beginsituaties.