BrandpuNt en brAndkRoMmEn

Zo rond 200 jaar voor Christus schreef de Griekse wiskundige Diocles een boek met als titel Over brandende spiegels $(\Pi\epsilon\rho\grave{\iota}\ \pi\upsilon\rho\acute{\iota}\omega\nu)$. Daarin vind je de bekende eigenschap van een parabool die weergegeven wordt in figuur 1.

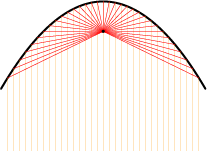
Lichtstralen die invallen op een parabolische spiegel en die evenwijdig zijn met de as van die parabool worden weerkaatst door het brandpunt van de parabool. Diocles is nu nog vooral bekend door zijn cissoïde, een kromme die hij als eerste bestudeerde en gebruikte om een van de Delische problemen uit de oudheid op te lossen: de verdubbeling van de kubus.
Archimedes gebruikte bovenstaande eigenschap van de parabool in 212 voor Christus om bij de belegering van Syracuse de vloot van Marcus Claudius Marcellus in brand te steken, zo vertelt de overlevering.

Pas veel later werd er ook gekeken naar wat er precies gebeurt indien lichtstralen invallen op een gekromd oppervlak dat niet parabolisch maar bijvoorbeeld cilindervormig is. Het resultaat zie je soms als je op een zonnig terras koffie zit te drinken, op het oppervlak van de koffie, zoals in figuur 2. In figuur 3, waar de zon wordt weerkaatst in een cilinder, is het effect duidelijker.

 

Wat we hier zien, wordt een brandkromme of kaustiek genoemd. Graaf Ehrenfried Walter von Tschirnhaus (1651-1708) was de eerste die dergelijke krommen die ontstaan bij weerkaatsing van het licht, onderzocht, rond 1680. Hij gebruikte het Latijnse woord Caustica, dat afgeleid is van het Griekse
$\kappa \alpha \upsilon \sigma \tau \iota \kappa o \varsigma$ 'die kan doen branden', van het werkwoord $\kappa \alpha \iota \varepsilon \iota \nu$: branden.
De grote wiskundige Johann Bernoulli (1667-1748) zei het zo

Als de zonnestralen op een hol deel van  een curve vallen, dan zullen ze door hun weerspiegeling een andere curve vormen, die van de heer Tschirnhaus de naam 'Kaustische curve' gekregen heeft en waarvan hij de eerste ontdekker is geweest.

Toevallig is de koffiekopkaustiek (figuur 2 en 3) ook de eerste brandkromme die Tschirnhaus bestudeerde. (Merk op dat er in 1680 al koffie was in Europa.)

DE KoFfIEkOPkAUSTieK

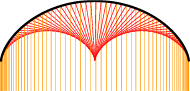
We proberen de situatie grafisch voor te stellen. We vertrekken van een cirkel, en veronderstellen dat de lichtstralen in het vlak van de cirkel liggen. Als we voldoende lichtstralen tekenen en hun weerkaatsingen, dan krijgen we een goed beeld van de brandkromme (zie figuur 4).

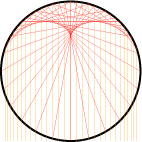
Je kan de kromme die zo ontstaat zelf maken. Teken op een stuk hout een cirkel, en klop dan op de cirkel en op gelijke afstand van elkaar een even aantal nageltjes in het hout. Nummer de nageltjes zoals in  figuur 5. Als je dan met garen het nageltje op positie $i$ verbindt met dat op positie $3i$, dan krijg je wat je ziet in figuur 5.

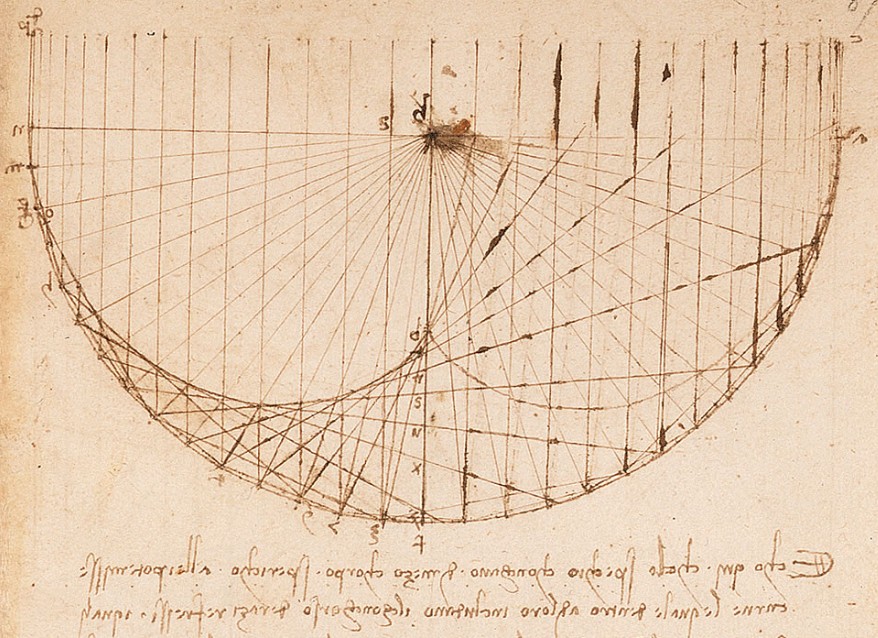
Het is leuk op te merken dat we bij Leonardo Da Vinci - de wetenschapper/uitvinder die erom bekend staat dat hij zijn tijd ver vooruit was - de tekening in figuur 6 vinden, in zijn boek Codex Arundel dat dateert van rond 1500. (Toen was er nog geen koffie in Europa!)

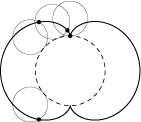
De kromme in kwestie is (de helft van) een nierkromme of nefroïde. Het is een kromme die behoort tot de klasse krommen die we epicycloïden noemen en die ontstaan door een cirkel om een andere cirkel te rollen. We volgen hierbij de beweging van een punt van de rollende cirkel (zie figuur 7).

BRAnDKROMmEN IN DETAiL.

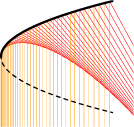
We bekijken nu de koffiekopkaustiek wat meer in detail en gaan na hoe deze precies ontstaat. In figuur 8 nemen we een close-up van een stukje. Let op de verticale rechte. Op deze rechte ligt een punt van de kaustiek, het is aangeduid in de rechterfiguur. Behalve dit punt zijn ook een aantal van de weerkaatste stralen getekend die in de buurt van dit punt komen. Als we het snijpunt van deze stralen met de verticale rechte volgen, beginnend met de stralen door 1 en 2, dan zie je dat de hoogte van dit snijpunt afneemt tot het een minimum bereikt, en dan weer toeneemt. Op het ogenblik dat het minimum bereikt wordt, zitten we op de kaustiek. We kunnen dus de $y$-waarde van dit punt van de kaustiek in principe berekenen met behulp van afgeleiden.

Dit is ook in het algemeen zo bij brandkrommen.
We moeten ook weten hoe lichtstralen weerkaatst worden. Dit gebeurt zoals aangegeven in figuur 9.

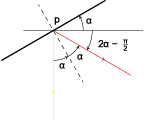
In deze figuur zie je een spiegel die door het punt $p$ gaat (dikke lijn), een lichtstraal (verticale lijn) die invalt in $p$ en weerkaatst wordt door de spiegel, volgens de wet van de weerkaatsing. Als de spiegel een hoek $\alpha$ maakt met een horizontale rechte, dan is de hoek die de weerkaatste straal maakt met die horizontale rechte gelijk aan $2\alpha-\frac{\pi}{2}$, zoals je kan zien op de figuur. Indien de spiegel gekromd is in $p$, dan bekijk je de raaklijn aan de kromme in $p$ als spiegel om de weerkaatste straal te bepalen. Herinner je dat de richtingscoëfficiënt van die raaklijn gelijk is aan $\mbox{tg } \alpha$: we kunnen dus voor een gegeven kromme berekenen wat die hoek $\alpha$ is.

OPDRACHT 1 Indien de raaklijn in het punt $p$ richtingscoëfficiënt $m$ heeft, wat is dan de richtingscoëfficiënt van de weerkaatste straal? Oplossing: $\frac{m^2-1}{2m}$.

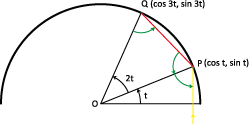
Specifiek in het geval van de koffiekopkaustiek kunnen we nu verklaren waarom we in figuur 5 als resultaat deze kromme krijgen. In figuur 10 zie je een straal die invalt op de cirkel in een punt $P$, waarbij de rechte $OP$ een hoek $t$ maakt met de horizontale as. Merk op dat de drie groene hoeken op de figuur gelijk zijn aan $\frac{\pi}{2}-t$. Dit is een gevolg van de wet van de weerkaatsing en van het feit dat $\triangle OPQ$ gelijkbenig is, waarbij $Q$ het punt van de cirkel is waar de weerkaatste straal doorgaat. De hoek tussen de horizontale as en de rechte $OQ$ is hierdoor gelijk aan $3t$. De weerkaatste straal loopt dus tussen het punt met hoek $t$ en het punt met hoek $3t$.
Met deze figuur als basis kunnen we ook de vergelijkingen van de koffiekopkaustiek vinden (zie kadertekst).

VERGELIJKINGEN VOOR DE KOFFIEKOPKAUSTIEK.

Stel dat de verticale rechte in figuur 8 vergelijking $x=a$ heeft. Om het punt van de brandkromme te vinden dat op die rechte ligt, gaan we eerst op zoek naar alle weerkaatste stralen die deze rechte snijden. In figuur 10 zie je dat zo'n weerkaatste straal voor een gegeven hoek $t$ door de punten $(\cos t, \sin t)$ en $(\cos 3t, \sin 3t)$ gaat. De rechte bepaald door deze twee punten heeft als richtingscoëfficiënt:
\[
m = \frac{\sin 3t - \sin t}{\cos 3t - \cos t} .
\]
We kunnen dit eenvoudiger schrijven door gebruik te maken van de volgende formules van Simpson:
\[
\sin a - \sin b = 2 \cos \frac{a+b}{2} \sin \frac{a-b}{2} \ , \ \ \ \cos a - \cos b = -2 \sin \frac{a+b}{2} \sin \frac{a-b}{2} .
\]
We vinden hiermee:
\[
m = \frac{\sin 3t - \sin t}{\cos 3t - \cos t} = \frac{2 \cos 2t \sin t}{-2 \sin 2t \sin t} = - \mbox{cotg } 2t .
\]
Een weerkaatste straal die door het punt $(\cos t, \sin t)$ gaat, heeft dus als richtingscoëfficiënt $-\mbox{cotg } 2t$ en de vergelijking ervan is:
\[
y-\sin t = - \mbox{cotg } 2t \cdot (x-\cos t)  .
\]
De rechte $x=a$ snijdt zo'n weerkaatste straal dus in een punt met $y$-coördinaat (of hoogte):
\[
(*) \ \ \ y = \sin t - \mbox{cotg } 2t \cdot (a-\cos t) .
\]
We zoeken de kleinste waarde die deze $y$ aanneemt als we $t$ laten variëren. Die vinden we door te eisen dat de afgeleide van $y$ naar $t$ gelijk is aan nul. Dus er moet gelden:
\[
y'=0 \ \ \ \Leftrightarrow \ \ \ \cos t + \frac{2}{\sin^2 2t} (a-\cos t) - \mbox{cotg } 2t \, \sin t = 0 .
\]
We werken deze vergelijking uit naar $a$. Dit geeft, na wat goniometrisch rekenwerk (ga dit zelf na): $a = \frac{1}{4} \cos 3t + \frac{3}{4}\cos t$ (of iets equivalent). De bijhorende $y$-waarde vinden we door deze uitdrukking voor $a$ in te vullen in $(*)$, en weer wat te herschrijven met goniometrische formules: $y = \frac{1}{4} \sin 3t + \frac{3}{4}\sin t$ (of equivalent). We kunnen dit als volgt interpreteren: voor deze waarde van $a$ heeft het punt van de brandkromme deze $y$-waarde. Of nog: het punt met coördinaten
\[
\left(\frac{1}{4} \cos 3t + \frac{3}{4}\cos t, \frac{1}{4} \sin 3t + \frac{3}{4}\sin t\right)
\]
is een punt van de brandkromme.

OPDRACHT 2. Reken het even na en maak m.b.v. het programma desmos (www.desmos.com) of met Wolframalpha (www.wolframalpha.com) een grafiek van het resultaat, ook als je niet precies dezelfde uitkomst krijgt als hierboven!

ANDERE INTERESSANTE BRANDKROMMEN.

Nadat Tschirnhaus als eerste dit soort krommen bestudeerde, stortten heel wat gerenommeerde wiskundigen zich op de studie van brandkrommen. We eindigen met enkele ontdekkingen in dit verband:
(1) De brandkromme van een parabool waarbij de lichtstralen loodrecht invallen op de as ervan (zie figuur 11) is (de helft van) een kromme die de kubische kromme van Tschirnhaus genoemd wordt.

(2) De brandkromme van een cycloïde waarbij de lichtstralen invallen zoals in figuur 12 is ... opnieuw een cycloïde die half zo groot is.

(3) De brandkromme van de functie met voorschrift $y=e^x$ waarbij de lichtstralen invallen zoals in figuur 13 is ... een kettinglijn.

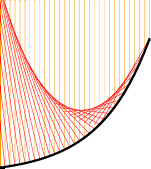
OPDRACHT 3. Reken deze laatste zelf na. Maar vertrek van $y=-e^x$ zodat de stralen van onder komen. Gebruik het resultaat van opdracht 1, bepaal in een punt met $x=t$ de vergelijking van de weerkaatste straal, en ga dan verder zoals in de uitwerking voor de koffiekopkaustiek.