De volgende puzzel gaat over lichtstralen en spiegels. We hebben het hier over ideale lichtstralen en ideale spiegels. Een ideale lichtstraal is een lichtstraal die niet uitdooft, oneindig dun is en zich kaarsrecht voortbeweegt, totdat hij ergens wordt weerkaatst. Een ideale spiegel is overal vlak en weerkaatst het licht voor 100%, en hoek van uitval van een lichtstraal is precies gelijk aan de hoek van inval. En een ideale zaklantaarn produceert een ideale lichtstraal. 

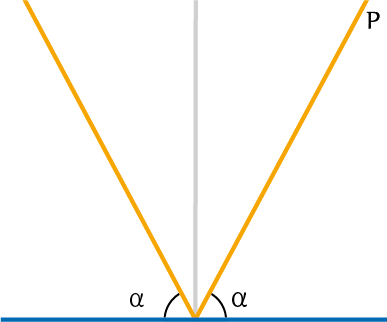
Kijk om te beginnen naar figuur 1. Iemand op de plaats $P$ schijnt met een ideale zaklantaarn op een ideale spiegel. Alleen als de lichtstraal loodrecht op de spiegel terecht komt, dan komt de weerkaatste lichtstraal parallel weer terug. Bij andere invalshoeken is de teruggekaatste lichtstraal niet parallel aan de invallende lichtstraal.

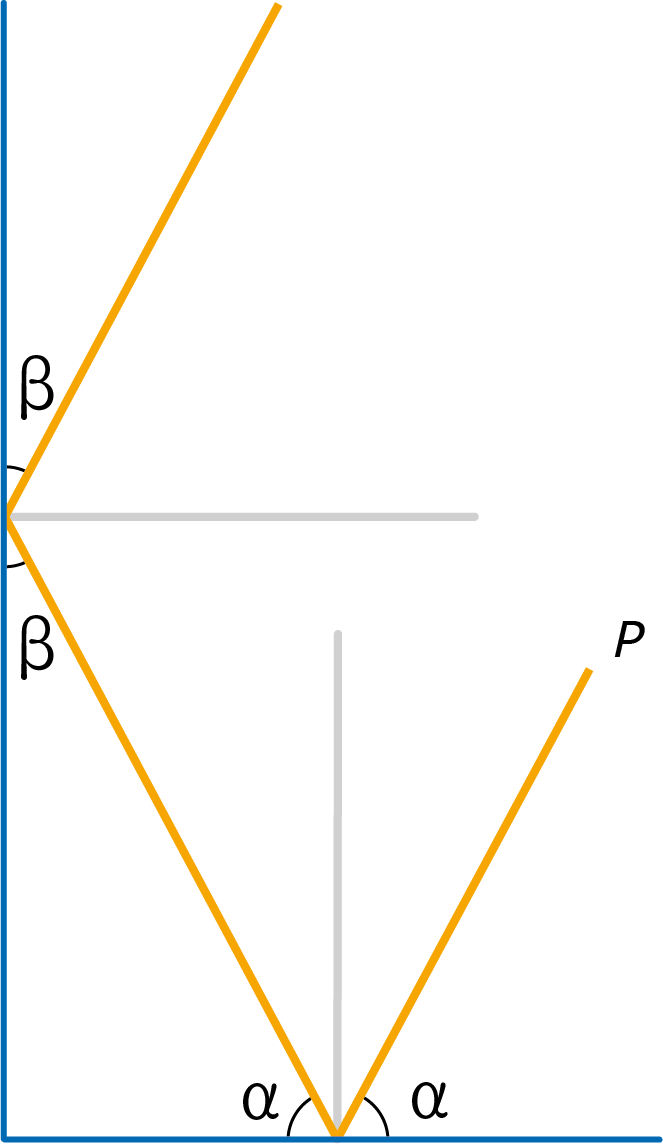
In figuur 2 zie je een situatie waarbij twee spiegels een hoek maken van $90^{\rm o}$. Wanneer iemand op de plek $P$ in de hoek schijnt, dan kaatst de lichtstraat eerst in de ene spiegel en daarna in de andere. Toon aan dat dan de teruggekaatste lichtstraat parallel is aan de invallende lichtstraal, onafhankelijk van de hoek van inval. Of de teruggekaatste lichtstraal parallel is aan de invallende lichtstraal hangt bij een hoek van $90^{\rm o}$ dus NIET af van de hoek van inval.

We maken de situatie nog iets ingewikkelder. Deze situatie lijkt op die van figuur 2 maar de hoek $\varphi$ tussen de twee spiegels is scherp, dat wil zeggen $0^{\rm o} \gt \varphi \gt 90^{\rm o}$. Iemand op plek $P$ schijnt weer de hoek in. De vraag is nu: bij welke hoeken $\alpha$ komt de uiteindelijk teruggekaatste lichtstraal parallel aan de invallende lichtstraal? En wat gebeurt er als $\varphi$ stomp is ($\varphi \gt 90^{\rm o}$)?

Je zult vinden dat alleen bij bepaalde speciale hoeken $\varphi$ de teruggekaatste lichtstraal parallel kan zijn aan de invallende lichtstraal. Maar sommige van die hoeken $\varphi$ zijn nog niet iets specialer dan andere. Je hebt namelijk twee soorten. Bij de ene soort kan de teruggekaatste lichtstraal parallel zijn aan de invallende lichtstraal, maar dat is alleen zo bij één bepaalde invalsrichting. Dat zagen we al eerder, bij figuur 1. Bij de andere soort is de teruggekaatste lichtstraal altijd parallel aan de invallende lichtstraal. Dat zagen we bij figuur 2.

Oplossing

We bekijken eerst figuur 3. Daarin wordt een invallende straal eerst onder hoek $\alpha$ teruggekaatst, vervolgens onder een hoek $\beta$, dan hoek $\gamma$ en ten slotte hoek $\delta$. Met $\varphi$ duiden we de hoek aan tussen de twee spiegels. Verder is gegeven dat de inkomende straal parallel is aan de uitgaande straal. Wat kan er worden gezegd over $\varphi$?

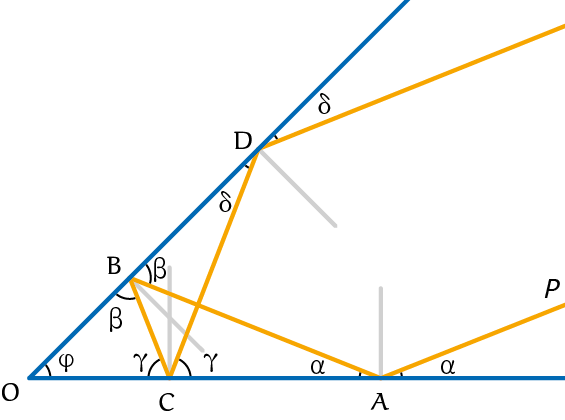
De som van de drie hoeken in een driehoek is $180^{\rm o}$. Daarnaast is de som van de hoeken bij een punt eveneens $180^{\rm o}$. Zo geldt voor de driehoek $OAB$ dat $\alpha + \varphi + 180^{\rm o} - \beta = 180^{\rm o}$. We vinden dat $\beta = \alpha + \varphi$. De andere relaties die we vinden zijn: $\beta + \gamma + \varphi = 180^{\rm o}$ en $\delta + \varphi = \gamma$.

Het gegeven dat de inkomende straal parallel is aan de uitgaande straal kan worden vertaald in $\alpha + \delta = \varphi$. Dit combineren we met bovenstaande. $\delta = \varphi - \alpha = \gamma - \varphi = 180^{\rm o} - 2\varphi - \beta = 180^{\rm o} - 3\varphi - \alpha$. Nu valt $\alpha$ weg uit de vergelijking en we houden over $4\varphi = 180^{\rm o}$, ofwel $\varphi = 45^{\rm o}$. 

In principe kan elk volgend geval op deze manier worden opgelost, maar het kan wat efficiënter.

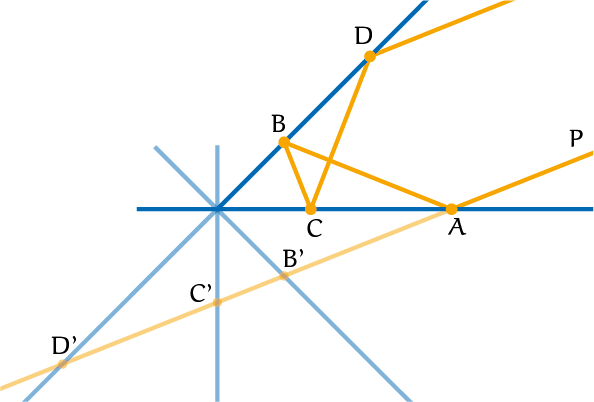
Daarvoor kijken we naar figuur 4. Je moet je voorstellen dat er een wereld bestaat achter de spiegel. De lichtstraal gaat dan rechtdoor in de virtuele wereld achter de spiegel. In deze wereld botst de lichtstraal opnieuw tegen een spiegel aan (bij $B'$). Dan kun je je ook voorstellen dat er achter deze virtuele spiegel opnieuw een virtuele wereld bestaat. In die wereld reist de lichtstraal door naar $C’$. Daarachter is weer een andere wereld en reist de lichtstraal naar $D’$. Achter $D’$ reist de lichtstraal verder. De punten $B’$, $C’$ en $D’ $corresponderen in de echte wereld met $B$, $C$ en $D$. De voorwaarde dat de inkomende straal parallel is aan de uitgaande straal betekent dat $D$, $S$ en $D’$ op één lijn liggen, waarbij $S$ het snijpunt is van de twee spiegels. Immers als deze drie punten niet op één lijn liggen, dan zijn de lijnen $AD’$ en de lijn door $D$ niet parallel. Omdat de hoek tussen de spiegels steeds gelijk is in de virtuele wereld, vind je dat viermaal deze hoek $180^{\rm o}$ moet zijn. De hoek tussen de twee spiegels is $45^{\rm o}$.

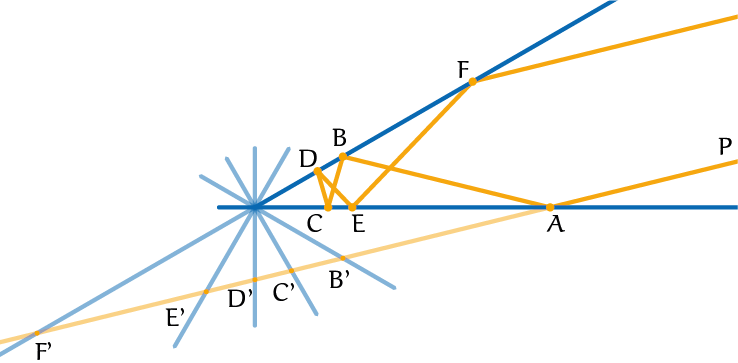
Het voorbeeld in figuur 5 behoeft weinig toelichting. De hoek tussen de twee spiegels herhaalt zich zesmaal. Deze som van zes hoeken is $180^{\rm o}$. De hoek moet dus $30^{\rm o}$ zijn.