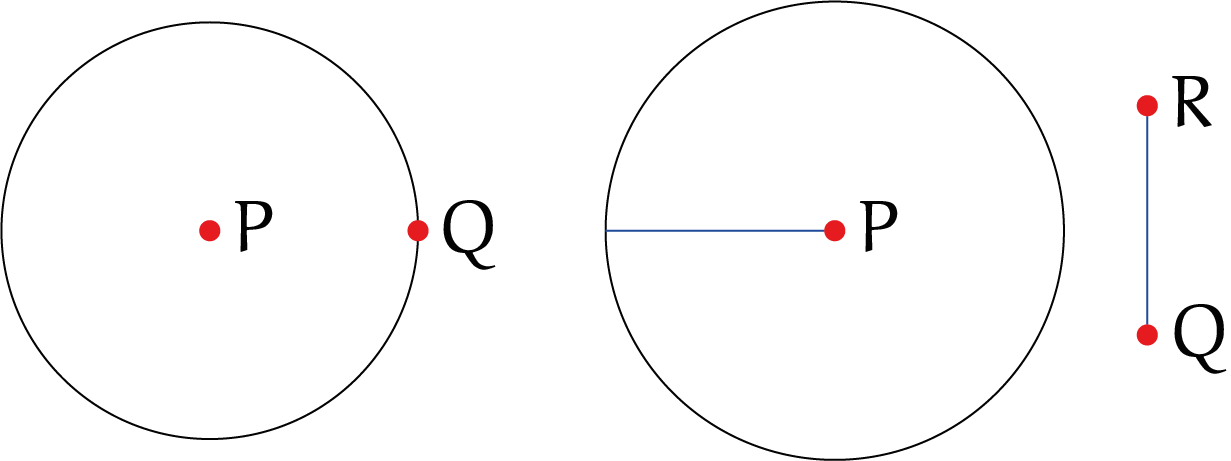
Met een passer kunnen we uiteraard cirkels maken. Dit kan op twee manieren. We laten ze zien in figuur 1, want de notatie die we hier gebruiken is handig in het vervolg van de puzzel.

1. Punten $P$ en $Q$ zijn gegeven. We kunnen dan een cirkel construeren door $Q$ met middelpunt $P$. Notatie voor deze cirkel: $P(Q)$.
2. Punten $P$, $Q$, $R$ zijn gegeven. We kunnen een cirkel construeren met middelpunt $P$ en straal de afstand tussen $Q$ en $R$. Notatie voor deze cirkel: $P(QR)$.

Vanuit oude punten kunnen we nieuwe punten construeren, namelijk als snijpunt van cirkels. Door dat te herhalen krijg je steeds meer punten. Welke punten kun je op deze manier maken? Deze vraag is de kern van deze puzzel.

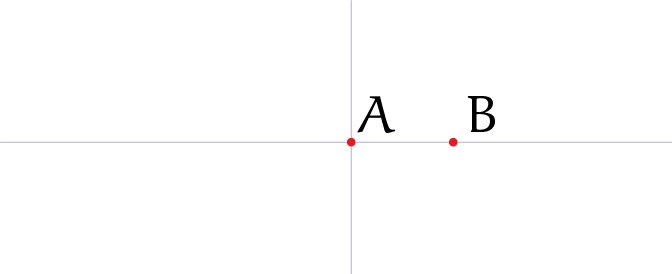
We beginnen in figuur 2 simpel, met twee verschillende punten, $A$ en $B$. Die punten beschouwen we als gegeven. Als we gebruik maken van coördinaten dan kunnen we deze coördinaten zo kiezen dat $A = (0, 0)$ en $B = (1, 0)$. Dus $B$ ligt 'rechts' van $A$, en hun onderlinge afstand is $1$.

Construeren van (2,0)

Opgave 1 Kunnen we het punt $(2, 0)$ construeren, startend vanuit $A$ en $B$, met alleen een passer? (Hint: er zijn verschillende mogelijkheden.)

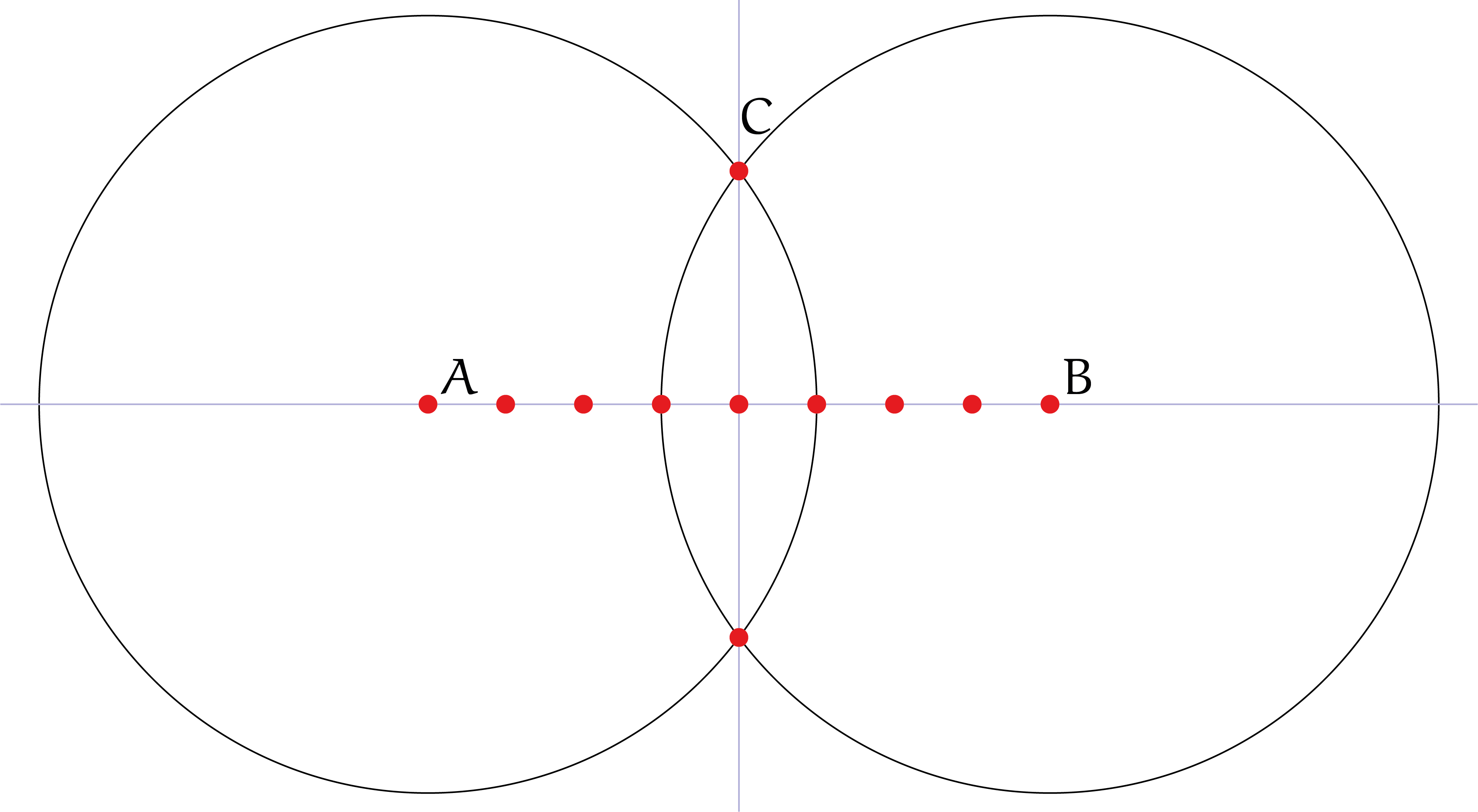
Ja. Zie figuur 3. Laat $C$ een van de snijpunten zijn in de doorsnede van de twee cirkels $A(B)$ en $B(A)$. Kies D als snijpunt van $B(C)$ en $C(B)$ het verst weg van $A$. Construeer $E$ als het nieuwe snijpunt van $D(B)$ en $B(D)$ (niet zijnde $C$). $E$ is het punt $(2, 0)$.

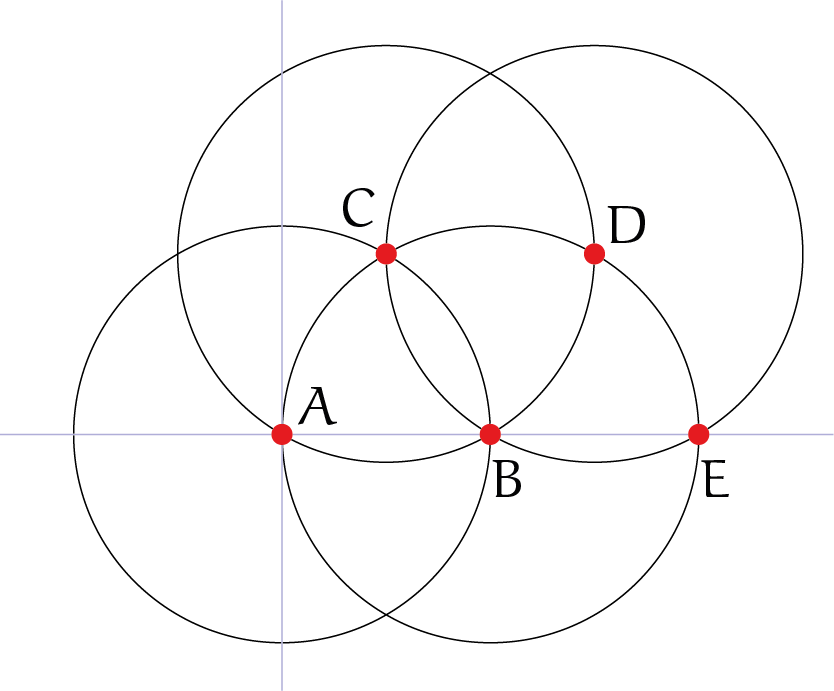
Zo doorgaand met deze driehoeksconstructie kun je zes punten maken die een regelmatige $6$-hoek vormen om het middelpunt $B$.

Gevolg: door voortdurende herhaling van deze constructie ‘naar rechts’ kunnen we alle punten $(n, 0)$ maken met n positieve gehele getallen.

Gevolg: door dezelfde constructie naar links uit te voeren kunnen we alle $(n, 0)$ met $n < 0$ construeren.

Gevolg: dus nu hebben we feitelijk alle punten $(n, 0)$ geconstrueerd, met $n$ een geheel getal, uitgaande van $0$ en $1$, met enkel een passer.

Construeren van (0, 1)

Nu een stap verder. Kunnen we nu ook $(0, 1)$ construeren? Dat is nog niet vanzelfsprekend. Ga na dat $(0, \sqrt{3})$ makkelijk te construeren is via de driehoeksconstructie die we hierboven zagen, zoals in figuur 3. Maar daarmee hebben we nog niet $(0, 1)$.

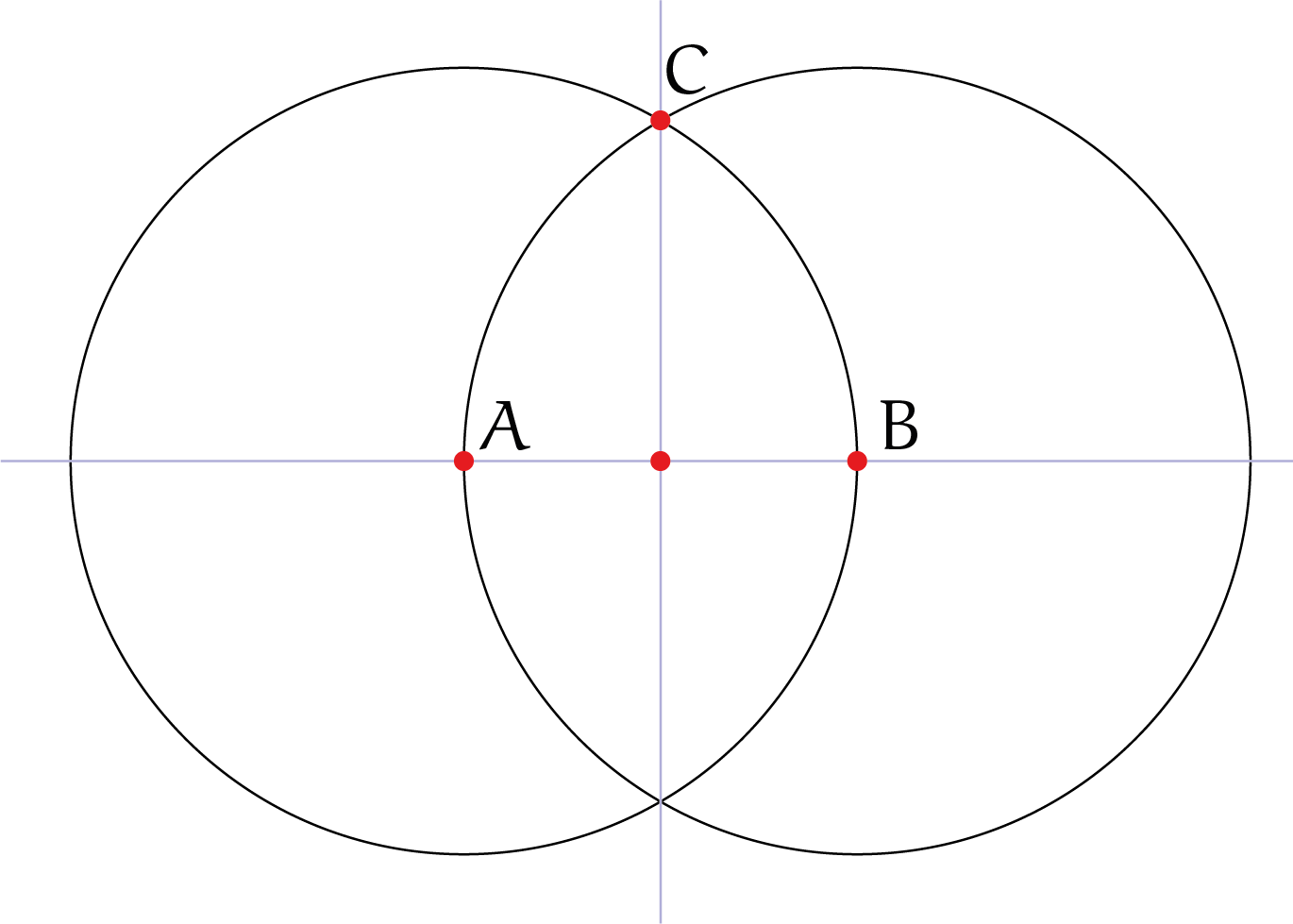
Om $(0, -1)$ te construeren kunnen we het volgende doen:

Stap 1 Gebruik twee cirkels met straal $5$ en middelpunten $(-4, 0)$ en $(4, 0)$, figuur 5. Die kunnen we construeren, zoals we hierboven gezien hebben en ook de lengte $5$ kunnen we construeren. De twee cirkels snijden elkaar in twee punten, $(0, 3)$ boven en $(0,-3)$ onder $(0, 0)$.

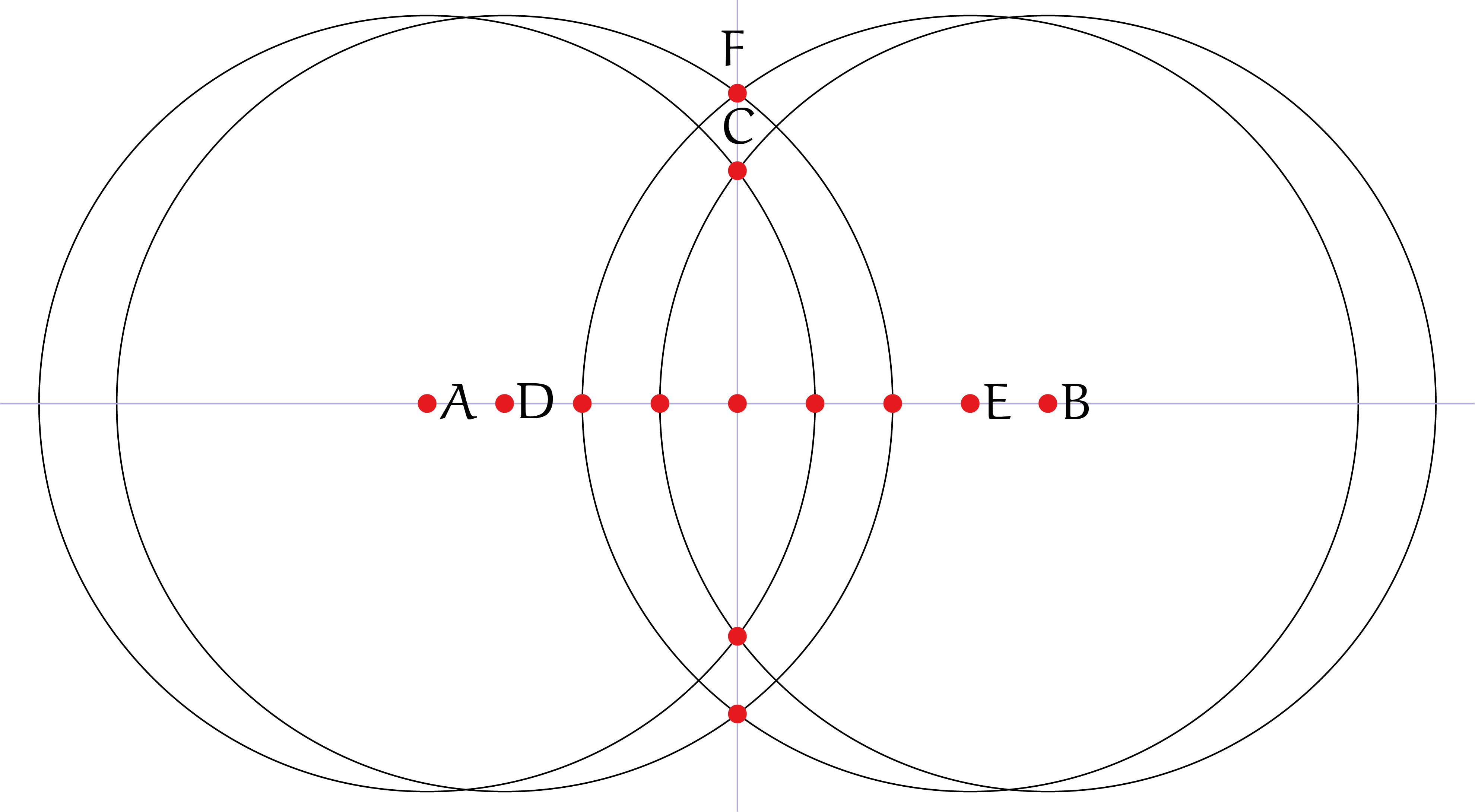
Stap 2 Gebruik opnieuw de straal $5$, maar nu samen met de twee punten $(-3, 0)$ en $(3, 0)$. Nu kunnen we $(0, 4)$ en $(0, -4)$ construeren
in figuur 6.

Stap 3 Vanuit $(0, 4)$ via $(0, 3)$ kan $(0, 2)$ worden geconstrueerd met een constructie zoals in figuur 3. En uit $(0, 3)$ en $(0, 2)$ kunnen we $(0, 1)$ construeren. Zie figuur 7.

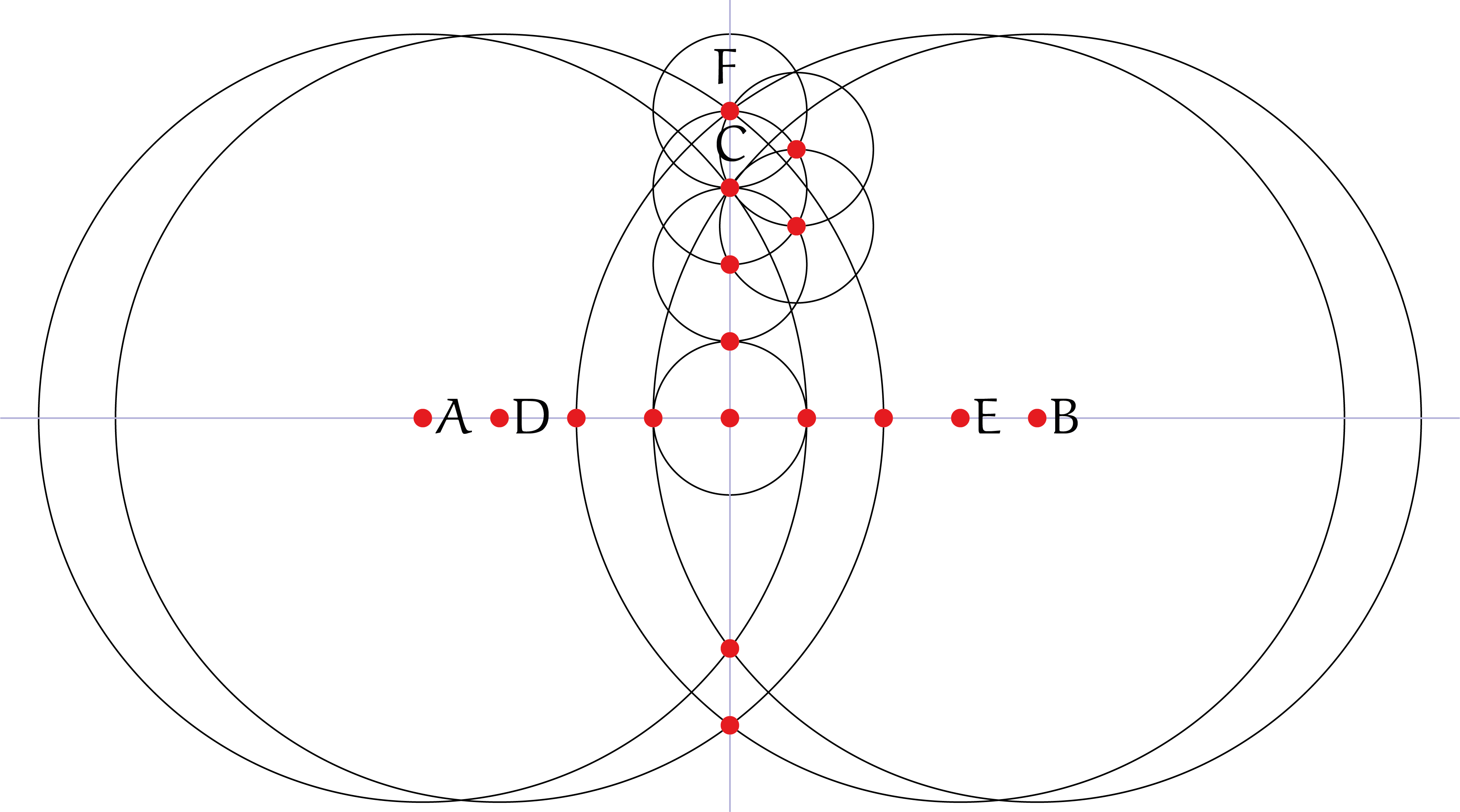
Gevolg: omdat $(0, 1)$ kan worden geconstrueerd, kunnen alle punten $(0, n)$ met $n$ een geheel getal worden geconstrueerd, met de driehoeksconstructie van hierboven.

Opgave 2 Bovengenoemde constructie is best nog ingewikkeld. Kun jij een simpelere constructie bedenken (dus een constructie waarbij je minder cirkels hoeft te tekenen). Je moet niet bang zijn om niet gehele lengtes te gebruiken!

 

Opgave 3 Laat zien dat $(m, 1)$ kan worden geconstrueerd uit $(m, 0)$ en $(m+1, 0)$.

 

Opgave 4 Laat zien dat $(m, n)$ kan worden geconstrueerd uit $(0, 0)$, $(m, 0)$ en $(0, n)$.

Gevolg: alle roosterpunten $(m, n)$ (met $m, n$ geheel) kunnen worden geconstrueerd.

Bonusvraag Kun je $(\frac{3}{7}, 0)$ construeren

Misschien wil je eerst zelf iets uitproberen. Lees dan niet verder.

 

Het is mogelijk maar niet zo simpel. Online kun je eens kijken naar de stelling van Mohr-Mascheroni en de bijbehorende constructies met passer zonder liniaal. Met die Mohr-Mascheroniconstructies lukt het je wel.

Bonusvraag Construeer $(\sqrt{ab},0)$ uit $(a,0)$ en $(b,o)$,

 

Bonusvraag Stel je nu voor dat je een hele oude passer tot je beschikking hebt, waarvan de benen op een vaste afstand van elkaar staan. Je hebt opnieuw de punten $(0, 0)$ en $(1, 0)$. Kun je nu $(0, 1)$ construeren? Nou, in het algemeen gaat dat je niet lukken. Maar in een aantal gevallen zal het je wel lukken! Kun jij nagaan aan welke voorwaarde de afstand van de benen moet voldoen om de constructie mogelijk te maken?