Voor we deze kromme gaan bekijken moeten we even afspreken wat we eigenlijk met een kromme bedoelen. Dat was in de tijd van Peano en Von Koch niet helemaal duidelijk. Dat wil zeggen, eerst leek het duidelijk: een lijntje dat je met je potlood op papier tekent. Maar toen men er wiskundig mee moest gaan werken bleek dat geen goede definitie (of eigenlijk: helemaal geen definitie). 

Een van de pogingen tot definitie was: iets wat je met een continue functie van $[0, 1]$ (of een ander interval) naar $\mathbb{R}^2$ kunt beschrijven. Zoals een cirkel; die kun je beschrijven met behulp van het interval $[0, 2\pi]$ en de functie $t \mapsto \left(\cos(t), \sin(t)\right)$.

Echter, weer vijftien jaar eerder, in 1875, had Karl Weierstraß een continue functie beschreven die in geen enkel punt differentieerbaar is; de grafiek van die kromme voldoet aan deze definitie maar is niet zo makkelijk met een potlood te tekenen.

En in 1890 kwam Peano dus met een functie $t \mapsto (x(t), y(t))$ op de proppen die helemaal niet met een potlood te volgen is: elk punt in het vierkant ligt op die kromme. Je kunt dat vierkant helemaal volkleuren, maar dat is niet hetzelfde als de kromme van Peano volgen.

De kromme

Het artikel van Peano is makkelijk te vinden via https://eudml.org/doc/157489. Als je het leest dan zul je zien dat er geen enkel plaatje getekend wordt; Peano beschreef zijn functie $f$ volledig algebraïsch. Toch kun je wel plaatjes bij de definitie tekenen. Als je namelijk de berekeningen van Peano volgt voor $0$ en $1$ dan zie je dat $f(0) = (0, 0)$ en $f(1) = (1, 1)$. Je kunt dat interpreteren als het plannen van een reis: we beginnen in $(0, 0)$ en we eindigen in $(1, 1)$:

In het artikel van Peano wordt met ontwikkelingen in basis $3$ gewerkt; niet met decimalen dus. De 'cijfers' van een reëel getal $t$ in $[0, 1]$ kunnen $0, 1$, of $2$ zijn en als we $t = 0{,}t_1t_2t_3t_4\ldots$ schrijven dan bedoelen we $t = t_1 \cdot 3^{-1} + t_2 \cdot 3^{-2} + t_3 \cdot 3^{-3} + t_4 \cdot 3^{-4} + \cdots$ Dus $\tfrac{1}{3} = 0{,}1000\ldots$,  $\tfrac{2}{3} = 0{,}2000\ldots$, $\tfrac{1}{9} = 0{,}0100\ldots$, $\tfrac{4}{9} = 0{,}1100\ldots$, $\tfrac{8}{9}=0{,}2200\ldots$, enzovoort.

Als je berekeningen van Peano loslaat op $\tfrac{1}{9}$ tot en met $\tfrac{8}{9}$ dan krijg je de punten $(\tfrac{1}{3}, \tfrac{1}{3}), (0, \tfrac{2}{3}), (\tfrac{1}{3}, 1), (\tfrac{2}{3}, \tfrac{2}{3}), (\tfrac{1}{3}, \tfrac{1}{3}), (\tfrac{2}{3}, 0), (1, \tfrac{1}{3}), (\tfrac{2}{3}, \tfrac{2}{3})$ (in die volgorde). Daar zien we dat we onze route wat aanpassen tot de volgende rondreis door het vierkant in figuur 2 (hoe verder in de tijd, hoe minder rood en meer blauw):

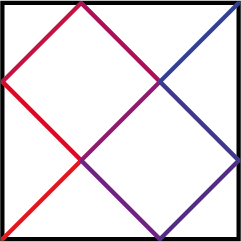
Je ziet dat we de punten $(\tfrac{1}{3},\tfrac{1}{3})$ en $(\tfrac{2}{3},\tfrac{2}{3})$ twee keer bezoeken. Je ziet wellicht aankomen wat de volgende aanpassing van het reisplan wordt: we gaan elk van de negen diagonalen vervangen door rondreisjes in de bijbehorende vierkantjes. Het wordt veel werk, maar voor elke breuk $\tfrac{k}{81} (k = 1, \ldots , 80)$ bepalen we weer wat Peano's recept oplevert (niets nieuws voor $\tfrac{t}{9} = \tfrac{9t}{81})$ en als we die punten plotten en verbinden krijgen we de route in figuur 3.

Probeer zelf de volgorde en richtingen maar eens aan te geven waarin we deze route volgen (natekenen op een groter stuk papier helpt).

In de volgende stap nemen we alle breuken met noemer $9^3 = 729$ en dan wordt dit onze reis:

Er gebeuren hier twee dingen: de reisroutes komen steeds dichter bij elk punt en de aanpassingen van de routes zijn steeds kleiner.

Met het eerste plan is de afstand tussen een willekeurig punt en het pad maximaal $\tfrac{1}{2}\sqrt{2}$; het tweede brengt de afstand terug tot $\tfrac{1}{2}\sqrt{2}\cdot 3^{-1}$, het derde maakt daar $\tfrac{1}{2}\sqrt{2}\cdot 3^{-2}$ van en bij het vierde wordt dat $\tfrac{1}{2}\sqrt{2}\cdot 3^{-3}$.

In het algemeen: als we alle breuken met noemer $3^{2k}$ gebruiken dan ligt elk punt niet verder dan $\tfrac{1}{2}\sqrt{2}\cdot 3^{-k}$ van de bijbehorende kromme vandaan.

Het tweede is dat we, telkens als we het $k$-de reisplan aanpassen en daar het $k+1$-ste plan van maken, nooit meer dan $\tfrac{1}{2}\sqrt{2}\cdot 3^{-k}$ van het $k$-de plan afwijken. Kijk maar naar de plaatjes: het volgende plan houdt ons in het vierkantje waar we eerst diagonaal doorheen reisden.

De gevolgen van die twee dingen zijn: onze reisplannen convergeren naar een reisplan dat bij een continue reis hoort én dat limietreisplan bezoekt echt elk punt in het vierkant (en sommige punten, zoals $(\tfrac{1}{3},\tfrac{1}{3})$, meer dan één keer).

Het bewijs van die gevolgen vergt een beetje wiskunde uit een eerstejaarscollege Analyse, dus dat slaan we hier over.

Nu vraag je je misschien af hoe die berekeningen van Peano er uitzien.

Eigenlijk heb je die niet nodig. Je kunt namelijk de reisroutes die we hier geschetst hebben zelf verder maken. De eerste stap laat zien hoe je elk diagonaaltje van een vierkant moet aanpassen om de volgende route te maken: verdeel het interval in negen stukken en loop via het eerste patroon door het vierkant; bij ieder volgend vierkant draai je het patroon zodat de begin- en eindpunten op de juiste plaats liggen.

Maar voor wie nieuwsgierig is geven we hieronder aan hoe Peano te werk ging.

Rekenen als Peano

Peano was voorzichtig. Je kunt wel inzien waarom: net zoals je $\tfrac{1}{2}$ op twee manieren in decimalen kunt schrijven, $0{,}5000\ldots$ en $0{,}4999\ldots$, kun je $\tfrac{1}{3}$ en vele andere breuken met een macht van $3$ in de noemer op twee manieren in het drietallig stelsel opschrijven: $0{,}1000\ldots$ en $0{,}0222\ldots$.

Peano moest bij elke $t \in [0, 1]$ een punt $(x(t), y(t))$ in het vierkant maken, dat zijn dus twee getallen in $[0, 1]$. In eerste instantie keek hij alleen naar rijen drietallige cijfers; hij schreef $T = 0{,}t_1t_2t_3\ldots$ (en waarschuwde: het is slechts een rij cijfers!). Van zo’n rij maakte hij twee rijen, op een heel speciale manier.

Ten eerste voerde hij de operatie 'omkeren' in: $k(0) = 2$, $k(1) = 1$ en $k(2) = 0$; dat keert dus het rijtje $(0, 1, 2)$ om tot $(2, 1, 0)$. Dat lijkt niet zo ingewikkeld en dat is het ook niet, maar Peano ging de operatie herhalen: $k^n$ staat voor het $n$ keer uitvoeren van $k$. Als je even nadenkt zie je dat $k^n$ niets doet als $n$ even is, en alles omdraait als $n$ oneven is, nog steeds niet erg opwindend. En verder blijft $1$ altijd op zijn plaats.

Maar Peano gebruikte dit bij het maken van de twee rijen, $X$ en $Y$, uit $T$.

$x_1=t_1$		$y_1=k^{t_1}(t_2)$
$x_2=k^{t_2}(t_3)$		$y_2=k^{t_1+t_3}(t_4)$
$x_3=k^{t_2+t_4}(t_5)$		$y_3=k^{t_1+t_3+t_5}(t_6)$
$x_n=k^{t_2+t_4+\cdots+t_{2n-2}}(t_{2n-1})$
$y_n=k^{t_1+t_3+\cdots+t_{2n-1}}(t_{2n})$

De voorgaande cijfers $t_i$ bepalen dus telkens hoe de cijfers $t_{2n-1}$ en $t_{2n}$ omgekeerd worden. Laten we dit op $T = 0{,}0100\ldots$ loslaten. Dan krijgen we $x_1 = 0$, $y_1 = k^0(1) = 1$, $x_2 = k^1(0) = 2$, $y_2 = k^0(0) = 0$, $x_3 = k^1(0) = 2, \ldots$. Je ziet dat $X = 0{,}0222\ldots$ en $Y = 0{,}1000\ldots$ gaan worden.

Nu hoort deze $T$ bij $t = \tfrac{1}{9}$, maar de rij $S = 0{,}00222\ldots$ hoort ook bij $t = \tfrac{1}{9}$. Als we het recept op $S$ toepassen krijgen we rijen $U$ en $V$ met $u_1 = 0$, $v_1 = k^0(0) = 0$, $u_2 = k^0(2) = 2$, $v_2 = k^2(2) = 2$, $u_3 = k^2(2) = 2$, $v_3 = k^4(2) = 2, \ldots$. Dat levert dus $U = 0{,}0222\ldots$ en $V = 0{,}0222\ldots$ op.

Als we echter van die rijen de bijbehorende getallen opschrijven krijgen we $x = \tfrac{1}{3}$ en $y = \tfrac{1}{3}$, maar ook $u = \tfrac{1}{3}$ en $v = \tfrac{1}{3}$.

We zien: ook al horen bij $\tfrac{1}{9}$ twee rijen cijfers, de twee paren die we er mee maken horen bij hetzelfde punt, $(\tfrac{1}{3},\tfrac{1}{3})$, in het vierkant.

Daarom was Peano voorzichtig en liet hij eerst zien hoe uit één rij twee rijen te maken. En dat het recept omkeerbaar is: probeer maar uit de twee rijen cijfers $X$ en $Y$ de rij $T$ te reconstrueren. Het begint met $t_1 = x_1,$ $t_2 = k^{x_1}(y_1), \ldots$.

Daarna liet hij zien: als twee rijen $T$ en $S$ hetzelfde getal bepalen dan bepalen de twee bijbehorende paren rijen hetzelfde punt in het vlak. Zo kon hij ondubbelzinnig aan elk getal een punt in het vierkant toewijzen.

Daarna was het eigenlijk niet moeilijk na te gaan dat elk punt aan een getal werd toegewezen (elk punt wordt op de reis bezocht) en dat de toewijzing een continue functie was.

Ik denk overigens dat Peano stiekem op kladpapier plaatjes heeft getekend zoals degene die wij hierboven gezien hebben en dat hij aan de hand daarvan die formules heeft uitgedokterd. Maar bewijzen kan ik dat niet.