Mogelijk heb je jezelf al eens afgevraagd: Zit er een algoritme achter de volgorde van de familieleden in de banners? Op pyth.eu/series staan ze allemaal onder elkaar. Bij een wiskundige familie zal die volgorde geen toeval zijn; daar is vast over nagedacht.

Het eerste dat je kan opvallen is dat de volgorde niet telkens hetzelfde is. Sterker nog, ze verschillen allemaal (al is het bij het drukken wel een keer verkeerd gegaan). We noemen zo'n volgorde ook wel een permutatie. Met vier gezinsleden zijn er dan "vier faculteit" permutaties: $4! = 4 \times 3 \times 2 \times 1 = 24$. Dat betekent ook dat we met deze aflevering alle permutaties gehad hebben.

We zoeken dus een algoritme om die $24$ permutaties in een zekere volgorde onder elkaar te zetten. Dat kan op allerlei manieren.
Waarschijnlijk is de meest voor de hand liggende manier (zie figuur 1) om vier blokken van zes te maken, waarbij in elk blok één van de vier familieleden telkens vooraan staat. De drie andere familieleden staan in elk blok op zes verschillende volgordes: $3! = 3 \times 2 \times 1 = 6$. En dat kan in drie blokjes van twee, met één van de overige familieleden telkens op de tweede plaats. In het blokje van twee staan de laatste twee familieleden op beide volgordes op plaatsen drie en vier: $2! = 2 \times 1 = 2$. Dat is heel systematisch, zoals woorden in een woordenboek. We zeggen dan ook dat dit algoritme de permutaties in lexicografische volgorde produceert. Python heeft daarvoor zelfs een ingebouwde functie:  .

Maar het algoritme voor de banners werkt anders. Waarom zou je het anders doen? Ten eerste is de lexicografische volgorde wat saai. Aan de linkerkant verandert er niet zo vaak wat. Ten tweede verandert er soms erg veel van de ene op de volgende permutatie. Beschouw bijvoorbeeld de overgang tussen het tweede blok dat eindigt op $\varphi m\mu\pi$ en het derde blok dat begint met $\mu\pi\varphi m$. De $\varphi$ en $m$ schuiven twee plaatsen naar rechts en de $\mu$ en $\pi$ juist twee plaatsen naar links, een totaal van acht. De minimale verschuiving krijg je als je twee letters die buren zijn van plaats verwisselt. De vraag is echter of je alle permutaties zo kan ordenen dat er alleen buurwisselingen nodig zijn.

In de 17^e eeuw had men dit probleem al opgelost in het kader van "change ringing", waarbij men een aantal klokken in alle mogelijke volgordes achter elkaar wil luiden met alleen buurwisselingen (zoek daar maar eens naar op YouTube). Met maar drie letters is dat makkelijk: $ABC$, $ACB$, $CAB$, $CBA$, $BCA$, $BAC$. Merk op dat we met nog een buurwisseling zelfs weer terug bij het begin zijn. Eigenlijk heb je bij drie letters weinig keus, omdat er maar twee buurparen zijn. Als je het ene paar net hebt gewisseld, moet je daarna het andere paar wisselen (want anders krijg je geen nieuwe permutatie). Maar bij vier letters zijn er drie buurparen en wordt het kiezen lastig.

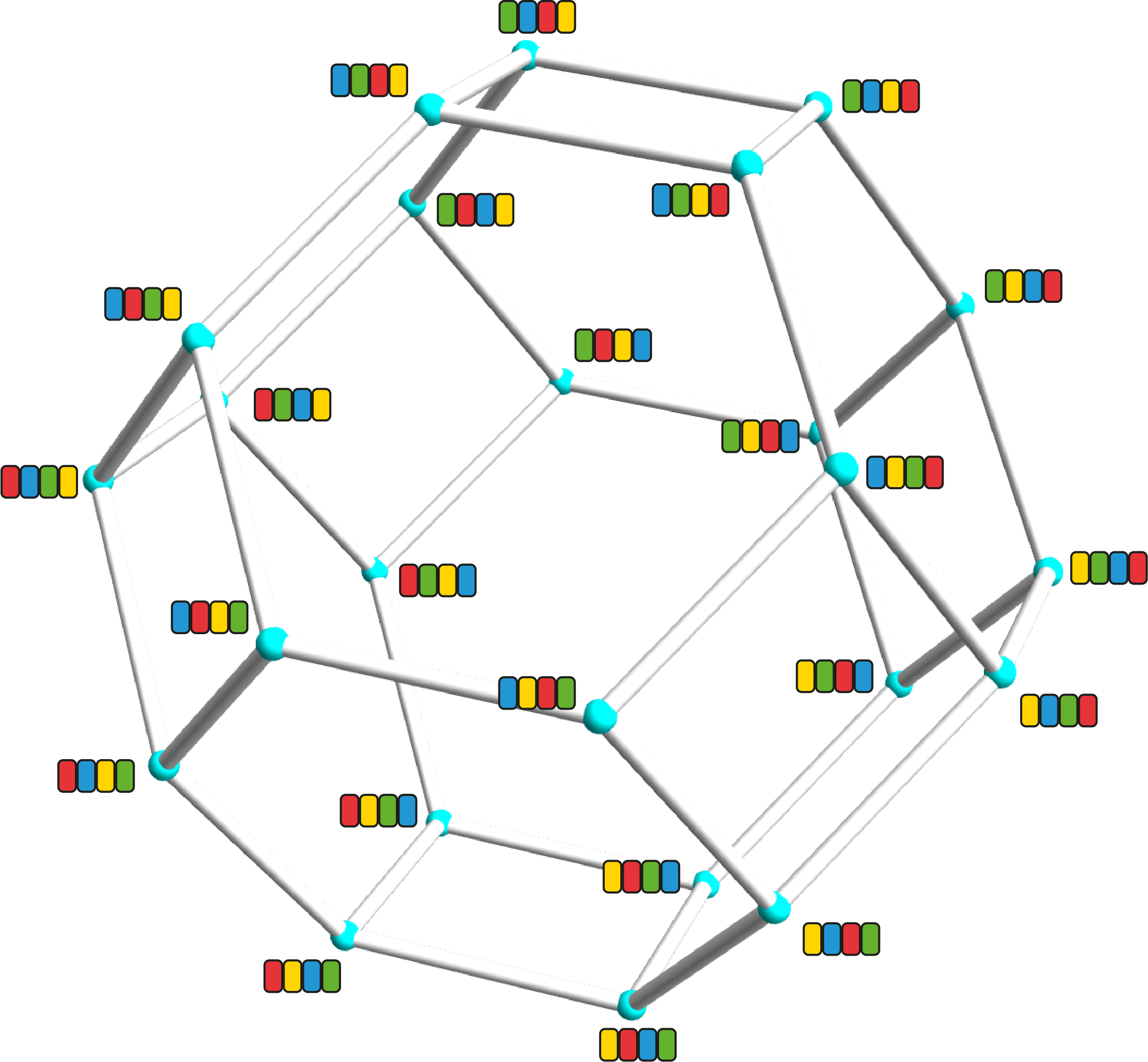
Je kunt een landkaart (graaf) maken met de permutaties als steden (knopen) en een weg (kant) tussen twee steden als de bijbehorende permutaties een buurwisseling verschillen. We noemen dat kortweg de buurwisselgraaf. Voor drie letters ziet die graaf er uit als een zeshoek en voor vier letters als een afgeknotte octaëder (ook wel permutohedron genoemd; zie figuur 2). Het kiezen van een volgorde van de permutaties met alleen buurwisselingen komt overeen met het vinden van een pad in de buurwisselgraaf, langs de kanten, dat elke knoop precies één keer bezoekt. Zo'n pad wordt wel een Hamiltonpad genoemd. Voor vier letters kun je nu vast wel zo'n Hamiltonpad vinden (zie figuur 3).

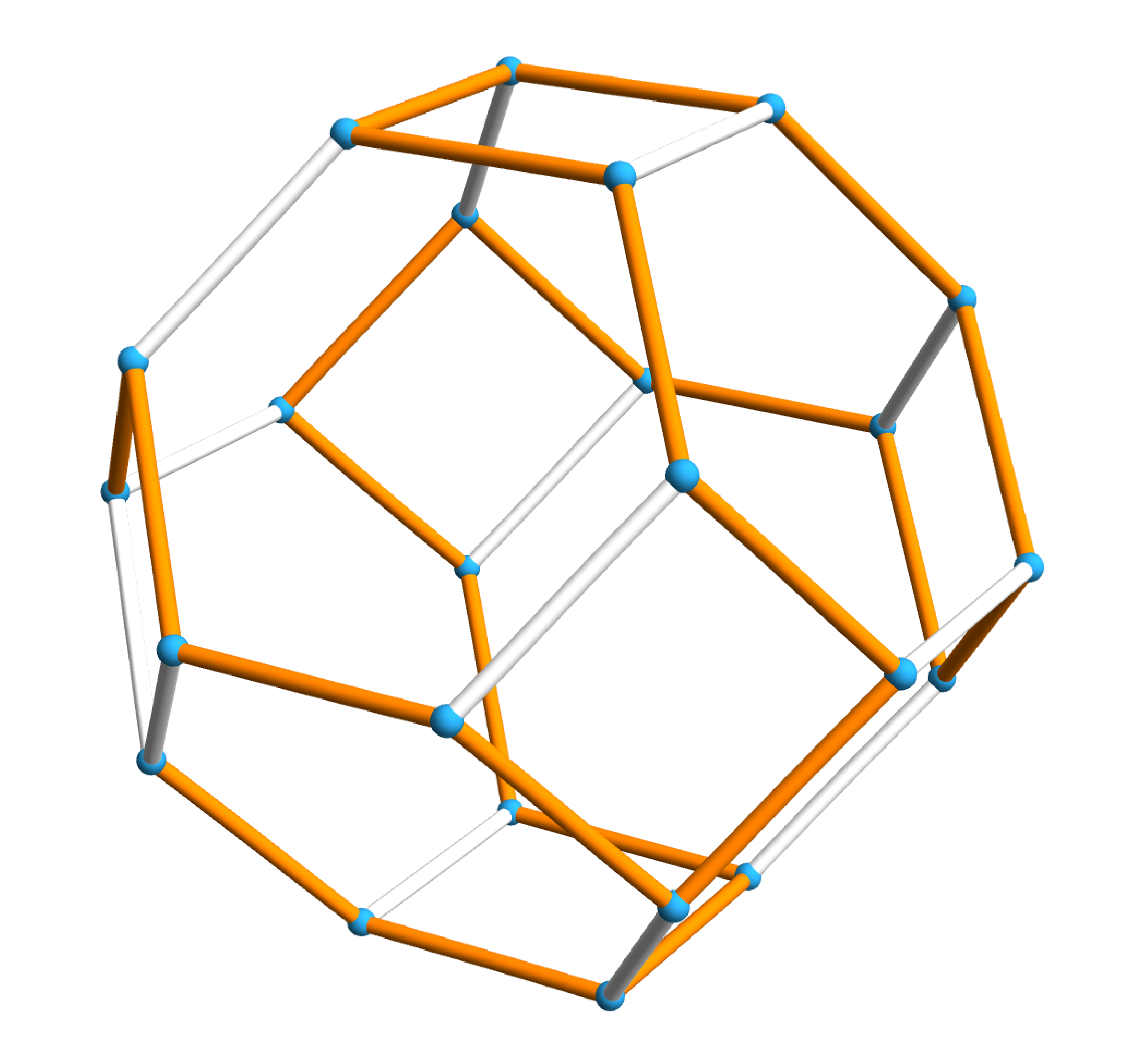
Het algoritme dat familie Van der Torus gebruikt heeft, vindt een bijzonder Hamiltonpad en werkt ook bij meer letters. Met drie letters, zeg $ABC$, is het makkelijk. Stel er komt nu een $D$ bij, dan kun je als volgt de $24$ permutaties met alleen buurwisselingen maken. $D$ begint helemaal rechts: $ABCD$. Drie opeenvolgende buurwisselingen met $D$ levert achtereenvolgens $ABDC$, $ADBC$ en $DABC$. $D$ heeft op elke positie gestaan waarbij $A$, $B$ en $C$ in dezelfde volgorde blijven staan. Nu staan $ABC$ weer naast elkaar en kunnen we met één buurwisseling hun volgorde veranderen: $DACB$.

Vervolgens wisselt $D$ hier weer in drie stappen doorheen naar rechts: $ACBD$. Aangezien $D$ telkens aan een uiteinde staat kunnen we $ABC$ met buurwisselingen op alle mogelijk manieren permuteren. Omdat $D$ op elke plaats met elk van de zes volgordes van $ABC$ heeft gestaan, hebben we precies de $24$ permutaties van $ABCD$ geproduceerd. Ik denk dat je nu zelf ook wel inziet hoe je er een vijfde letter $E$ bij kan betrekken om $120$ permutaties middels buurwisselingen te maken. Bovenstaande uitleg is nog geen algoritme dat een computer kan uitvoeren. Daartoe moeten we het in duidelijkere stappen opdelen. Dat kan als volgt. Bij elke letter zetten we een pijl die naar links of naar rechts wijst.

Stap 1. Het algoritme begint met alle letters op volgorde ($ABCD$) en alle pijlen naar links (<<<<).

Stap 2. Een letter waarnaast in de richting van diens pijl een lagere letter (eerder in het alfabet) staat, noemen we mobiel. Bepaal de hoogste letter (laatst in het alfabet) die mobiel is. Als zo'n letter er niet is, dan is het algoritme klaar. In het begin zijn $B$, $C$ en $D$ mobiel en is $D$ de hoogste.

Stap 3. Verwissel de hoogste mobiele letter met de buur in de richting van diens pijl.

Stap 4. Draai alle pijlen van hogere letters om. Herhaal vanaf Stap 2.

Deze beschrijving van het algoritme kan eenvoudig geprogrammeerd worden in Python (onder de knop [Bekijk oplossing] vind je de code in kopieerbaar formaat). We gaan uit van een lijst met $n$ verschillende letters en coderen een pijl naar links met –1 en een pijl naar rechts met 1. De functie maakt een lijst met bij elke letter een pijl naar links; we noemen zo'n lijst met pijlen een toestand:

De functie haalt alle pijlen weg uit een toestand:

In een toestand, is de letter op index met pijl mobiel als een index is, d.w.z. , en de letter op index kleiner is dan . Dit wordt bepaald in functie :

De functie bepaalt de indexen van alle mobiele letters:

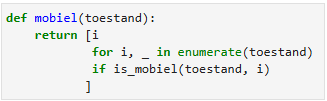
De functie  verwisselt de letter op index met de buur volgens diens pijl:

Het draaien van alle pijlen van grotere letters dan de letter op plaats gaat met de functie :

Tot slot kunnen we deze functies samen gebruiken om alle permutaties middels buurwisselingen af te drukken:

Hierbij gebruiken we de standaardfunctie die een i in m bepaalt waarvoor maximaal is. Dat is dus de index van de hoogste mobiele letter.

De permutaties van $ABCD$ worden nu afgedrukt met .

Hoe zijn de permutaties in de banners gegenereerd? Om de volgorde daarvan te krijgen beginnen we met de volgorde van de familieleden boven dit artikel $\pi\varphi\mu m$ als $ABCD$. En dan zijn de $23$ volgende permutaties volgens het voorgaande algoritme de banners van afleveringen $1$ tot en met $23$. Als je de permutaties onder elkaar zet en dezelfde letters met een gekleurde lijn verbindt, waarbij je om en om over en onderdoor gaat bij het wisselen, dan krijg je een mooie vlecht (zie figuur 4). Dit is ook het pad aangegeven in de buurwisselgraaf (figuur 3). Als je dat pad rond sluit, krijg je de vorm van de wisseltrofee voor de Nederlandse Wiskunde Olympiade: een Hamiltoncykel op de hoekpunten van de afgeknotte octaëder.

Tot slot volgt hier nog een nieuwe uitdaging. Stel je hebt $N$ gelijke objecten, zeg allemaal rood, en daarnaast nog één gele en één blauwe. Dan zijn er $(N + 1)(N + 2) $permutaties. Voor welke $N$ kun je die permutaties middels buurwisselingen genereren? En zo dat kan, hoe? Kijk eens of je kunt ontdekken wat de structuur van de buurwisselgraaf is.

 

 

Bekijk oplossing