Puzzle Jamming 61-1
Zes puzzelmakers schotelen je in elk nummer een eigen type raadsel voor. De oplossing vind je onderaan via de knop [Bekijk oplossing]
Zes puzzelmakers schotelen je in elk nummer een eigen type raadsel voor.
w4kangoerOE
(w4kangoeroe.nl)
Vier identieke dozen zijn aan elkaar gelijmd om de vorm te krijgen die op de afbeelding wordt getoond.
Als je 1 liter verf nodig hebt om de buitenkant van zo'n doos te schilderen, hoeveel liter verf heb je dan nodig om de buitenkant van de verlijmde constructie te schilderen?
| A $2{,}5$ | B $3$ | C $3{,}25$ | D $3{,}5$ | E $4$ |
Sudoku
(Wil Schilders)
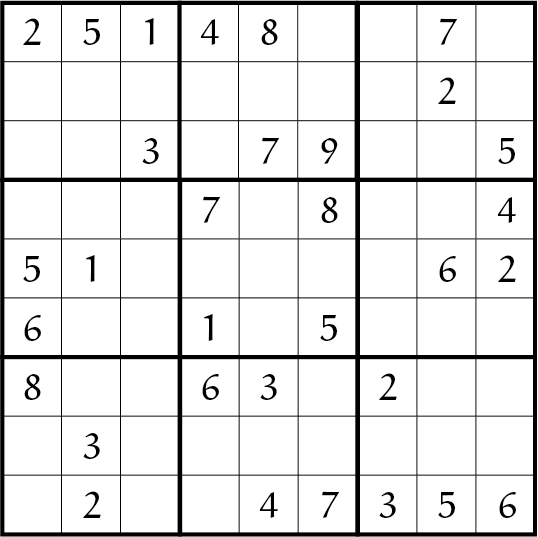
Op elke rij, in elke kolom en in elk $3\times3$ vlak moeten de cijfers $1$ t/m $9$ komen te staan. Deze puzzel is met logische stappen goed tot een einde te brengen.
De Sudoku's zullen in de volgende nummers steeds moeilijker worden!
Pen en papier
(Maarten Löffler)
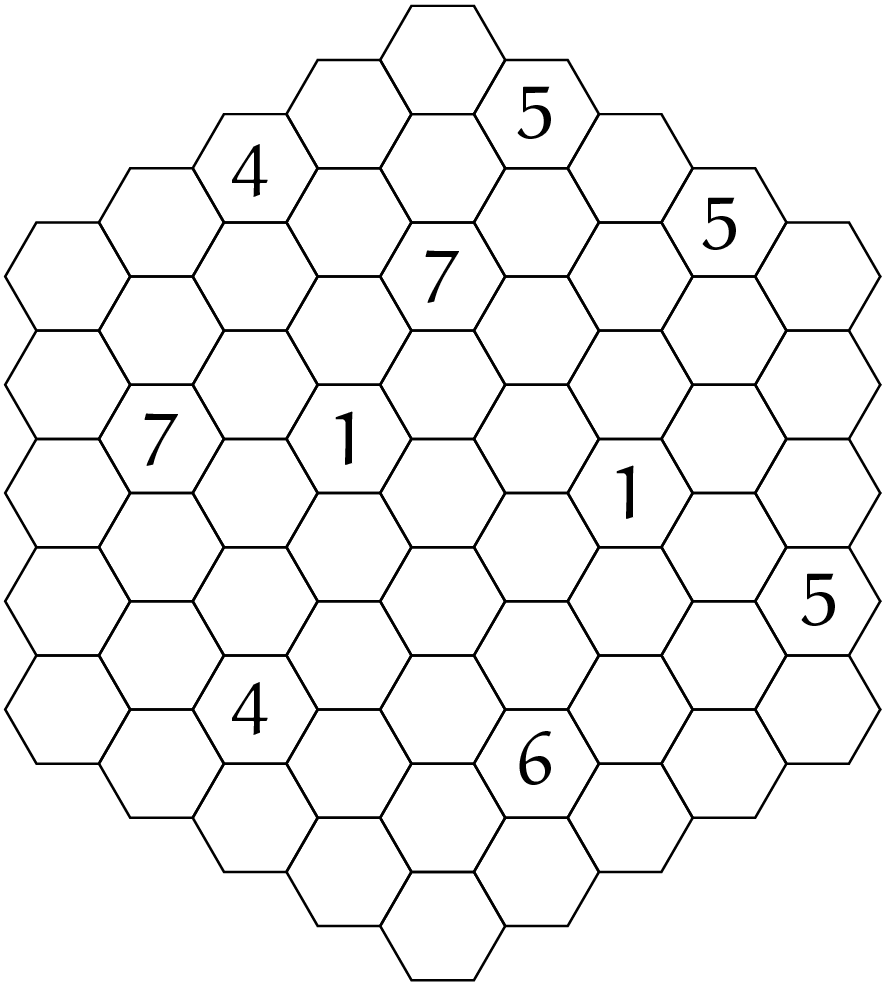
Dit eiland bestaat uit zeshoekige velden, en elk veld is laagland (hoogte $1$), heuvels (hoogte $2$), of gebergte (hoogte $3$). Het eiland is omgeven door zee (hoogte $0$). Aangrenzende velden kunnen hooguit een hoogteverschil van $1$ hebben en het hele eiland ligt boven zeeniveau. De cijfers in het diagram geven aan hoeveel andere velden zichtbaar
zijn vanaf dat veld in de zes hoofdrichtingen. Alleen velden die even hoog of lager liggen zijn zichtbaar, en een hoger liggend veld blokkeert de rest van de rij. Bepaal de hoogte van elk veld.
Priempropper
(Matthijs Coster)
In het diagram hieronder moeten geen cijfers maar priemgetallen van een of twee cijfers worden ingevuld. Let op: De $0$ komt dus niet voor. De komma laten we weg.
De beschrijvingen staan hieronder. Bij de beschrijving vul in $abc$ zó dat $a \times b = c$ kan bijvoorbeeld worden ingevuld $23\ 71\ 61$, immers $23 \times 7 = 161$. Zoals je ziet plak je de drie getallen achter elkaar en splits je ze op in $4$ priemgetallen.
- Vul in $abc$ zó dat $a + b = c$
- Datum van overlijden van beroemd surrealistisch schilder onder meer bekend van druipende horloges
- Palindroom
- Dalende rij van drie getallen
- $3^{\tfrac{3}{4}}$
- Driehoeksgetal ($1 + 2 + 3 + \cdots + k$)
- $\cos(44^{\rm o})$
- Kwadraat
Pentomino's
(Aad van de Wetering en Odette De Meulenmeester)
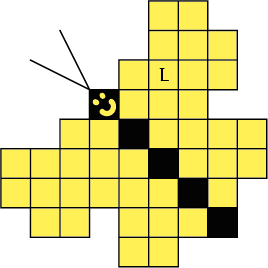
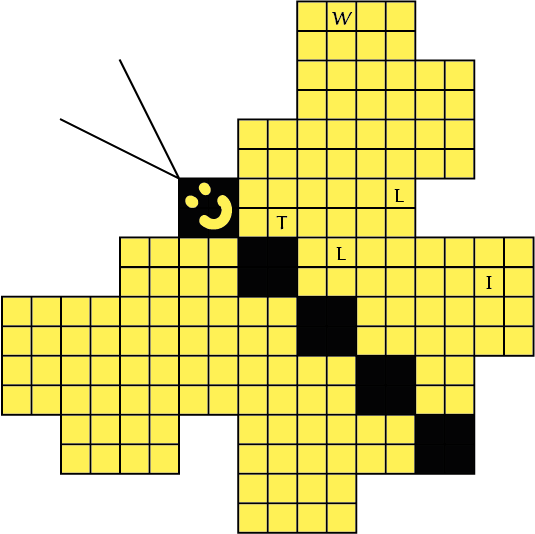
Hierboven staan alle pentomino's met hun letters. Vul de gele hokjes van de vlinders met pentomino's zodat geen twee pentomino's met dezelfde vorm (ook niet gedraaid of gespiegeld) een zijde gemeen hebben. Een vierkantje met een letter er in moet deel uitmaken van de pentomino met dezelfde naam.
Zorg dat de oplossingen een symmetrieas hebben. Merk op dat je viermaal zoveel pentomino's nodig hebt om de vlinder op schaal 2 te vullen.
