Pythagon nieuwjaarsopdracht uitslag
In het septembernummer schreven we de Pythagon-prijsvraag uit. Je kunt nog meedoen tot 10 april, maar voor de speciale nieuwjaarsopdracht was de deadline 1 januari. De fraaiste inzendingen bespreken we in dit artikel.
De brievenbus van de Pythagon-prijsvraag vulde zich, voornamelijk in december, met allerlei mogelijke inzendingen: filmpjes, knutselwerken en berekeningen. Een pythagon is een vierkant van 1 × 1 met twee keer daaraan vastgeplakt een gelijkbenige rechthoekige driehoek. Er bestaan zeven verschillende pythagons. De nieuwjaarsopdracht bestond uit drie vragen:
- Wat is de kleinste omtrek die je met 217 pythagons kan maken? Gebruik precies 31 keer de gehele verzameling van 7 pythagons (7 × 31 = 217).
- Wat is het kleinste aantal pythagons waarmee je een oppervlakte van 217 kan omcirkelen? De aantallen van verschillende soorten pythagons mogen onderling maar 1 verschillen. (Dus je gebruikt bijvoorbeeld vijf pythagons 87 keer en twee pythagons 88 keer.)
- Schrijf op de mooiste manier het getal 2017, met 217 of meer pythagons. Je mag best het ene pythagon meer gebruiken dan het andere.
Vraag 1
Alle inzenders constateren dat de figuur die ontstaat zoveel mogelijk cirkelvormig moet zijn. Eén pythagon heeft oppervlakte 2. Dus 217 pythagons hebben oppervlakte 434. De oppervlakte van een cirkel is gelijk aan $πr^2$ en de omtrek is 2πr. In ons geval geldt r = √(434/π) ≈ 11,75, dus de omtrek is ongeveer 73,85. Uiteraard is deze grens onbereikbaar.
Er waren vier serieuze inzenders voor deze opdracht. Aad van de Wetering vond een figuur met omtrek 36 + 30√2 ≈ 78,43. Sandra van Wijk vond een figuur met omtrek 30 + 34√2 ≈ 78,08. Edo Timmermans vond een figuur met omtrek 54 + 20√2 ≈ 82,28. Op de valreep ontvingen we nog een inzending van Helmut Postl. Zijn inzending heeft een omtrek van 34 + 30√2 ≈ 76,43 (zie figuur 1). Daarmee heeft hij de kleinste omtrek gerealiseerd.
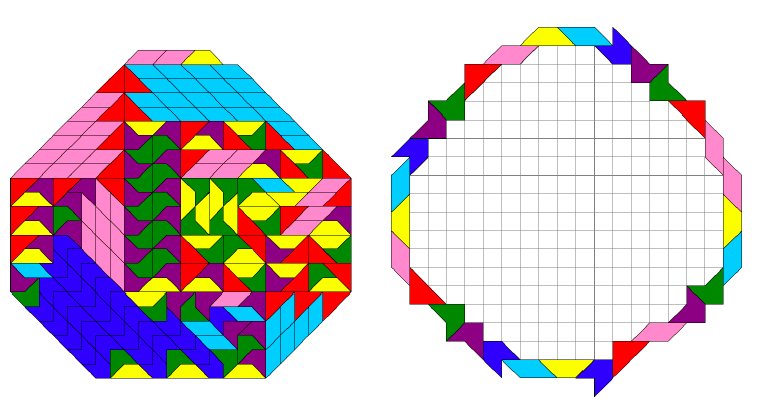
Figuur 2: OPlossing van vraag 2 door Helmut Post (rechts)
Vraag 2
Deze vraag was kennelijk lastig, want we kregen maar weinig inzendingen. Zowel Aad van de Wetering als Edo Timmermans konden het doen met 30 pythagons, terwijl Sandra van Wijk er 35 nodig had. Opnieuw had Helmut Postl de beste oplossing: hij had niet meer dan 29 pythagons nodig (zie figuur 2).
Vraag 3
De jury was onder de indruk van de leuke inzendingen; enkele ervan zie je in de figuren 3 tot en met 6 (op deze en de volgende pagina). We kregen veel foto’s, ook van zeer jeugdige lezers (vanaf 7 jaar), cijferontwerpen van schoolklassen, en er was een klas die een filmpje instuurde waarin 1 + (2 + 3 + 4 + 5) × 6 × (7 + 8 + 9) met pythagons wordt gemaakt (reken zelf de uitkomst maar uit). Het filmpje is te zien op onze Facebook-site.



Prijzen
Alle inzenders ontvangen enkele van onze fraaie getallenposters. Bovendien ontvangen Aad van de Wetering, Sandra van Wijk en Helmut Postl elk een cadeaubon van 20 euro. Aad en Sandra omdat zij elk een heel essay met hun bevindingen opstuurden, Helmut vanwege zijn optimale oplossingen. Tot slot krijgt ook klas 1Mod1 van KSO Glorieux in Ronse in België een cadeaubon, voor het filmpje dat deze leerlingen onder leiding van hun docent Lucrèce Vanheddegem hebben gemaakt.
