Opgave 437 ^[oOO]

Als je de laatste cijfers van de kwadraten van $1$ tot en met $2020$ bij elkaar optelt, wat is dan de uitkomst? 

Opgave 438 ^[oOO]

Neem drie gehele getallen $a, b, c$ met als gemiddelde het gehele getal $n$. Laat nu $p, q, r$ drie reële getallen zijn (niet van de vorm een geheel getal plus $\frac{1}{2}$), die eerlijk afgerond $a, b, c$ zijn. Bewijs dat het gemiddelde van $p, q, r$ afgerond ook $n$ is. 

Opgave 439 ^[ooO]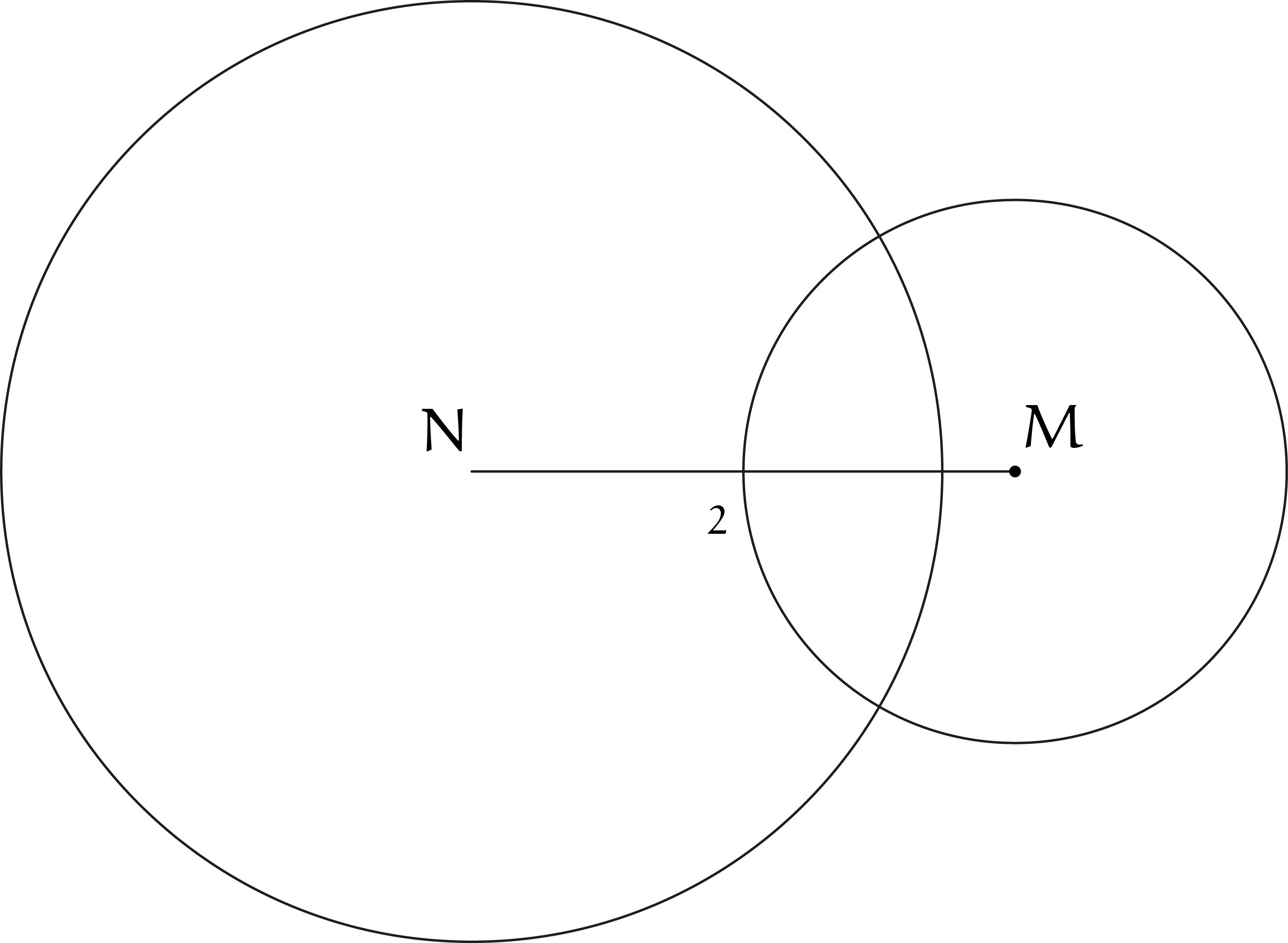

Gegeven zijn een cirkel met middelpunt $M$ en oppervlakte $\pi$, en een cirkel met middelpunt $N$ en oppervlakte $3\pi$. Gegeven is dat $|MN| = 2$. Bepaal de oppervlakte van het overlappende gebied van de twee cirkels. 

Opgave 440 ^[ooO]

Zij $n \ge 2$ een geheel getal. We kleuren de hoekpunten van een regelmatige $2n$-hoek rood of blauw. Hierbij moeten twee punten die precies tegenover elkaar liggen verschillende kleur hebben. We willen dat de resulterende kleuring rotatiesymmetrisch is. Voor welke waarden van $n$ is het mogelijk om de hoekpunten zo te kleuren?

Opmerking

Een kleuring is rotatiesymmetrisch als deze na draaien over een bepaalde hoek (kleiner dan $360^{\rm o}$) weer hetzelfde is. Het is voldoende om de juiste waarden van n te vinden en een kleuring te geven voor deze waarden van $n$. Een extra uitdaging is bewijzen dat het niet mogelijk is voor andere waarden van $n$.

Bekijk oplossing