Je inzending moet bij ons binnen zijn vóór

1 juli 2021

Opgave 449 ^[oOO]

Bewijs dat in iedere convexe vierhoek $ABCD$ geld dat

$$|AB| + |BC| + |CD| + |DA| > |AC| + |BD|.$$

(Een convexe vierhoek is een vierhoek zonder 'deuken'.)

Opgave 450 ^[oOO]

Er zitten 10 basisschoolkinderen van 4 t/m 12 jaar oud bij elkaar in een klaslokaal. Het blijkt dat wanneer er één willekeurig kind wordt weggestuurd, de gemiddelde leeftijd van de overgebleven kinderen altijd een geheel getal is.

Bewijs dat de gemiddelde leeftijd van alle kinderen een geheel getal is. Klopt deze conclusie ook als ze van 4 t/m 13 jaar kunnen zijn?

Opgave 451 ^[ooO]

Laat $a$ en $b$ twee getallen zijn van twee cijfers, beide niet beginnend met een $0$. Stel dat $a^2 + b^2$ gelijk is aan het getal dat we krijgen als we $a$ en $b$ achter elkaar schrijven.

Wat zijn alle mogelijke tweetallen $a$ en $b$ met deze eigenschap?

Opgave 452 ^[ooO]

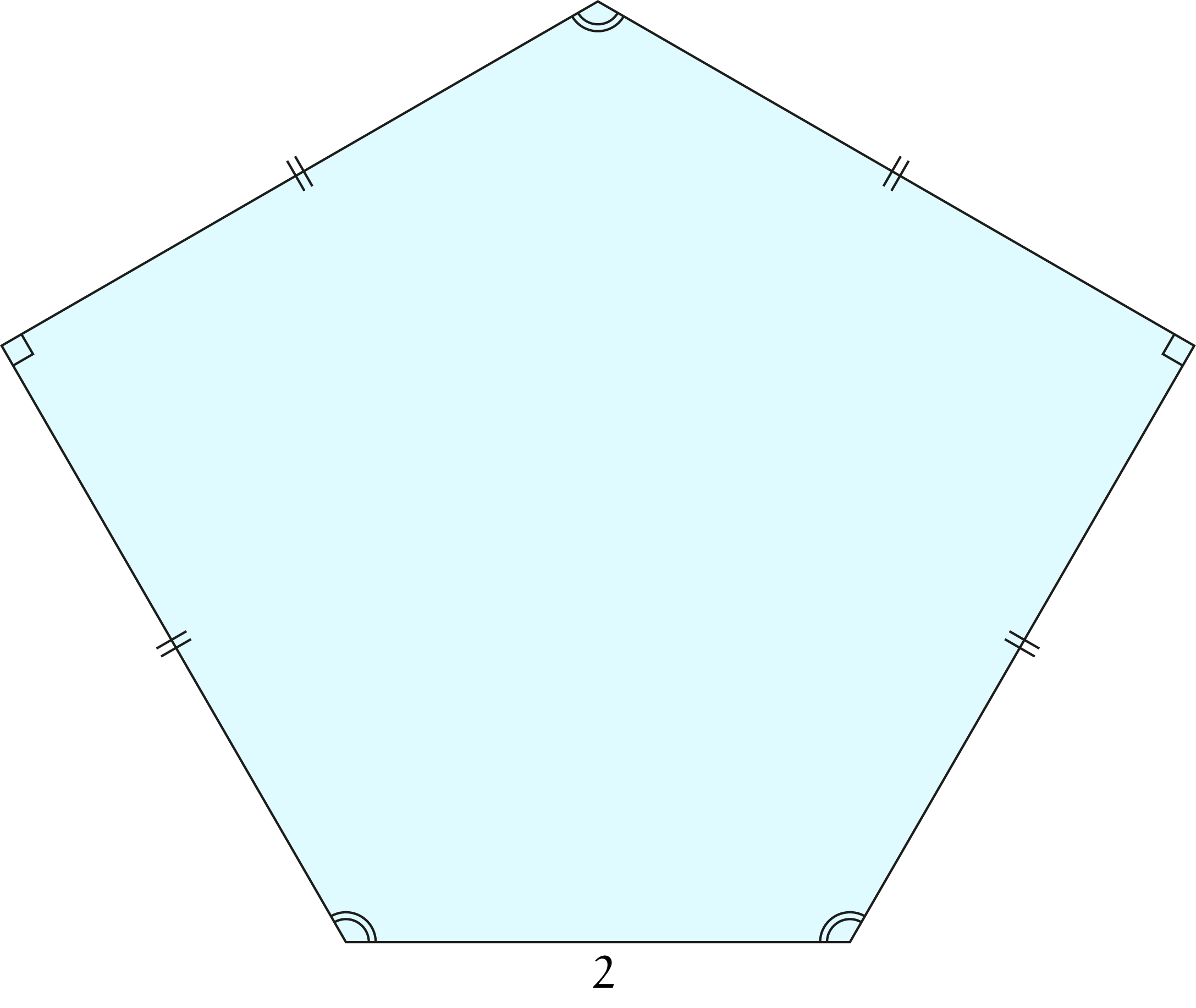
Hieronder is een vijfhoek weergegeven met twee rechte hoeken. De overige drie hoeken zijn gelijk. De zijde aan de onderzijde heeft lengte $2$ en de andere vier zijdes zijn allemaal even lang.

Bepaal de lengte van deze overige zijden (zie ook het artikel over de prijsvraag).