Opgave 457 [oOO]

Bas geeft een volledig verantwoord feestje, waarvoor hij vijf gasten heeft uitgenodigd. Hij bestelde voor de gelegenheid vijf pizza's, maar bedenkt zich nu plots dat hij zelf eigenlijk ook wel wat pizza lust. Hij besluit de pizza's te verdelen over alle zes de aanwezigen zodat iedereen evenveel krijgt. Bas kan de cirkelvormige pizza's enkel volledig doorsnijden over een rechte lijn van korst naar korst, die door het middelpunt van de pizza gaat. Hoeveel van zulke doorsnijdingen moet Bas minimaal maken om de pizza's eerlijk te kunnen verdelen?

Opgave 458 [oOO]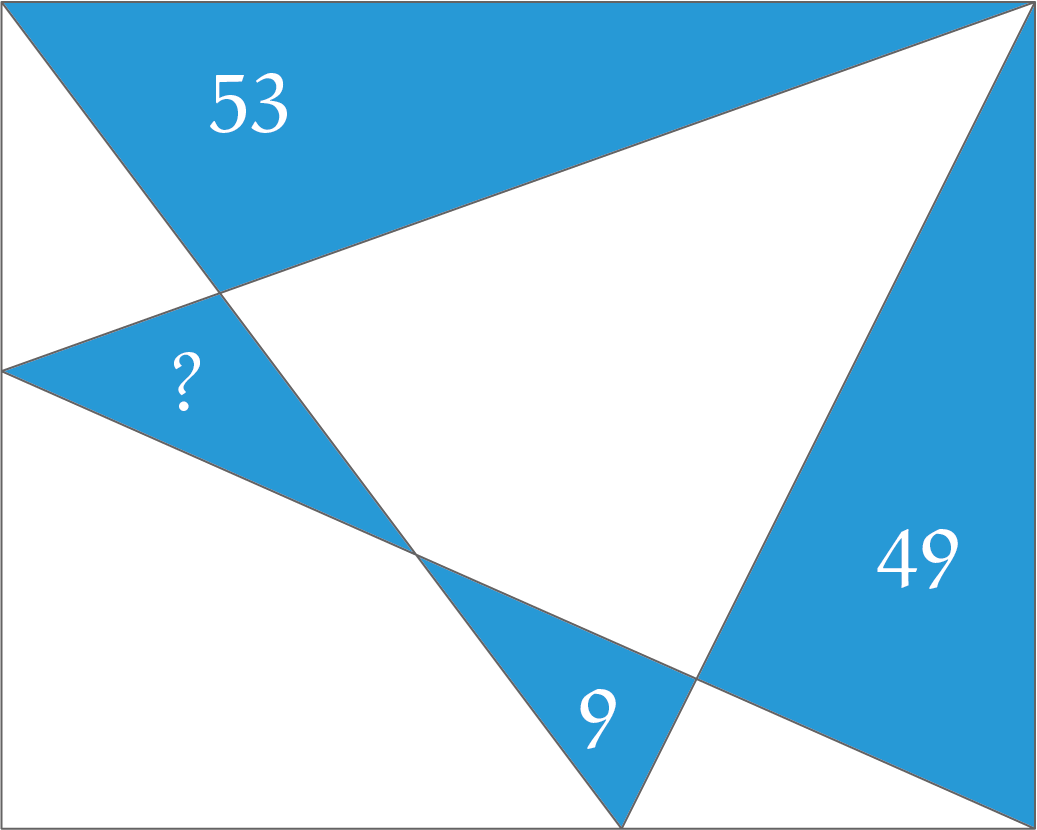

In de rechthoek in de figuur hiernaast zijn vier lijnstukken getekend. Van een aantal gebieden is de oppervlakte aangegeven. Wat is de oppervlakte van het gebied met het vraagteken?

 

Opgave 459 [ooO]

Felix heeft $25$ gewichtjes die allemaal bijna hetzelfde gewicht hebben, maar in werkelijkheid allemaal verschillend zijn. Hij zou graag de drie zwaarste gewichtjes uitzoeken, maar hij kan zelf het verschil niet voelen. Gelukkig heeft hij een heel precieze sorteermachine voor gewichtjes, waarin hij vijf gewichtjes kan plaatsen die de machine vervolgens sorteert in oplopende volgorde van hun gewicht. Het gebruiken van de sorteermachine is echter heel duur, dus Felix zou deze het liefst zo weinig mogelijk gebruiken. Wat is het minimale aantal keer dat hij de machine moet gebruiken
om de drie zwaarste gewichtjes te vinden?

Opgave 460 [ooO]

We bekijken een gelijkbenige rechthoekige driehoek waarvan de rechthoekszijden lengte $1$ hebben. Drie cirkels raken aan de zijden van de driehoek en aan elkaar zoals in de figuur hieronder. 

Wat is de straal van de kleinste cirkel?

Bekijk oplossing