Pythagoras Olympiade 61-3, januari 2022
Inzenden kan alleen per e-mail. Stuur je oplossing (getypt of een scan of foto van een handgeschreven oplossing) naar [email protected]. Je ontvangt een automatisch antwoord zodra we je bericht hebben ontvangen.
Voorzie het antwoord van een duidelijke toelichting (dat wil zeggen: een berekening of een bewijs). Vermeld je naam en adres; leerlingen moeten ook hun klas en de naam van hun school vermelden.
Je inzending moet bij ons binnen zijn vóór 10 februari 2022.
Opgave 465 [oOO]
Het getal $26$ heeft de eigenschap dat als we een rekenkundige rij met haar cijfers maken, we na een aantal stappen weer op $26$ uitkomen; namelijk middels $2 - 6 - 10 - 14 - 18 - 22 - 26$. Hoeveel getallen van $2$ cijfers hebben deze eigenschap?
 Opgave 466 [oOO]
Opgave 466 [oOO]
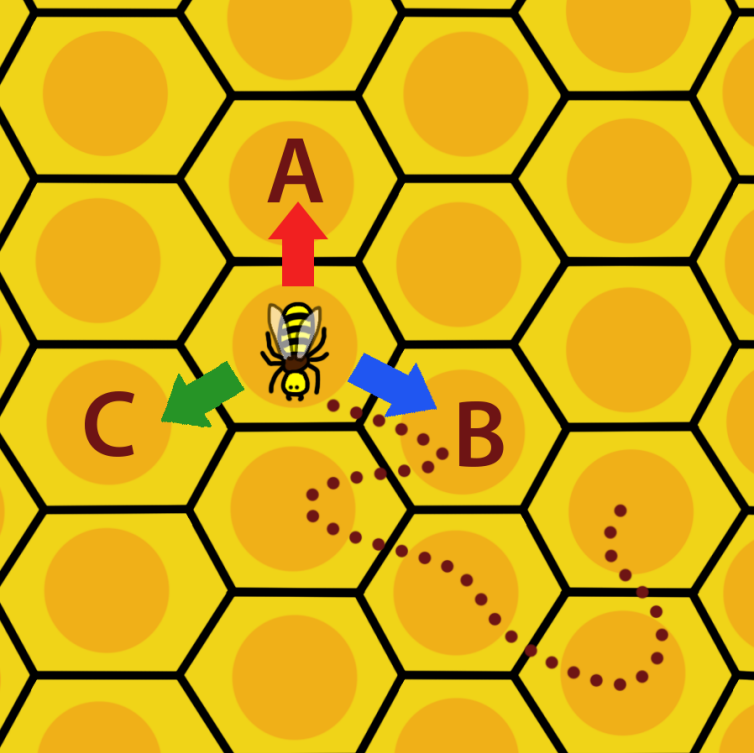
Een bij loopt op een honingraat aan de hand van de instructies van z'n koningin. Als hij A hoort, dan loopt hij één cel naar boven. Bij B loopt hij een cel naar rechtsonder en bij C een cel naar linksonder, zie de afbeelding. Hier is ook het pad aangegeven dat hij aflegt als hij achtereenvolgens BCBBA te horen krijgt. Nu geeft de koningin nooit de afzonderlijke lettercombinaties door als instructies, maar in plaats daarvan alleen combinaties bestaande uit de stukjes ABA, BCBC en CCA.
Welke cellen kan de bij met één of meer van deze commando's bereiken?
Opgave 467 [ooO]
Laat $x$ en $y$ twee breuken zijn. Stel dat $x^2 + y$ en $x + y^2$ allebei gehele getallen zijn.
Bewijs dat $x$ en $y$ zelf ook al geheel waren.
Geldt die conclusie nog steeds wanneer enkel bekend is dat $x$ en $y$ twee reële getallen zijn met diezelfde eigenschap?
Opgave 468 [ooO]
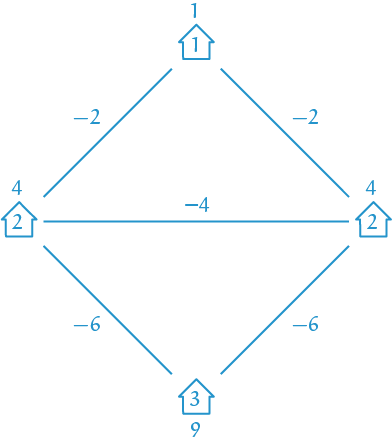
Een zeker koninkrijk bestaat uit vier steden en vijf wegen, zie de afbeelding. De steden komen in verschillende types. Type 1 is het kleinst, type 2 is groter, type 3 is nog groter, enzovoorts. Een stad van type $n$ levert precies $n^2$ goudstukken per maand op aan belasting. Een weg tussen een stad van type $n$ en een stad van type $m$ kost echter $nm$ goudstukken per maand aan onderhoud. In het voorbeeld zie je een voorbeeld van een land waarin de koning elke maand twee goudstukken verlies maakt. Vind oneindig veel verschillende verdelingen van stadtypes zodat de koning precies $1$ goudstuk per maand aan winst heeft.
Bonus: toon aan dat het niet mogelijk is dat de koning precies $2$ goudstukken per maand aan winst overhoudt.