Inzenden Je inzending moet bij ons binnen zijn vóór 10 juli 2022

Opgave 473 ^[oOO]

We schrijven de getallen $1$ tot en met $2022$ achter elkaar op het bord. Hoeveel vaker schrijven we het cijfer $1$ op dan het cijfer $9$?

Opgave 474 ^[oOO]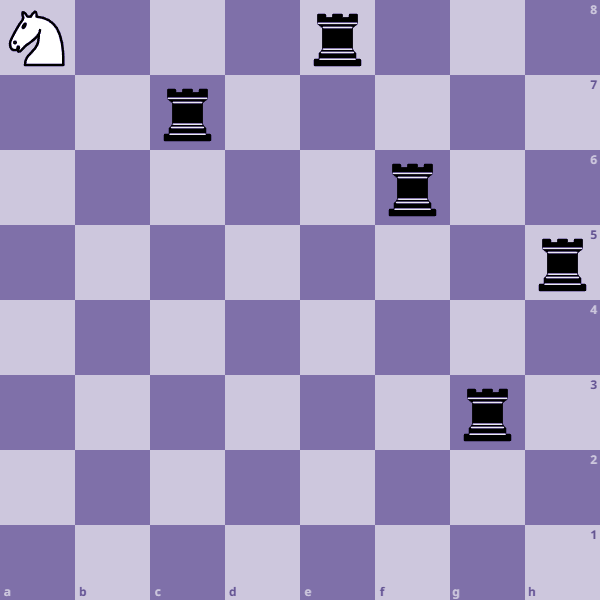

Een wit paard staat op een hoekvakje van een schaakbord. We willen zwarte torens neerzetten op zo'n manier dat geen van de torens elkaar kunnen zien (dat wil zeggen, in dezelfde rij of dezelfde kolom staan) en tevens zodat het paard elke zet een toren kan slaan (de torens bewegen zelf niet) tot alle torens geslagen zijn. In het voorbeeld vind je zo'n configuratie met vijf torens. Hoeveel torens kunnen we maximaal plaatsen?

Opgave 475 ^[ooO]

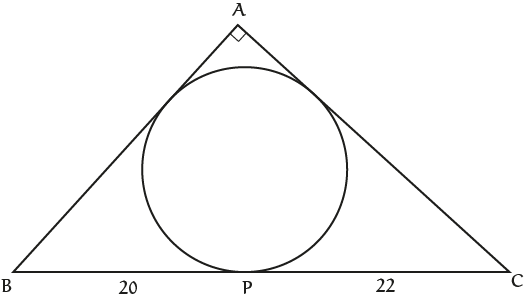
Zij $ABC$ een driehoek met $\angle A = 90^{\rm o}$. Laat $P$ het raakpunt van de ingeschreven cirkel met zijde $BC$ zijn. Stel dat $|BP| = 20$ en $|CP| = 22$. 

Bepaal de oppervlakte van driehoek $ABC$.

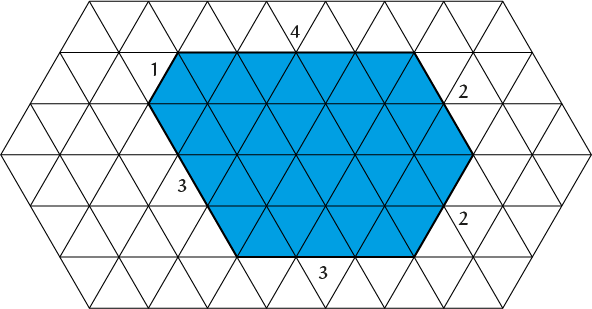
Opgave 476 ^[ooO]

We tekenen in een driehoekig rooster een zeshoek met zijden $a$, $b$, $c$, $d$, $e$ en $f$. In het voorbeeld vind je een tekening van een zeshoek
met $(a, b, c, d, e, f) = (3, 3, 1, 4, 2, 2)$ en je kunt nagaan dat deze zeshoek uit precies $35$ kleine driehoekjes bestaat. Vind een formule voor het aantal driehoekjes in de zeshoek in termen van $a$, $b$, $c$, $d$, $e$ en $f$.

Bekijk oplossing