Inzenden kon tot 1 augustus 2024

Opgave 521 ^[oOO]

Drie klasgenoten hebben ruzie, maar hebben alle drie een kaartje gekocht voor dezelfde film. Tot overmaat van ramp moeten ze zelfs zitten in dezelfde rij van 10 stoelen die naast elkaar staan.

Op hoeveel manieren kunnen ze plaatsnemen zonder dat twee klasgenoten direct naast elkaar hoeven te zitten?

Opgave 522 ^[oOO]

Anouk en Marleen wonen samen in een studentenhuis, en vinden het heel gezellig om samen een weekend door te brengen. Helaas lopen ze elkaar nogal vaak mis. Driekwart van de weekenden dat Anouk thuis is, is Marleen er niet. En de helft van de weekenden dat Marleen thuis is, is Anouk er niet.

Welk deel van de weekenden brengen ze maximaal samen door?

Opgave 523 ^[ooO]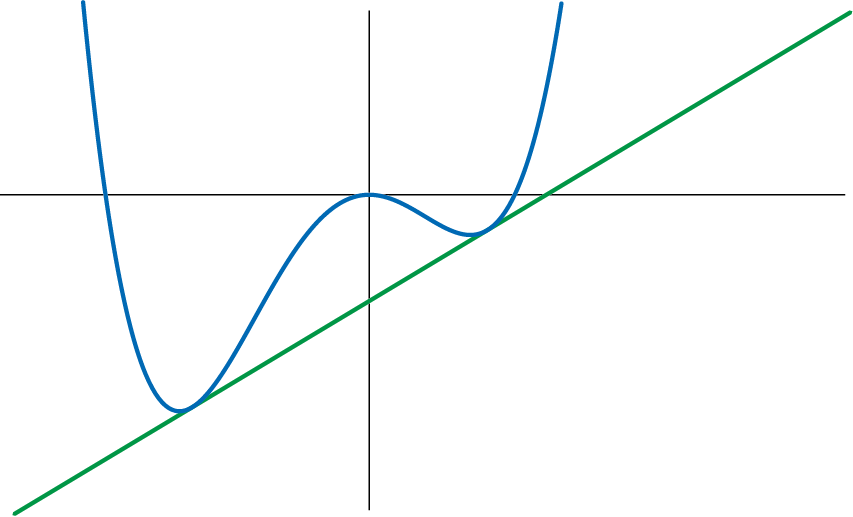

Beschouw de functie $f(x) = x^4 + 2x^3 - 11x^2$.

Er bestaat precies één lijn die de grafiek van $f$ in precies twee verschillende punten raakt.

Wat is de formule voor die lijn?

Opgave 524 ^[ooO]

Op de online spellensite Sterrenrijk heeft iedere speler een rang, die aangeduid wordt met een natuurlijk getal. Als je je voor het eerst aanmeldt krijg je rang $1$. Je kan dan online tegen een andere speler een spelletje doen. Spelletjes hebben altijd een winnaar, remise komt niet voor. Als je begint met rang $n$, dan heb je een score van $0$. Win je een spelletje, dan krijg je een punt erbij. Verlies je een spelletje, dan gaat er een punt van je score af, maar je score kan nooit onder de $0$ zakken. Zodra je een score van $n$ punten hebt, ga je door naar rang $n + 1$, en wordt je score weer op $0$ gezet. Bijvoorbeeld: als je rang $1$ hebt en een spelletje wint, ga je naar rang $2$. Als je daarna een spelletje verliest en dan twee spelletjes wint, ga je naar rang $3$. Als je daarna twee spelletjes wint, een verliest en dan een wint, sta je op $2$ punten maar mag je nog niet naar rang $4$. Je kan nooit terugzakken onder je huidige rang.

Veronderstel dat je ieder spelletje met een kans van $50\%$ wint of verliest. Hoeveel spelletjes zou je er naar verwachting over doen om van rang $n$ naar rang $n + 1$ te komen? En wat als je een kans van $1/3$ hebt om te winnen? Of $2/3$?

Bekijk oplossing