Inzenden vóór 15 juli 2025

Opgave 545 ^[oOO]

Niet iedereen kan een kwadraatjaardag vieren: dat is het vieren van je $n$de verjaardag in het jaar $n^2$. We noemen de mensen met hun kwadraatjaardag in het jaar $n^2$ als behorende tot generatie $n$. Als we ervan uitgaan dat mensen hoogstens $90$ jaar oud worden, in welk jaar vieren de mensen van de laatste generatie $n$ die nog mensen uit generatie $n + 1$ kunnen ontmoeten hun kwadraatjaardag?

Opgave 546 ^[oOO]

We bekijken getallen van de vorm $100\dots 001$. Voor welke aantallen nullen is dit getal deelbaar door $11$?

Opgave 547 ^[ooO]

Er geldt $(20 + 25)^2 = 2025$. Er bestaan nog twee jaartallen $ABCD$ van vier cijfers die voldoen aan de vergelijking

$(AB + CD)^2 = ABCD$.

Welke jaartallen hebben deze heel bijzondere eigenschap?

Opgave 548 ^[ooO]

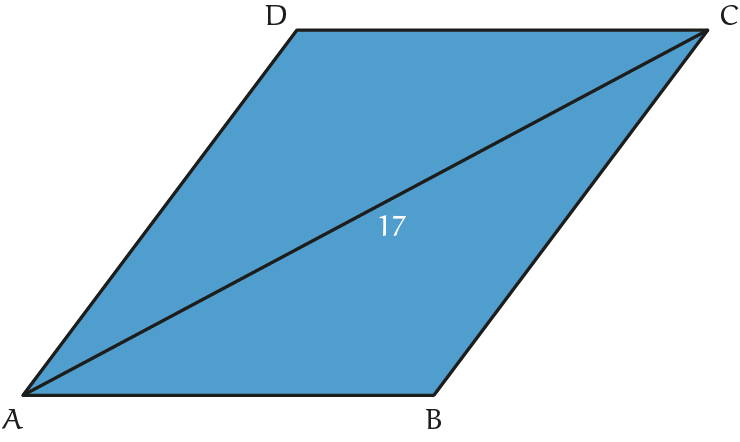
Zij gegeven een parallellogram $ABCD$ met oppervlakte $72$, omtrek $38$ en lange diagonaal $17$. Bepaal de lengte van de andere diagonaal.

 

Je inzending moet bij ons binnen zijn vóór 15 juli 2025 via [email protected].