Beide wandelingen zijn geweldig. Er is een groot verschil in aanpak: in Leuven heeft men met een groot team van docenten en leerlingen een werkelijk perfecte wandeling neergezet, in Veenendaal is de hele wandeling het werk van één leerling. Beide inzendingen verdienen een abonnement op Pythagoras. De inzending uit Veenendaal heeft (nog?) geen bijbehorend filmpje, maar dat kan in de toekomst nog gemaakt worden.

Het filmje uit Leuven is te zien YouTube. We gaan dit jaar met de wedstrijd door, omdat we graag het hele gebied waar Pythagoras wordt gelezen met wiskundewandeltochten willen overdekken.

De wandeling in Veenendaal

De wandeling in Veenendaal is dermate aantrekkelijk dat ik met de trein naar Veenendaal ben gegaan om hem te lopen. De wiskundewandeling vanaf het Christelijk Lyceum in Veenendaal (52,013139 N, 5,45111 O), de coördinaten van het schoolgebouw krijgen we er meteen bij, gaat langs moderne meetkundige objecten in de buurt. Er wordt aangekondigd dat de wandeling veel langer dan 90 minuten duurt en dat de opgaven waar een vlammetje of een klokje voor staat beter eerst kunnen worden overgeslagen. In figuur 1 zie je de vijf gehanteerde moeilijkheidsgraden.

De afstanden in de wandeling worden gegeven in stoeptegels, zodat de wandelaar meteen aan het schatten slaat. De geografische coördinaten doen je verwachten dat daar een vraag over komt. Dit is een kans voor de toekomst.

Moeilijke vragen

De eerste paar vragen zijn behoorlijk moeilijk. Voor de school staat een kubus met aan alle vier de kanten een voorstelling. De opgave gaat over twee kanten van het mozaïek, met rode, gele, witte en blauwe tegels op een grijze achtergrond (zie figuur 2). De letters $B, W, G$ en $R$ stellen de kleuren blauw, wit, grijs en rood voor. Er worden vijf betrekkingen gegeven over de oppervlaktes van de kleuren, zoals $G \le 8(B + W).$ Je moet er twee weg nemen zodat het overblijvende stelsel van drie betrekkingen klopt.

Dit is wiskundig een heel leuke opgave. De volgende opgave gaat over het logo van de school. Ook daar worden vergelijkingen gegeven over de oppervlakte. Het kan voor de wandelaar ook heel spannend zijn om die vergelijkingen zelf op te stellen, aan de hand van wat je ziet. Bij de mozaïekvraag zou je ook best de wandelaar kunnen vragen om de blauwe, witte, grijze en rode oppervlakten te ordenen naar grootte. Bij het logo van de school is het heel leuk om de verhouding tussen het gele en het blauwe deel te schatten (figuur 3).

De opgave met de K

Intrigerend, aantrekkelijk, maar moeilijk is de opgave over het logo van het bedrijf Kubiek (figuur 4). Het logo bestaat uit een groot vierkant met zijden van lengte 1. Het vierkant is verdeeld in vier veelhoeken, door drie lijnen waarvan twee loodrecht op de zijkant van het vierkant en een met een hoek van 45°. Alle vier de veelhoeken hebben dezelfde omtrek.

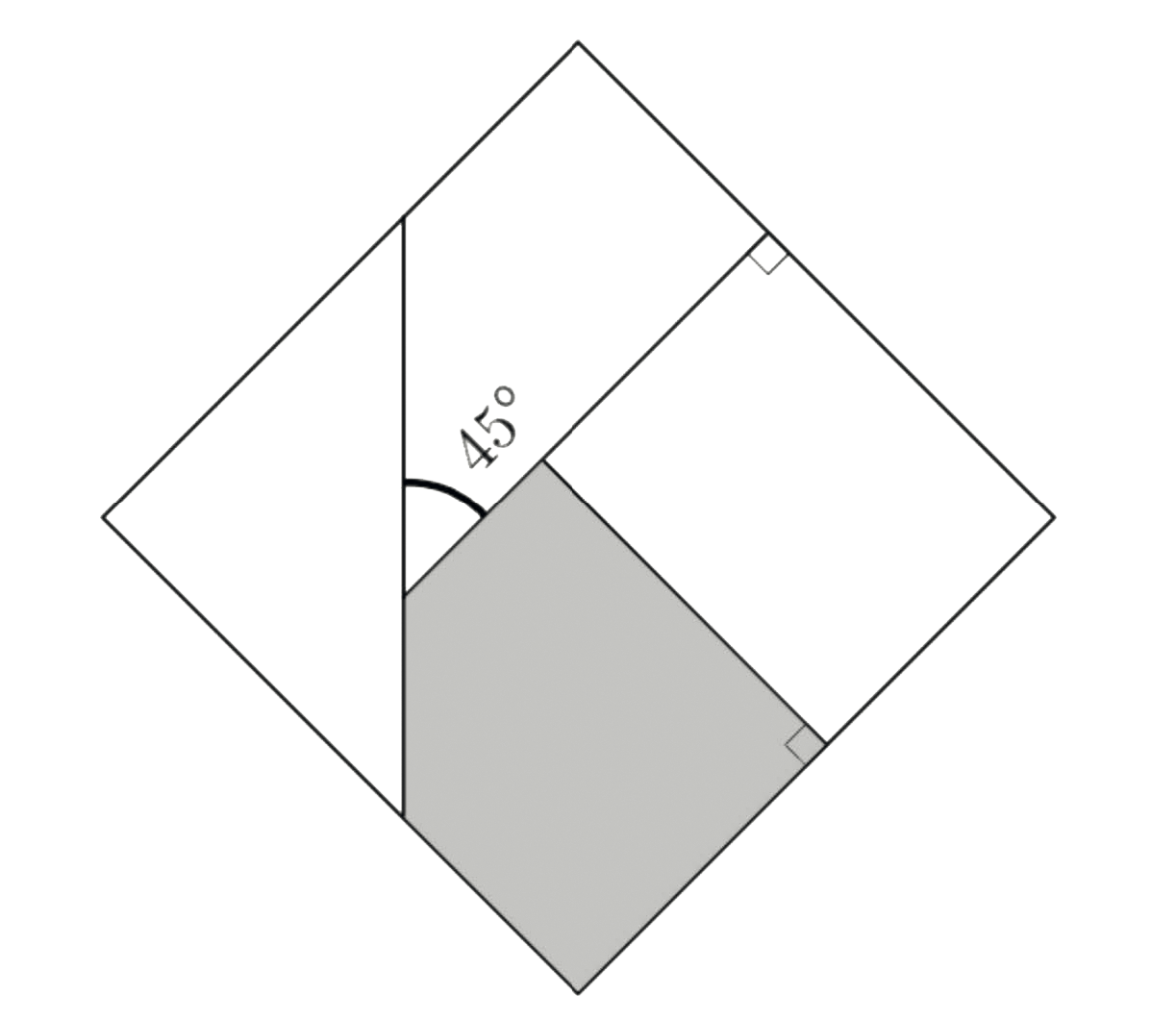
Hoe groot is de oppervlakte van de grijze veelhoek in figuur 5? Na een flinke rekenpartij met drie vergelijkingen met drie onbekenden kom ik tot het antwoord:

$$\frac{3}{529}\left(7+17\sqrt{2}\right)\approx 0{,}293$$

Wat zou je nog meer kunnen doen met dit prachtige logo?

Wat is een goede vraag?

De vraag uit de wandeling in Veenendaal over een in een vierkant geplaatste letter K is intrigerend. Het object is zeer geschikt, alleen: wat voor vragen zijn er mogelijk?

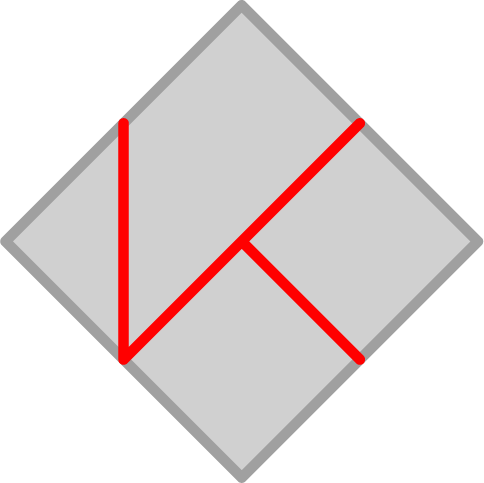
Het valt tegen dat er zo’n grote berekening aan te pas komt en het uiteindelijke antwoord is gecompliceerd.

Het proberen van andere varianten, bijvoorbeeld waarbij de oppervlaktes in een bepaalde verhouding moeten staan of waarbij de hoekpunten van de letter K de hoeken van een vierkant moeten vormen, levert niet zomaar succes. Het laatste probleem is weer te simpel, en dit levert een K in figuur 6 op die niet erg meer lijkt op het voorbeeld van het logo.

Hoe maak je een goede vraag? Uit de chaos van de probeersels (het creatieve proces) hoop je te komen tot iets eenvoudigs en verrassends. Een schema dat kan helpen bij het komen tot goede opgaven voor een wiskundewandeling staat hieronder. Let wel: dit is natuurlijk ook gebaseerd op persoonlijke voorkeuren.

1. Vind iets in je omgeving waar je wiskundig iets interessants aan kan opmerken. Je hoeft er nog geen vraag bij te hebben. Bijvoorbeeld een scheve boom, een grid in een metalen hek, een golvende muur in een gebouw, een bloem met symmetrische blaadjes enz.

2. Overdenk wat je wiskundig interessant vindt aan het object. Wat zou je willen weten over het object?

3. Vereenvoudig, idealiseer de situatie.

4. Maak je berekeningen. Als deze te ingewikkeld of te lelijk worden (weer: persoonlijke voorkeur) ga verder met vereenvoudigen of zelfs met het veranderen van het probleem. Als het te eenvoudig wordt of te saai, introduceer weer meer details. Ga hier net zo lang mee door totdat je er tevreden over bent. (Aandachtspunten: (1) Is het uitgangspunt eenvoudig genoeg voor de op te lossen vraag? (2) Is de uitkomst mooi genoeg? (3) Zijn er precies genoeg gegevens om het op te lossen? (4) Wordt het leuker als je andere aspecten van je onderwerp als gegevens gebruikt? Of als je bij het antwoord begint als uitgangspunt?)

5. Als je tevreden bent: heb je het probleem zo eenvoudig mogelijk en ondubbelzinnig geformuleerd? Probeer je vraagstuk uit op je wiskundige omgeving en herhaal zonodig dit proces.

Mijn versie van de letteropgave, die ook al in het vorige nummer stond, is als volgt. Het ontstond na een groot aantal te moeilijke en enkele te saaie problemen. Ik zeg niet dat dit beter is, dat is persoonlijk. (Ik heb namelijk wel veel plezier beleefd aan de originele opgave over de K.)

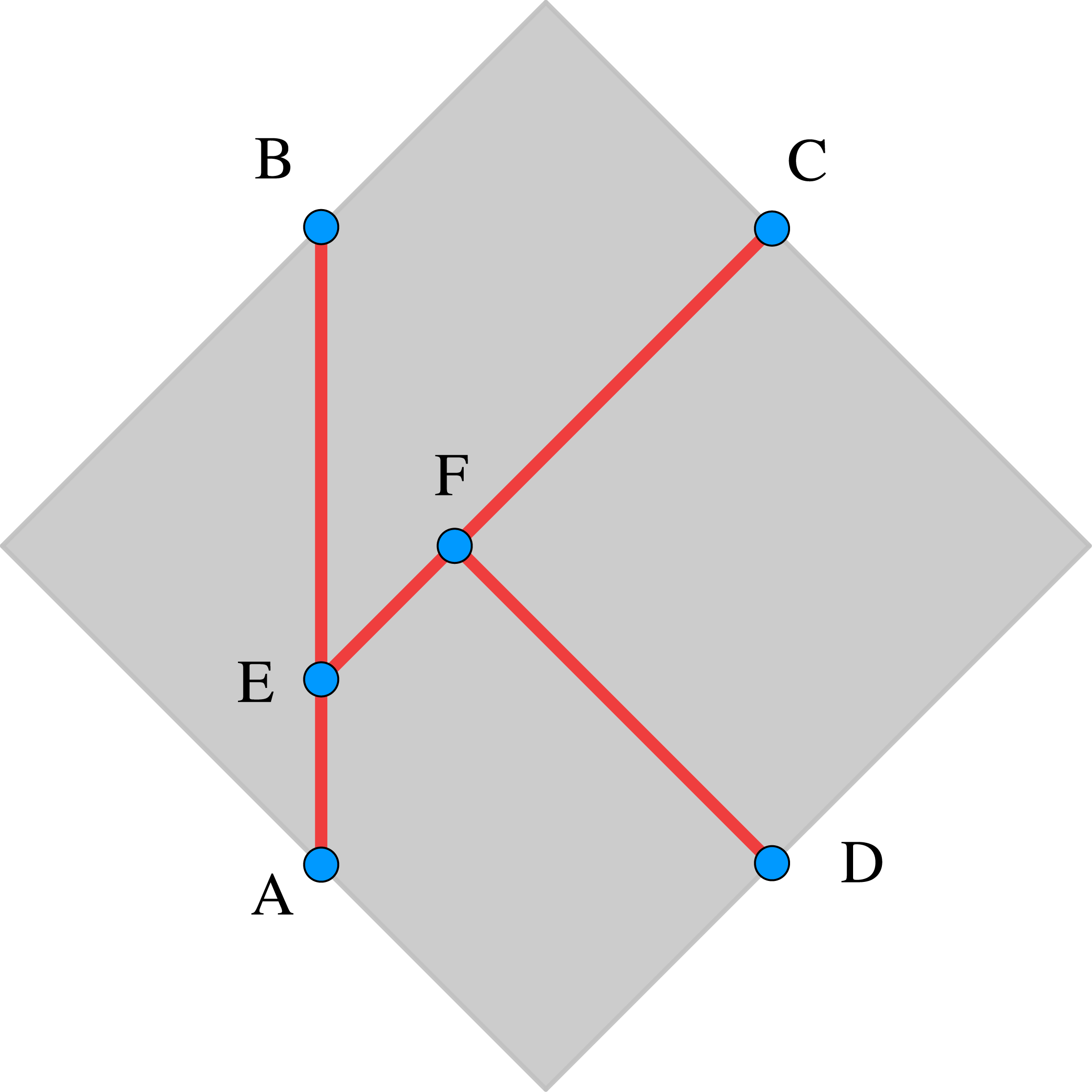Opgave

In nevenstaand gekanteld vierkant met zijde 1 staat de letter K getekend. Lijnstuk $AB$ maakt een hoek van $45^{\rm o}$ met de zijkant, $\angle BEF = 45^{\rm o}$ en $\angle EFD = 90^{\rm o}$. De zijden $AB$ en $CE$ zijn even lang en de punten $A, B, C$ en $D$ vormen een rechthoek.

Bereken $DF.$

Humor

Er is een vraag over een rijschema van een bus, waarbij aan ons wordt gevraagd om ‘begrijpend te kijken’. Een bepaald huisnummer is een zuiver imaginair getal: 115i. Daar komt ook een leuke opgave bij.

Nog een humoristische opgave luidt: “Op een zeker moment, lang geleden, was de prijs van diesel 106,9 cent per liter. Nu is de prijs hoger. Bereken de toename in centen, gedeeld door de procentuele toename.”

De wandeling eindigt bij het gemeentehuis, waar een vraag komt over de meetkundige structuur van de plafondverlichting. Het is verbazend dat in het dorp Veenendaal zoveel, vooral meetkundig interessante objecten te zien zijn. Het is een verdienste van Casper de With dat hij deze allemaal voor ons heeft opgezocht en er leuke opgaven bij heeft bedacht.

De wandeling in Leuven

De wandeling in Leuven is een prachtig uitgevoerd boekje van 24 bladzijden. Er zijn drie verschillende niveaus en de geschiedenis speelt bijna overal een belangrijke rol. Dat kan ook haast niet anders met zo’n stad. Het maken van de wandeling is ook een goed idee als je de stad cultureel wilt leren kennen. Er wordt veel aandacht besteed aan het geven van algemene informatie over elke interessante plaats.

De wandeling begint in het stationsgebouw van Leuven. De koepels waar de overkapping uit bestaat moeten worden gefit in een parabool. De schatting moet de lezer zelf doen en daarna kan hij zijn antwoord geven door middel van een multiple choice.

Dorre de Bakkerszoon

Een erg leuk raadsel wordt ons opgegeven bij een standbeeld Dorre de Bakker in figuur 7. Deze Dorre is de zoon van de bakker en mag een uur op de bakkerij van zijn ouders passen.

Het raadsel gaat als volgt: op het uurtje dat Dorre in de bakkerij stond, kwamen er drie mannen langs om taarten te kopen en waren alle taarten op. Toen zijn ouders terugkwamen en aan Dorre vroegen hoeveel taarten hij verkocht had, wist hij het niet meer. Hij dacht terug aan wat de mannen besteld hadden. Hij wist niet meer hoeveel taarten ze allemaal hadden besteld, maar dit wist hij nog wel: hij had geen enkele taart doormidden moeten snijden, met andere woorden: elke persoon kocht een geheel aantal taarten. De eerste man kocht de helft van de taarten plus nog een halve taart. Van de overgebleven taarten kocht de tweede man weer de helft plus nog een halve taart. Van de taarten die toen nog overbleven kocht de derde man ook weer de helft plus een halve taart.

Hoeveel taarten heeft Dorre die dag verkocht?

(a) 15 (b) 9 (c) 7 (d) 11

De hemelglobe van KangXi-Verbiest

Een werkelijk schitterend object voor opgaven is de hemelglobe van KangXi-Verbiest in figuur 8. De schrijvers van de Leuvense wandeling maken er ook een mooie opdracht over.

Er wordt gevraagd een hoek te bepalen tussen de zon, de aarde en een ster van sterrenbeeld Schorpioen. Gegeven is dat de ecliptica samenvalt met de horizontale buitenring van de hemelglobe. Op de hemelglobe is vast te zien dat alle sterrenbeelden van de dierenriem, en dus ook Schorpioen op de ecliptica liggen. Op de hemelglobe wordt een hoek geteld in drakenhoofden die op een grootcirkel om de hemelglobe heen te vinden zijn. Er wordt gegeven dat het 180 drakenhoofden zijn. Met zo’n vraag gebruik je echt dat de wandelaar het object waar je iets over vraagt kan zien en kan bestuderen. Erg mooi!

Het museum M

Meetkundig intrigerend is ook de trap van het kunstmuseum M. De trap van dit museum bestaat enerzijds uit treden, maar is ook een zeer geleidelijk stijgend pad. Het is prachtig dat de Leuvense wandeling je ook langs dit mooie gebouw voert.

De Leuvense wandeling associeert er vrij op los: soms hebben de wiskundige problemen niets te maken met het object waaraan de vraag gekoppeld is, zoals bij de gevangenis. Ook maakt de multiple choice benadering soms dat de puzzelaar minder diep hoeft na te denken om toch tot het goede antwoord te komen. De multiple choice benadering maakt de wandeling wel geschikt om als wedstrijd te gebruiken. De wandeling is heel goed afgestemd op precies het niveau van drie soorten deelnemers. Je kan hem als slimme tienjarige prima lopen.

De Leuvense wandeling is een prachtig afgewerkt geheel en mooi uitgevoerd. Ik moet dus binnenkort ook naar Leuven!

Prijzen

Beide bijdragen krijgen van ons een eerste prijs. Casper de With voor zijn scherpe observatievermogen, creativiteit en ook ironie, en het Leuvense team voor het geheel en het hoge niveau van afwerking. We gaan met veel energie voort met de wedstrijd: we hopen dat er na een paar jaar vele honderden wandelingen zullen zijn, verspreid over Nederland en Vlaanderen.

En ook als je uit Veenendaal of Leuven komt en je ondanks deze uitmuntende inzendingen wilt meedoen met je klas: er zijn altijd weer nieuwe dingen te verzinnen, in de buurt van je school, of zomaar naast de weg. Ook kan je thema’s verder uitwerken waar bovenstaande deelnemers aan zijn begonnen. Zou er een wiskundewandeling bestaan die helemaal gebaseerd is op lengte- en breedtegraden?