Sommige rijen voldoen aan een speciale eigenschap, namelijk dat er een zogenaamde recurrente (of recursieve) relatie bestaat, dat wil zeggen dat er een recept bestaat waarbij het volgende getal in de rij kan worden uitgerekend uit een aantal (meestal 1 of 2) vorige getallen uit die rij. Een heel bekend en historisch voorbeeld is de rij van Fibonacci:

$$0, 1, 1, 2, 3, 5, 8, \dots$$

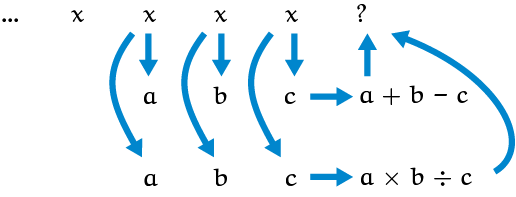
waarbij er een relatie bestaan tussen het volgende getal in de rij en de twee vorige (zie je welke relatie dat is?). Zo’n recurrentie stelt je in staat om uitgaande van een paar getallen in het begin van de rij, de hele rij te berekenen. In principe althans, want uiteraard kan dat een hoop tijd kosten. We kijken nu naar een andere rij. Dat is een rij waarin je het volgende getal kunt berekenen als je de vorige DRIE getallen weet. Het recept is: neem de vorige drie getallen, neem de som van de eerste en de derde, en trek daar het middelste getal van af. Dan krijg je het volgende getal in de rij.

Bijvoorbeeld, als we starten met:

$1, 2, 5$
	$1 + 5 - 2 = 4$
$1, 2, 5, 4$
		$2 + 4 - 5 = 1$
$1, 2, 5, 4, 1$
			$5 + 1 - 4 = 2$
$1, 2, 5, 4, 1, 2$
				$4 + 2 - 1 = 5$
$1, 2, 5, 4, 1, 2, 5$
					$1 + 5 - 2 = 4$
$1, 2, 5, 4, 1, 2, 5, 4$

Wat valt op? We draaien in een cirkel rond. Hoe kan dit? Een simpele check leert dat we geen rekenfout hebben gemaakt. Zou het misschien komen door onze toevallige keuze van de eerste drie getallen? Probeer eens een ander begin. Je zult zien dat je nieuwe rij ook weer repeteert na elke vier getallen. Alsof er een geheugen zit in de constructie die het mogelijk maakt uit de staart de hele voorgeschiedenis te reconstrueren. Dat is wel intrigerend, niet? Je kunt de optel/aftrekregel vervangen door een vermenigvuldig/deel regel. Kijk maar. Begin met:

$2, 4, 6$
	$2 \times 6 \div 4 = 3$
$2, 4, 6, 3$
		$4 \times 3 \div 6 = 2$
$2, 4, 6, 3, 2$
			$6 \times 2 \div 3 = 4$
$2, 4, 6, 3, 2, 4$

enzovoorts.

En je ziet het al gebeuren: het rijtje van $4$ gaat zich ook weer herhalen. We kunnen zeggen dat de 'periode' van deze rij $4$ is.

 

Opgave Kun je inzien dat ons eerste recept (pak de laatste drie getallen tot dusver, tel eerste en laatste op, trek middelste af) of het tweede recept (vermenigvuldig eerste en laatste getal, en deel door de middelste) leidt tot een periode van $4$? Kun je inzien dat als het ene recept periode $4$ heeft, het andere recept dan ook periode $4$ heeft?

Zijn er ook recurrente recepten die rijtjes genereren met andere perioden dan $4$? Het gaat te ver om dat allemaal te berekenen hier, maar het antwoord is ja. Het is mogelijk om een recurrentie te maken op basis van de laatste twee getallen voor een getallenrij met periode $k$ in $N$, voor elke $k \ge 3$. Die recurrentie heeft de vorm zoals in de volgende figuur.

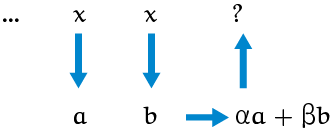
Hierbij zijn $a$ en $b$ (vaste) reële getallen. Kies $a = -1$ en $b = 2 \times \cos(2\pi/k)$.

Voorbeeld: $k = 4$: dan $a = -1$ en $b = 0$. Neem als start $a = 2$ en $b = 3$. Je krijgt:

Stap	$a$	$b$
$1$	$2$	$3$
$2$	$3$	$-2$
$3$	$-2$	$-3$
$4$	$-3$	$2$
$5$	$2$	$3$
$6$	$3$	$-2$ (enzovoort)

Je ziet: een perfecte periode $4$. Het resulterende rijtje is:

$2, 3, -2, -3, 2, 3, -2, -3, \dots$

Het is wel een beetje saai. Probeer zelf maar iets spannenders uit (periode $7$ of zo).

Bonusvraag Denk je dat de waarde van $k$ hier beperkt moet zijn tot gehele getallen?

Probeer zelf eens $k = 3{,}5$ en beredeneer wat je dan eigenlijk aan het doen bent. De recepten voor rijtjes kunnen soms heel complex worden. Als laatste voorbeeld geven we het volgende recept. Dit recept is extra lastig, want het hangt af van of het volgende getal op een even of oneven plek terecht komt in de rij!

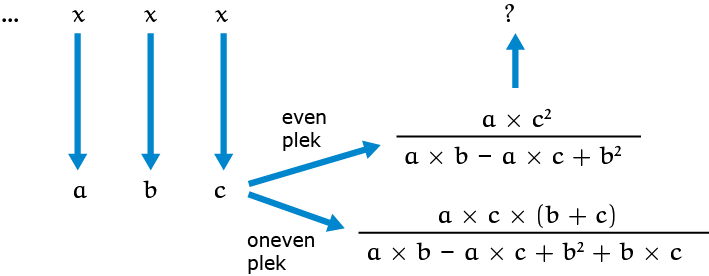
Berekening van zo'n rij vraagt wel een rekenmachine of een programma waarin je dat berekent. Hieronder staat een uitgewerkt rekenvoorbeeld, met begin-getallen $1, 1{,}2$ en $1{,}5$:

Stap	$a$	$b$	$c$	volgende
$1$	$1{,}00000$	$1{,}20000$	$1{,}50000$	$1{,}37755$
$2$	$1{,}20000$	$1{,}50000$	$1{,}37755$	$0{,}95004$
$3$	$1{,}50000$	$1{,}37755$	$0{,}95004$	$0{,}86207$
$4$	$1{,}37755$	$0{,}95004$	$0{,}86207$	$1{,}00000$
$5$	$0{,}95004$	$0{,}86207$	$1{,}00000$	$1{,}20000$
$6$	$0{,}86207$	$1{,}00000$	$1{,}20000$	$1{,}50000$
$7$	$1{,}00000$	$1{,}20000$	$1{,}50000$	$1{,}37755$
$8$	$1{,}20000$	$1{,}50000$	$1{,}37755$	$0{,}95004$

enzovoorts.

Uiteindelijk krijg je dus de rij:

$$1{,}00000; 1{,}200000; 1{,}50000; 1{,}37755; 0{,}95004; 0{,}86207; 1{,}00000; 1{,}20000; 1{,}500000; 1{,}37755; \dots$$

Wat lijkt? Hier heb je dus een rij, geconstrueerd met behulp van ingewikkelde quotiënten van tweede en derdegraads polynomen in $a$, $b$ en $c$. En de periode is $6$? Dat is natuurlijk wel verdacht mooi. Hoe kan dat? Eerst checken we rekenfouten, maar elke keer is de periode 6.

Als je precies dezelfde berekening doet maar dan met behoud van breuken, dus zonder afrondingen naar decimale schrijfwijze zoals hierboven, dan krijg iets dat sommigen nog veel interessanter zullen vinden. Het laat zien dat de periode echt $6$ is. We schrijven $\frac{6}{5}$ in plaats van $1{,}2$ en $\frac{3}{2}$ in plaats van $1{,}5$:

$$1,\frac{6}{5}, \frac{3}{2}, \frac{135}{98}, \frac{1350}{1421}, \frac{25}{29}, 1, \frac{6}{5}, \frac{3}{2}, \dots$$

Zes is geen toeval: ook voor andere $a$, $b$, $c$ krijg je die periode. Bijvoorbeeld $a = 1$, $b = \frac{1}{2}$, $c = \frac{1}{4}$:

$$1,\frac{1}{2}, \frac{1}{4}, \frac{3}{10}, \frac{6}{5}, 2, 1, \frac{1}{2}, \frac{1}{4}, \dots$$

Hoe kan het dat zo’n supercomplex recept leidt tot zo’n eenvoudige periode $6$? Dit is een mooi voorbeeld van hoe concrete formules je het zicht kunnen ontnemen op een mooie oplossing. Hoe formules het lastig kunnen maken, waardoor de oplossing van deze vraag eigenlijk een beetje verborgen zit. Dat komt door uitdrukkingen

$$\frac{a\times c^2}{a\times b - a\times c+b^2}$$en$$ \frac{a\times c\times(b+c)}{a\times b-a\times c+b^2+b\times c}$$

Die uitdrukkingen komen niet zomaar uit de lucht vallen maar die krijg je als uitkomst van de vraag naar de oppervlakte van de driehoek met $d$ in de volgende figuur, als de oppervlaktes $a$, $b$ en $c$ gegeven zijn. De eerste formule correspondeert met positie van $a$, $b$, $c$, $d$ in de linker driehoek, de onderste formule met de rechter driehoek. De formules uitrekenen vraagt geduld en is zeker wat gedoe maar wezenlijk niet lastig: niks meer dan elementaire kennis over de oppervlakte van een driehoek in termen van basis en hoogte (probeer zelf; het linker geval is relatief makkelijk; het rechter geval is echt lastiger).

Dus de tabel met de ingewikkelde formules hierboven is meetkundig niks meer dan het bij elke stap linksom rondlopen in een driehoek met $6$ kleinere driehoekjes, waar de drie 'vorige' oppervlaktes al gegeven zijn, en elke keer de goeie formule kiezen. Dat daar een periode 6 uitkomt is dan zeer beredeneerbaar, want het volgt uit de meetkundige constructie. Hier helpt elementaire meetkunde dus de interpretatie van een lastig rijtjesprobleem, want het is helemaal niet zo simpel de periode $6$ op een directe algebraïsche manier af te leiden uit de formules

$$\frac{a\times c^2}{a\times b - a\times c+b^2}$$en$$ \frac{a\times c\times(b+c)}{a\times b-a\times c+b^2+b\times c}.$$

Over dit soort getallenrijen is een hoop te vragen. Zijn er oplossingen met alleen gehele getallen? Hoeveel? In een volgend nummer gaan we in op een aantal eigenschappen van deze rijen.