Het draaibeertje waar het in dit stukje om draait, is niét ontworpen door de Hongaar Ernő Rubik, maar door Emmanuel Carrillo, een industrieel ontwerper en een Rubik’s cube wizard, zoals hij zichzelf op zijn website omschrijft. Het beertje bestaat uit zes elementen: de linker- en rechterhelften van de kop, de linker- en rechterhelften van de romp, en de beide achterpoten. De voorpoten vormen een geheel met de helften van de romp. Houden we het rechteroor van het beertje vast, dan kunnen de elementen op drie manieren ten opzichte van elkaar worden gedraaid. De gehele linkerhelft kan met een halve slag ondersteboven worden gekeerd, de romp kan met een halve slag achterstevoren worden gedraaid, en de achterpoten kunnen met een halve slag achterstevoren worden gedraaid.

Een schema met alle beertjes

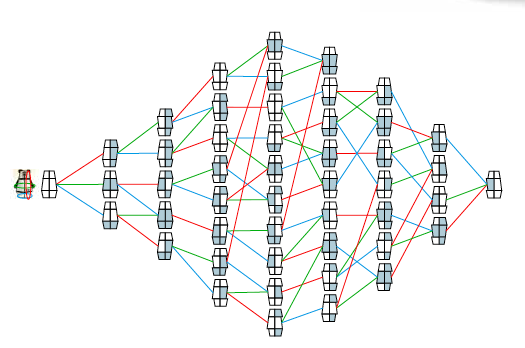
Met proberen en enig ruimtelijk inzicht kun je 48 verschillende verschijningsvormen tellen. Het diagram in figuur 1 laat zien hoe ze in elkaar overgaan. Een rode lijn betekent een halve slag van de linkerhelft (voor de kijker rechts), een groene lijn een halve slag van de romp, en een blauwe lijn een halve slag van de poten. De lijnen lopen vanzelfsprekend in beide richtingen. De figuur vertelt welke beertjes er bestaan, en met welke opeenvolging van halve slagen het ene beertje in het andere verandert. Tussen het onvervormde beertje links en het meest rechtse beertje zijn er minstens acht halve slagen nodig. 

Het beertje als graaf

Het diagram in figuur 1 is een zogenaamde ‘graaf ’. Een graaf bestaat uit punten (de toestanden van het beertje) verbonden door lijnen (de halve slagen). Met deze graaf kun je gemakkelijk aflezen hoe je van elke toestand in elke andere toestand kunt komen. Kun je een route bedenken waarbij je alle toestanden één keer langskomt?

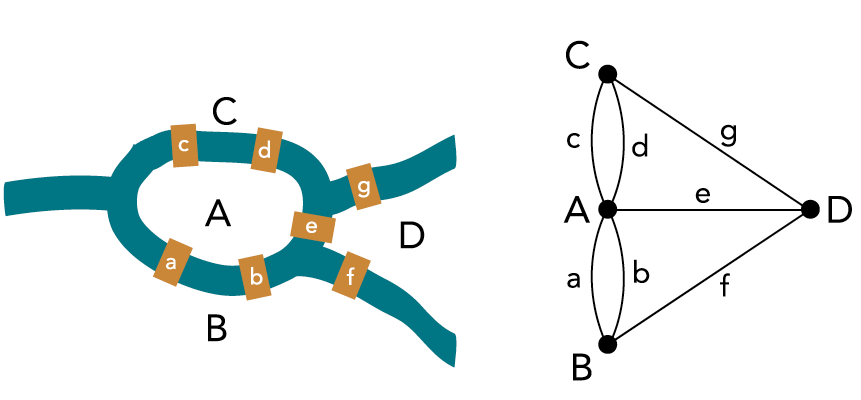
De Zwitserse wiskundige Leonhard Euler stelde zich rond 1736 een soortgelijke vraag voor de bruggen in de stad waar hij woonde. Hij dacht na over de zeven bruggen over de takken van de rivier de Pregel in de stad Koningsbergen (nu Kaliningrad). Bestaat er een wandelroute waarlangs je alle bruggen achtereenvolgens eenmalig oversteekt? Euler modelleerde de oevers en het door de rivier omsloten eilandje met punten, en de bruggen met lijnen tussen deze punten (zie figuur 2). Hij maakte een begin met het onderzoek van dergelijke structuren, en bewees dat je de gewenste wandeling op geen enkele manier kunt maken.

Voor onze beertjesgraaf is er een soortgelijke vraag, waarin niet de lijnen maar de punten centraal staan: bestaat er een opeenvolging van halve slagen waarmee alle beertjes achtereenvolgens verschijnen, zonder dubbelingen? Zoiets heet een Hamiltonpad.

 

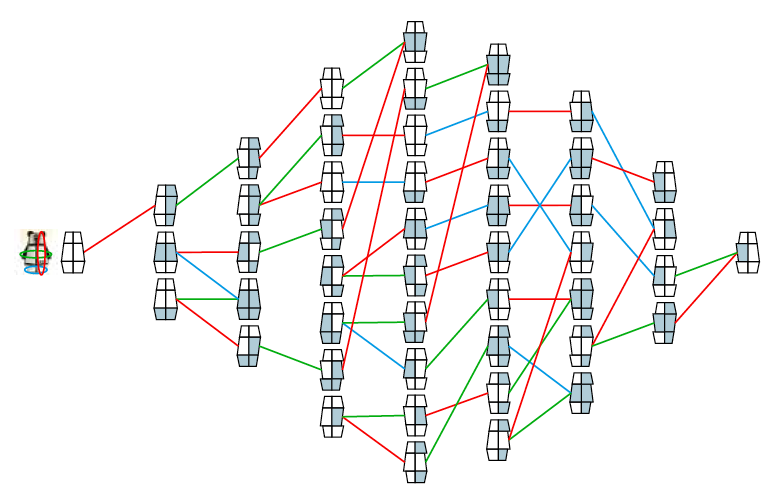
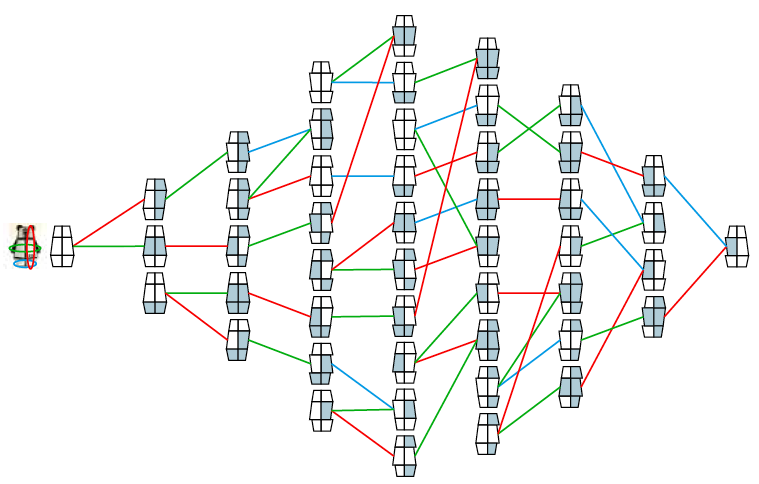
Kun je dan met nog één halve slag extra weer bij het oorspronkelijke beertje uitkomen? Zo’n volgorde heet een Hamiltoncykel. In het algemeen vergt het vinden van zo’n pad veel rekenkracht. Omgekeerd is het natuurlijk eenvoudig om vast te stellen of een bepaald pad of een bepaalde cykel wel of niet ‘Hamiltoniaans’ is. De beertjesgraaf blijkt zowel Hamiltonpaden als -cykels te hebben. De diagrammen in de figuren 3 en 4 geven van elk een voorbeeld.

Rekenen met het beertje

In het vervolg vatten we de halve slagen op als transformaties die het beertje omvormen. We noteren ze op grond van hun kleur in de graaf met $R$(ood), $G$(roen) en $B$(lauw). Het is belangrijk om op te merken dat de definities van $R, G$ en $B$ niet afhangen van de toestand van het beertje. Dit betekent dat, hoewel voor ons gevoel het onvervormde beertje een voorkeursplaats heeft, bij nader inzien alle beertjes gelijkwaardig zijn. Maar juist daarom beperken we ons niet als we enkel vanuit het onvervormde beertje redeneren.

Het verdraaien van het beertje komt neer op het na elkaar toepassen van de transformaties $R, G$ en $B,$ in eindige aantallen en in verschillende volgordes. De samenstelling $G \circ B \circ R \circ B$ moet je dus als volgt lezen: ‘voer eerst $B,$ dan $R,$ daarna weer $B,$ en ten slotte $G$ uit’. We spreken het uit als ‘$G$ na $B$ na $R$ na $B$ ’.

Laten we nu eens kijken naar de draaiingen en niet naar de beertjes. De graaf geeft aan dat elk beertje kan worden getransformeerd tot 47 andere beertjes. Met de halve slagen $R, G$ en $B$ kunnen we met inbegrip van de identieke transformatie I die het beertje intact laat, 48 verschillende transformaties voortbrengen.

Als je goed naar figuur 1 op pagina 6 kijkt, kun je allerlei gelijkheden ontdekken, bijvoorbeeld

$$B \circ R \circ B \circ G \circ B \circ R \circ B = R \circ G \circ R.$$

We zien ook dat ‘$B$ na $G$ ’ en ‘$G$ na $B$ ’ hetzelfde zijn, ofwel $B \circ G = G \circ B$. Dit is bij ingewikkeldere vormen, zoals Rubiks kubus, al niet meer zo. We zeggen dat $G$ en $B$ commuteren. We kunnen dat gebruiken voor ingewikkeldere formules als

$$G \circ B \circ R \circ B = B \circ G \circ R \circ B.$$

Groepen

De graaf drukt in feite uit hoe we kunnen rekenen met de samenstellingen van $R, G$ en $B.$ Uit elk tweetal van de 48 transformaties ontstaat, volgens de rekenregels vastgelegd in de graaf, een andere transformatie, die ook weer één van die 48 is. Zo komen we tot een tweede gedachtesprong. Het gaat niet om de draaiingen, maar het draait om de rekenregels. De transformaties van het beertje vormen met hun rekenregels een zogenaamde ‘groep’.

Een groep is een algebraïsche structuur waarin het rekenen associatief is (dat betekent dat het niet uitmaakt hoe je de haakjes zet: $G \circ (B \circ R)$ geeft hetzelfde resultaat als $(G \circ B) \circ R)$, er een neutraal element is (hier is dat $I),$ en waarin elk element een inverse ten opzichte van dat neutrale element heeft.

Laten we dat laatste nog even nagaan voor het beertje. Een halve slag tweemaal uitgevoerd brengt het beertje onveranderd terug, ofwel

$$R \circ R = G \circ G = B \circ B = I.$$

Dus $R, G$ en $B$ zijn hun eigen inverse. Ook elke samenstelling heeft een inverse. De inverse van $G \circ B \circ R \circ B$ is de omkering $B \circ R \circ B \circ G$. Immers:

$$(G \circ B \circ R \circ B) \circ (B \circ R \circ B \circ G) =$$

$$G \circ B \circ R \circ (B \circ B) \circ R \circ B \circ G =$$

$$G \circ B \circ R \circ I \circ R \circ B \circ G =$$

$$G \circ B \circ R \circ R \circ B \circ G =$$

$$G \circ B \circ B \circ G = G \circ G = I,$$

en evenzo in de andere volgorde:

$$(B \circ R \circ B \circ G) \circ (G \circ B \circ R \circ B) = I.$$

Het spelen met Rubiks beer is dus eigenlijk hetzelfde als het rekenen volgens speciale regels. Het aantal elementen en de rekenregels leggen de groep helemaal vast. Het blijkt dat er 52 verschillende groepen van 48 elementen zijn. Zouden we daar allemaal beertjes, of ander speelgoed, voor kunnen bedenken?