Een van de opgaven van de eerste ronde van de Wiskunde Olympiade luidde als volgt. 

Zet de getallen 1 t/m 15 op een rij, zo dat twee getallen naast elkaar steeds optellen tot een kwadraat. Wat is de uitkomst als we het eerste en laatste getal bij elkaar optellen? 

In dit artikel beschrijven we een programma geschreven in Python waarmee je dit probleem kunt oplossen. Maar het kan nog veel meer. In plaats van kwadraten kun je ook kiezen voor derdemachten of driehoeksgetallen (dat zijn de sommen $1 + 2 + 3 + \cdots + n$). We gaan uit van een willekeurige (eindige) verzameling $S$. Je wilt de getallen $N = {1, 2, 3, \ldots, n}$, voor zekere $n$ rangschikken zo dat elk van de sommen van twee opeenvolgende getallen een element is van $S$. De notatie werkt met "$\ -\ $" tussen de getallen. Bijvoorbeeld voor $n = 6$ en $S = {7, 8}$ vinden we de oplossing $1 - 6 - 2 - 5 - 3 - 4$. Deze oplossing is (op volgorde na) uniek.

Vooraf

Om te beginnen bepalen we de verzameling $S$. Dit gebeurt in Programma 1. Uiteraard kun je lukraak een aantal getallen kiezen die samen $S$ vormen, maar je kunt er ook voor kiezen om de derde machten in $S$ te plaatsen. Ook is het mogelijk om de Fibonaccigetallen in $S$ te plaatsen, of een combinatie van verschillende soorten getallen.

VerschiLlEnde GetalLen

De uitkomst van het programma dat we schrijven is een reeks $n_1 - n_2 - \ldots - n_k$, waarbij ${n_1, n_2, \ldots , n_k}$ een bepaalde permutatie is van getallen ${1, 2, 3, \ldots , k}$. We merken op dat de getallen $n_1$ en $n_k$ één buur hebben en de overige getallen twee buren. De volgende opsplitsing van de getallen ${1, 2, 3, \ldots , k}$ ligt dus erg voor de hand: 

• Geïsoleerde getallen. Verzameling C0 (aantal is $c0$). Een getal $k$ is bevat in C0 als er geen enkel getal $m \in N$ te vinden is met $k + m \in S$.
• Getallen met slechts één buur. Verzameling C1 (aantal is $c1$). Een getal $k$ is bevat in C1 als er precies één getal $m \in N$ bestaat met $n + m \in S$.
• De overige getallen hebben twee of meer buren. (Deze getallen zijn niet bevat in een verzameling met een specifieke naam.)

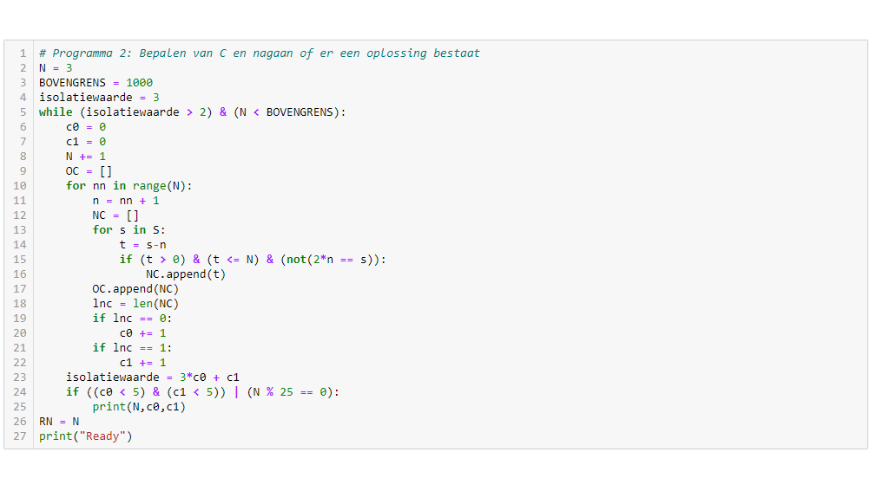
We gaan eerst uitzoeken voor elk getal of het betreffende getal bevat is in C0 of C1. Het is duidelijk dat je zelfs als $c0 = 1$ geen keten kunt maken. Ook moet $c1$ beperkt zijn (tot hooguit $2$).

Dit alles controleren we in Programma 2. Dan volgt Programma 3. Hier gaan we aan de slag met getallen die precies twee buren hebben. We beginnen met de getallen ${1, 2, 3, \ldots, N}$, die in eerste instantie elk een keten van lengte 1 vormen. Alle getallen worden geplaatst in Sin. Successievelijk worden ketens aan elkaar gekoppeld. Er ontstaan middengetallen (Mid) en randgetallen (Ran). De administratie is best wel lastig als twee ketens worden gekoppeld. Uiteindelijk blijft er één keten over met $2$ randgetallen en verder middens. 

De precieze werking staat beschreven in het programma zelf. (Kijk op hieronder bij [Documenten]).

Voorbeeld

We nemen een nog eenvoudiger voorbeeld dan de kwadraten. We kiezen de driehoeksgetallen (de sommen $1 + 2 + 3 + \cdots + n$). $N = {1, 2, 3, \ldots, 10}$. Het eerste dat we gaan doen is voor de getallen $1$ t/m $10$ nagaan of er een single tussen zit, en welke getallen op de rand terecht gaan komen. 

$S = {1, 3, 6, 10, 15}$. Het volgende element zou $21$ zijn, maar $9 + 10 = 19$ is de grootste som die gemaakt kan worden. Vervolgens gaan we alle buren bepalen:

$\color{\white}{n}$	$\color{\white}{buren\ van\ n}$	$\color{\white}{stukje\ keten}$
$1$	$2, 5, 9$
$\color{\white}{2}$	$\color{\white}{1, 4, 8}$
$3$	$7$	$3 - 7$
$\color{\white}{4}$	$\color{\white}{2, 6}$	$\color{\white}{2 - 4 - 6}$
$5$	$1, 10$	$1 - 5 - 10$
$\color{\white}{6}$	$\color{\white}{4, 9}$	$\color{\white}{4 - 6 - 9}$
$7$	$3, 8$	$3 - 7 - 8$
$\color{\white}{8}$	$\color{\white}{2, 7}$	$\color{\white}{2 - 8 - 7}$
$9$	$1, 6$	$1 - 9 - 6$
$\color{\white}{10}$	$\color{\white}{5}$	$\color{\white}{10 - 5}$

We zien dat $3$ en $10$ aan de rand komen. Vervolgens gaan we kijken naar getallen met precies twee buren. Mocht er een keten zijn, dan vormt dat getal met die twee buren een deel van de keten. Deze stukjes keten bevatten twee eindpunten. Bovendien kunnen getallen die precies twee buren hebben elders ook op de rand voorkomen. Dat is reden om de stukjes keten te vergroten. Bijvoorbeeld geldt dat voor $4$, $5$ en $6$.

We bekijken in een nieuwe tabel stukjes keten en de buren van de betreffende stukjes keten:

$\color{\white}{keten}$

$1-5-10$

$\color{\white}{2-4-6-9-1}$

$3-7-8-2$

Nu is het een kwestie om de drie deelketens met elkaar te verbinden. We vinden: $3 - 7 - 8 - 2 - 4 - 6 - 9 - 1 - 5 - 10$. 

In het deel onder [Documenten] (zie hieronder) worden ook ingewikkeldere situaties uitgelegd. Maar het basisidee blijft hetzelfde: je bouwt een totale keten op door steeds meer deelketens met elkaar te verbinden. Het programma biedt ook de mogelijkheid om te tellen hoeveel verschillende ketens er zijn, of om na te gaan dat er ook cykels bestaan (hierbij zijn er geen begin- en eindpunten).

Opgave 1 Voer de opdracht uit van de Wiskunde Olympiade. Opgave 2 Laat $S$ de verzameling van getallen van de vorm $n^2 + 1$ zijn. Bepaal het kleinste aantal getallen waarvoor er een keten bestaat. Opgave 3 Toon aan dat als $S$ uit even getallen bestaat er geen keten bestaat. In principe kan het voorkomen dat alle getallen twee of meer buren hebben. Opgave 4 Gebruik de programmatuur om een keten te vinden voor de volgende gevallen: Fibonaccigetallen (het is niet zo moeilijk om meerdere ketens te vinden) Derdemachten (dit is niet meer met de hand te doen!)