Elk jaar wordt in Nederland de CodeCup georganiseerd. Dit is een wedstrijd waarbij computerprogramma's een spel tegen elkaar moeten spelen. Dit jaar is het spel gebaseerd op een wiskundig spel dat in de jaren 60 populair was op universiteiten in Amerika.

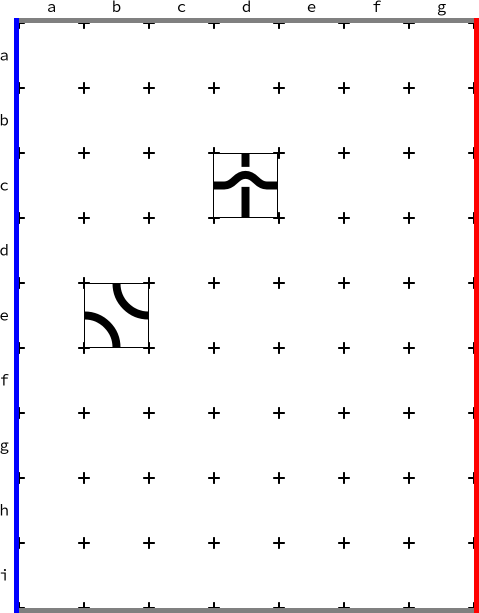
Spaghetti is een spel voor twee spelers; blauw en rood. Je speelt het op een rechthoekig bord dat bestaat uit $9\times 7$ vakjes. De linkerzijde van het bord heeft een blauwe rand en hoort bij de blauwe speler. De rechterzijde
van het bord heeft een rode rand en hoort bij de rode speler. Elk vakje heeft twee coördinaten die worden aangegeven met een letter (figuur 1). 

De spelers leggen om de beurt een stukje op het bord. Het neerleggen van een stukje op een specifieke locatie noemen we een 'zet'. De stukjes zijn vierkant en hebben twee segmenten erop getekend die twee zijden met elkaar verbinden. Er zijn dan  ook maar drie soorten stukjes. Die stukjes geven we als naam 'links', 'rechtdoor' en 'rechts'. 

De naam van het stukje geeft aan of het segment dat vanaf de linkerzijde binnenkomt linksaf ($l$), rechtdoor ($s$) of rechtsaf ($r$) gaat. Er zijn ongelimiteerd veel stukjes van elke soort. 

Je kunt een zet beschrijven met drie letters. De eerste twee letters  geven de coördinaten aan van het vakje waar het stukje gelegd wordt, de laatste letter geeft aan welk stukje is geplaatst.

Om het spel interessant te maken begint het spel altijd met twee zetten van de jury. De jury zet twee stukjes op (tamelijk) willekeurige plaatsen op het bord. De jury zorgt dat deze stukjes nooit een zijkant aanraken. In figuur 1 zie je een mogelijk  spelbord om mee te beginnen. De jury heeft zetten $cds$ en $ebr$ gedaan. 

Winnen

Het doel van het spel is om één of meer paden te vormen die de rode en blauwe zijde met elkaar verbinden. De speler die de zet doet waardoor een pad compleet wordt gemaakt krijgt punten voor dit pad. Als je een zet doet waardoor een cykel ontstaat (dat is een pad dat naar zichzelf terugkeert), of als je een zet doet waardoor een pad ontstaat dat twee zijdes van dezelfde kleur verbindt krijg je strafpunten. De speler die de meeste punten heeft aan het einde van het spel wint. 

Score

Elke speler begint met 50 punten. Wanneer je een zet doet die een pad van de blauwe zijde naar de rode zijde compleet maakt dan krijg je net zoveel punten als het aantal segmenten van het laatst geplaatste stukje naar jouw zijde van het bord. Je begint segmenten te tellen in het laatst geplaatste stukje bij het segment dat zo ver mogelijk van je zijde vandaan ligt.

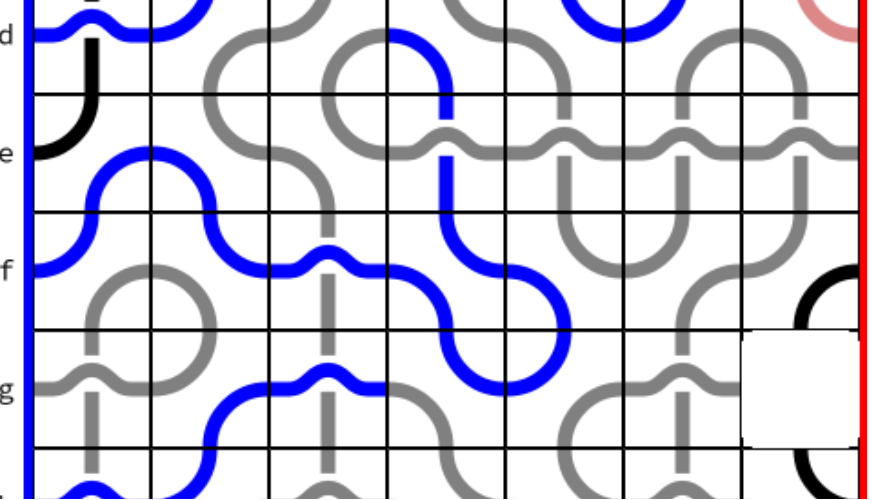
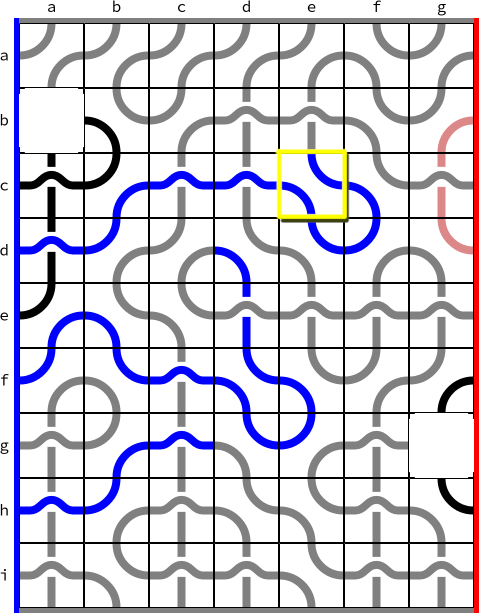
Figuur 3 geeft een voorbeeld van een spelsituatie waarbij blauw de laatste zet heeft gedaan. Deze zet, $cer$, is in het plaatje met een gele rand gemarkeerd. Hierdoor wordt de blauwe zijde vanaf da verbonden met de rode zijde in $ag$. Omdat dit stukje is geplaatst door de blauwe speler krijgt deze 10 punten. Als rood in hun beurt dit pad had afgerond zou rood hiermee 11 punten hebben verdiend.

Als er door je zet een cykel ontstaat dan krijg je 5 strafpunten. 
Als er door je zet een pad ontstaat dat van een gekleurde zijde terug gaat naar dezelfde gekleurde zijde, dan krijg je 3 strafpunten. Het maakt in dit geval niet uit om welke gekleurde zijde het gaat; als blauw krijg je zowel strafpunten voor een verbinding van blauw naar blauw, als een verbinding van rood naar rood.
Het is mogelijk dat je in één zet twee paden, twee cykels, of zowel een pad als een cykel maakt. In dit geval worden de eventuele (straf)punten voor beide paden of cykels meegeteld.

Proberen

Als je met een spelletje aan de slag gaat is het slim om het eerst zelf te proberen. Dit is op een ruitjesvel makkelijk te doen. Je kunt op codecup.org het spel ook spelen tegen een computerspeler die niet nadenkt en maar wat doet. Je kunt dan op het scherm goed zien hoe het scoreverloop is. 
Paden die verbonden zijn met een niet gekleurde zijde zijn grijs, want daar kunnen nooit punten of strafpunten aan verbonden
zijn. Paden die zwart zijn gekleurd kunnen nog een bijdrage leveren aan de puntentelling. Paden die een donkere kleur  ebben
leveren punten op voor de speler van die kleur. Lichtgekleurde paden leveren strafpunten op voor de speler van die kleur.
In de situatie in figuur 3 is de score voor blauw $50 + 10 + 12 + 4 = 76$ punten, en heeft rood $50 - 3 = 47$ punten.

Programmeren

Als je het spel uitgeprobeerd hebt, en je denkt dat je wel een leuke manier hebt bedacht om punten te scoren, is het tijd om
jouw strategie te programmeren. Je kunt je strategie dan inzenden bij de CodeCup om te zien hoe goed je het doet ten opzichte van andere programma's. 

Als je het programma schrijft moet je met de jurysoftware communiceren; je krijgt telkens informatie van de jury over welke zet er gedaan is, en jij moet dan een nieuwe zet bepalen die je vertelt aan de jury. De jury geeft die zet dan door aan het programma van je tegenspeler. De jurysoftware vertelt je altijd eerst wat de twee zetten van de jurysoftware zijn. Als je programma als derde instructie 'Start' doorkrijgt, dan ben je de blauwe speler en mag je beginnen. Als je als derde instructie een zet doorkrijgt dan ben je de rode speler. Elke keer dat je aan de beurt bent lees je dus de laatste zet van je tegenstander, en geef je als uitvoer welke zet jij daarna doet. 

Ik beschrijf nu hoe je een heel eenvoudig Python3 programma kunt maken dat telkens een willekeurige zet doet. Je mag je programma ook in een andere programmeertaal schrijven; je vindt meer details op de website. 

Als je het programma schrijft moet je zelf bijhouden wat de toestand van het bord is. Je mag dit doen zoals je zelf wilt. In dit voorbeeld gebruik ik een dictionary als datastructuur waarbij ik voor de gevulde vakjes bijhoud welk stukje erin is gezet. De  sleutel voor de dictionary is telkens de coördinaat van het vakje.

bord = {}

Verder is het ook fijn om een precies lijstje te hebben met welke vakjes nog niet zijn gevuld en welke stukjes ik mag gebruiken:

beschikbaar = [ x + y for x in "abcdefg" for y in "abcdefghi" ]
   stukjes = [ 'l', 's', 'r' ]

Hierna begin je natuurlijk met het inlezen van de twee vakjes die door de jury worden gevuld. Omdat we later ook zetten  moeten inlezen heb ik hiervoor een functie geschreven: 

def leeszet():
   global bord, beschikbaar
   x, y, stukje = list(input())
   bord[x+y] = stukje
   beschikbaar.remove(x + y)

Ik kan de juryzetten nu simpel inlezen door twee keer leeszet() aan te roepen: 

leeszet()
leeszet()

Nu wordt het iets moeilijker. Ik krijg nu namelijk een instructie door waarop ofwel een zet staat, ofwel het woord 'Start'. Ik pas nu mijn functie $leeszet()$ aan om een zet alleen te verwerken als het daadwerkelijk een zet is:

def leeszet():
   global bord, beschikbaar
   regel = input()
   if regel != 'Start':
      x, y, stukje = list(regel)
      bord[x + y] = stukje
      beschikbaar.remove(x + y)

Dit maakt het mogelijk om dit voorbeeldprogramma heel simpel te houden. Ik lees eerst twee zetten in die aangeven welke
stukjes de jury heeft geplaatst. Daarna ga ik door met instructies inlezen zolang er nog beschikbare vakjes zijn:

leeszet()
leeszet()
while beschikbaar:
   leeszet()
   if beschikbaar:
      zet = bepaalzet()
      print(zet)

Tenslotte moet ik natuurlijk nog de functie $bepaalzet()$ schrijven die bepaalt welke zet mijn programma gaat doen. Omdat ik in dit voorbeeld een willekeurige zet wil doen moet ik aan het begin van het programma een extra module importeren om random (willekeurige) dingen te kunnen doen:

import random

Met behulp van deze module kan ik een willekeurig element uit een lijst kiezen en zo dus eenvoudig de computer laten  bepalen welke zet wordt gedaan: 

def bepaalzet():
   global bord, beschikbaar, stukjes
   coordinaat = random.choice(beschikbaar)
   stukje = random.choice(stukjes)
   bord[coordinaat] = stukje
   beschikbaar.remove(coordinaat)
   return coordinaat + stukje

Mijn simpele programma is nu compleet. Wanneer het speelt tegen een programma dat serieus nadenkt zal mijn programma
niet veel punten verdienen. Kun jij het beter? Welke slimme dingen kun je bedenken om een zo hoog mogelijke score te
halen? Is de datastructuur die ik gebruik wel slim gekozen, of moet je iets anders bedenken om de lengte van de paden ook
makkelijk te kunnen bepalen? 

Tips

Je hoeft niet in een keer je beste programma te maken. Er zijn meerdere rondes die na elkaar worden gespeeld. Je kunt na een ronde precies zien hoe jouw programma heeft gespeeld tegen andere spelers, om vervolgens te analyseren wat je anders zou kunnen doen. Daarna kun je dus verbeteringen doorvoeren in je programma en een nieuwe versie inzenden voor de volgende ronde. 

Het aantal mogelijke coördinaten waar je uit kunt kiezen op het speelbord is $7 \cdot 9$; hier moet je de twee jury vakjes nog vanaf trekken. Dan resteren er dus $61$ mogelijke posities voor je eerste zet. Je kunt telkens kiezen uit exact $3$ stukjes. In totaal zijn er dus $3 \cdot 61 = 183$ mogelijkheden voor je eerste zet. Het aantal mogelijke zetten neemt telkens af. Als je dus maar één zet vooruit kijkt heb je helemaal niet zoveel tijd nodig.

Je kunt bijvoorbeeld een programma schrijven dat eerst kijkt of je een zet kunt doen die een pad afmaakt, en dan automatisch
die zet doet. Als je geen pad kunt afmaken ga je op zoek naar een zet die zo min mogelijk strafpunten oplevert. Je zou ook kunnen kijken of je een programma kan maken dat het juist goed doet tegen een tegenstander die met deze strategie speelt.

Onderzoek 

Het totaal aantal verschillende spelletjes is $63! \cdot 3^{63}$, dat is ongeveer $2 \cdot 10^{117}$. Het is dus onmogelijk om alle mogelijke  spelletjes uit te laten rekenen. Kun je een slimme methode bedenken om zoveel mogelijk spelletjes te winnen? Of kun je  misschien beredeneren welke speler altijd kan winnen? Aan het einde van de CodeCup zullen we hier laten weten welke programma's het beste waren en welke strategieën de deelnemers hadden gekozen.

doe mee! 

Als je mee wilt doen moet je zelf een computerprogramma schrijven dat Spaghetti kan spelen. Dat programma kun je zo makkelijk of moeilijk maken als je zelf wilt. Ga naar codecup.org voor meer informatie over de regels en het protocol om met de jury software te communiceren.