Voor de tweede ronde worden de winnaars van de eerste ronde uitgenodigd, die eind januari op alle deelnemende scholen plaatsvindt. Uiteraard zijn de opgaven bij de tweede ronde weer van een niveau hoger dan bij de eerste ronde. De deelnemers hebben bijvoorbeeld hun hoofd gebroken over het zo efficiënt mogelijk vullen van een $3\times 2$-rechthoek met de getallen $1$ tot en met $6$, in de zin dat de zeven onderlinge verschillen tussen buurgetallen in totaal zo klein mogelijk moet zijn. Ook was er een vraag over een vierkant waarop steeds kleinere vierkantjes groeien zodat er een fractal-achtig figuur ontstaat; probeer daar maar eens de omtrek van te berekenen… Deze en alle andere opgaven zijn terug te vinden op www.wiskundeolympiade.nl in het Wedstrijdarchief. De tweede C-opgave ging over getallen die voor de gelegenheid zonnige getallen waren gedoopt.

		Opgave C2 - tweede ronde 2022 We noemen een positief geheel getal zonnig als het uit vier cijfers bestaat en als bovendien elk van de twee buitenste cijfers precies 1 groter is dan het cijfer ernaast. De getallen $8723$ en $1001$ zijn bijvoorbeeld zonnig, maar $1234$ en $87245$ zijn dat niet.  Hoeveel zonnige getallen zijn er waarvan het dubbele ook weer een zonnig getal is? Bewijs dat elk zonnig getal groter dan $2000$ deelbaar is door een getal van drie cijfers dat een $9$ in het midden heeft.

Om een beetje vertrouwd te raken met zo'n nieuw begrip, kan het geen kwaad eens te bedenken hoeveel zonnige getallen er überhaupt zijn. Een manier om dit te zien, is als volgt: de middelste twee cijfers kun je vrij kiezen, bijvoorbeeld (van links naar rechts) $a$ en $b$; dan liggen het eerste (meest linkse) en laatste cijfer automatisch vast (namelijk $a + 1$ respectievelijk $b + 1$). Elk zonnig getal is dus van de volgende vorm:

Voor $a$ (en ook voor $b$) zijn er in eerste instantie tien mogelijkheden ($0$ tot en met $9$), maar omdat $a + 1$ ook een cijfer moet zijn, valt $a = 9$ af. We concluderen dat er voor $a$ dus negen opties zijn ($0$ tot en met $8$) en idem voor $b$, wat ons in totaal $9 \cdot 9 = 81$ zonnige getallen geeft. Wat we hierbij even onder het tapijt hebben geschoven, is dat een getal natuurlijk nooit met het cijfer $0$ mag beginnen. Maar dat gaat hier automatisch goed omdat $a + 1$ sowieso minstens $1$ is.

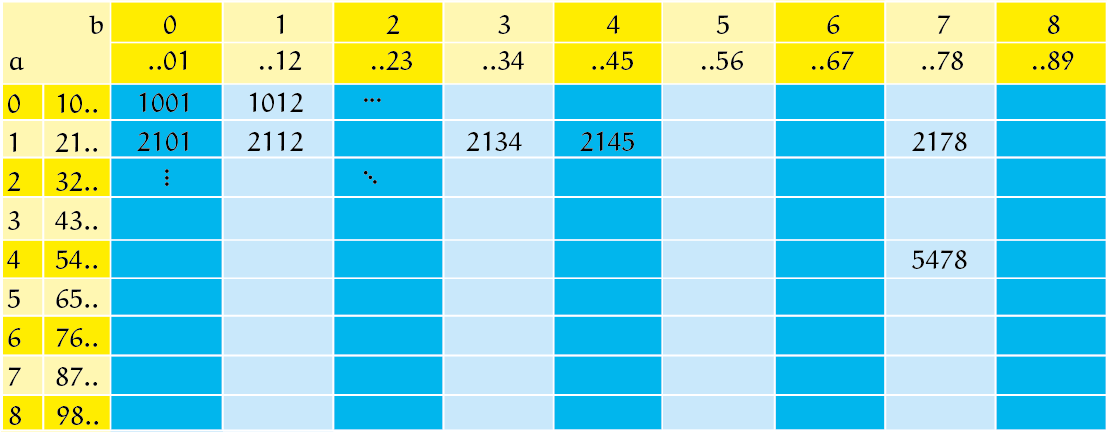
Een tabEl met 81 zonNige getaLlen? Dat kAn sliMmer!

We zouden nu onderdeel (a) kunnen oplossen door daadwerkelijk een tabel met alle $81$ zonnige getallen op te schrijven (hierboven is een overzichtelijk beginnetje gemaakt), van elk van deze getallen het dubbele uit te rekenen, en dan telkens te kijken of dat weer een zonnig getal is. Dat zou zeker tellen als een volledige oplossing; erg elegant is het alleen niet en bovendien zou het best wel veel tijd kosten. Vandaar deze variant op het bekende spreekwoord: wie geen tijd heeft, moet slim zijn! Om daarbij de goede ideeën te krijgen, gaan we een paar voorbeelden bekijken. Een van de manieren om je in een probleem te verdiepen is immers: durf te proberen!

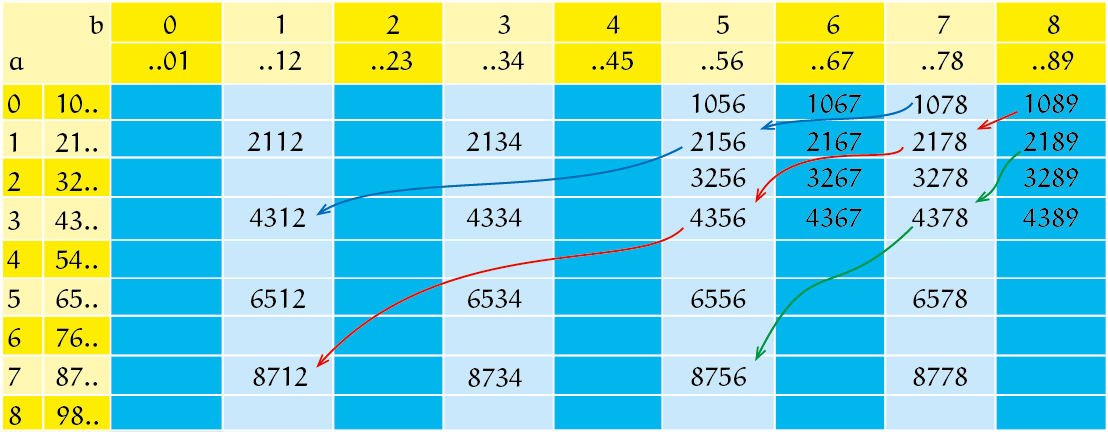
Neem een willekeurig zonnig getal, bijvoorbeeld $2134$. Het dubbele daarvan is $4268$; dat is verre van een zonnig getal. En we krijgen meteen ons eerste goede idee: eigenlijk is het ook wel logisch dat het hier 'misgaat', want de cijfers worden verdubbeld en dus wordt het verschil tussen de laatste twee cijfers nu $2$ (en het verschil tussen de eerste twee cijfers trouwens ook in dit voorbeeld). Dit argument gaat op voor alle zonnige getallen die eindigen op $..01$, $..12$, $..23$ of $..34$, want dan eindigt het dubbele hiervan op $..02$, $..24$, $..46$ of $..68$ zodat de uitkomst hoe dan ook geen zonnig getal is. Kortom, als $0 \le b \le 3$, dan krijgen we zeker niet een zonnig getal na verdubbeling. Daarmee hebben we dus direct al $9 \cdot 4 = 36$ van de $81$ getallen afgestreept; de hele linkerkant van bovenstaande tabel.

We bekijken een volgend voorbeeld: $2145$. Het dubbele hiervan is $4290$ en dat is zeker niet zonnig. We realiseren ons dat elk zonnig getal dat op $..45$ eindigt, na verdubbeling op $..90$ eindigt en dus zeker niet zonnig is. De hele kolom $b = 4$ uit bovenstaande tabel valt dus ook weg, waarmee er nog eens $9$ getallen zijn afgestreept.

We bedenken een nieuw voorbeeldje waarbij de laatste twee cijfers allebei groter dan $4$ zijn, zodat er minstens twee keer een $1$ gaat overspringen bij het verdubbelen. Hoe zit het bijvoorbeeld met het zonnige getal $2178$? Daarvan is het dubbele $4356$, en dat is wel zonnig! Yes, we hebben een zonnig getal gevonden dat 'het doet'. We hebben hier blijkbaar te maken met twee gunstige overspring-enen: het dubbele van $8$ is $16$, waarvan de $1$ samen met $14$ (het dubbele van $7$) leidt tot een $5$ op de plek van de tientallen zodat het resultaat eindigtop $..56$. En die $1$ van $14$ leidt samen met het dubbele van $21$ tot $43$.. aan het begin van het getal. Zowel aan het begin als aan het eind is het buitenste cijfer dus $1$ hoger dan het binnenste cijfer. In welke gevallen doet dit fenomeen zich nog meer voor? Dat is als het zonnige getal eindigt op $..56$, $..67$, $..78$ of $..89$; dan is het dubbele namelijk $112$, $134$, $156$ respectievelijk $178$, zodat het wat de laatste twee cijfers betreft wel goed zit. En bovendien komt de $1$ er bij de honderdtallen bij, zodat voor zonnige getallen die beginnen met $10..$, $21..$, $32..$ of $43..$ het resultaat na verdubbeling begint met $21..$, $43..$, $65..$ of $87..$, en het dus wat de eerste twee cijfers betreft ook goed gaat. We hebben hiermee $4 \cdot 4 = 16$ zonnige getallen gevonden waarvoor de gevraagde eigenschap wel geldt; om precies te zijn als $0 \le a \le 3$ en $5 \le b \le 8$, de rechterbovenhoek van bovenstaande tabel.

We hebben alleen de rechter onderhoek nog over en bekijken dus maar eens een zonnig getal dat met een $5$ of hoger begint, zoals $5478$. Daarvan is het dubbele $10\,956$, een getal van vijf cijfers in plaats van vier, dus dat gaat sowieso mis (hoe leuk die $56$ op het eind ook is). Kortom, de zonnige getallen met $4 \le a \le 8$ (zodat het eerste cijfer $a + 1 \ge 5$) kunnen we ook afschieten, want dan bestaat het resultaat na verdubbeling uit te veel cijfers. Daarmee vervalt ook het hele onderste deel van bovenstaande  tabel (waarvan we de eerste vijf kolommen natuurlijk al eerder hadden afgestreept). We concluderen dat er precies $16$ zonnige getallen bestaan waarvan het dubbele ook weer zonnig is. Zoals bij elk wiskundig probleem waar je alle oplossingen moet vinden, moesten we hier twee dingen laten zien: dat er $16$ zonnige getallen zijn waarvoor dit zo is, en bovendien dat de overige $81 - 16 = 65$ zonnige getallen deze eigenschap juist niet hebben.

Altijd deelbaar door *9*

Onderdeel (b) gaat over de $8 \cdot 9 = 72$ zonnige getallen die groter dan $2000$ zijn, dus de getallen met $1 \le a \le 8$ en $0 \le b \le 8$. Meteen moet er een alarmbelletje bij je afgaan, of — beter gezegd — juist een lampje bij je aangaan: waarom zou deze extra voorwaarde hier eigenlijk staan? Ongetwijfeld heb je die later ergens nodig! Hoe dan ook, als deze uitspraak waar is, dan zou het ons moeten lukken om het in ieder geval in afzonderlijke voorbeelden te laten zien. Dus laten we weer eens een voorbeeldje bekijken. Kunnen we het getal $2134$ schrijven als een product van twee getallen waarvan eentje tussen de $100$ en de $999$ ligt met een $9$ als middelste cijfer? Omdat dat driecijferige getal minstens $100$ is, moet de andere deler hooguit $2134/100 = 21{,}34$ en dus zelfs hooguit $21$ zijn. Laat we dus proberen om $2134$ door een kleine deler te delen en dan te hopen dat we $*9*$ als quotiënt over houden. Het getal is even, dus deelbaar door $2 : 2134 = 2 \cdot 1067$, maar hier is het quotiënt niet van de gewenste vorm. Door $3$ is het niet deelbaar, en door $5$ of $7$ evenmin. Hetvolgende priemgetal dat we proberen is $11$, en dat geeft een hit: $2134 = 11 \cdot 194$; ons zonnige getal is deelbaar door $11$ en het quotiënt is een driecijferig getal met een $9$ in het midden! Hoe zit dat met $2178$? Dat is niet alleen deelbaar door $2$ en $3$ (met als quotiënten $1089$ en $726$, dus niet van de gewenste vorm), maar ook weer door $11$, waarbij we vinden dat $2178 = 11 \cdot 198$. Volgend voorbeeld: $5478$. Ja hoor, ook dat kunnen we door $11$ delen: $5478 = 11 \cdot 498$. Het lijkt wel of elk zonnig getal door $11$ deelbaar is. Zelfs zonnige getallen kleiner dan $2000$, bijvoorbeeld $1012 = 11 \cdot 92$. We zetten de eerste drie voorbeelden even op een rij:

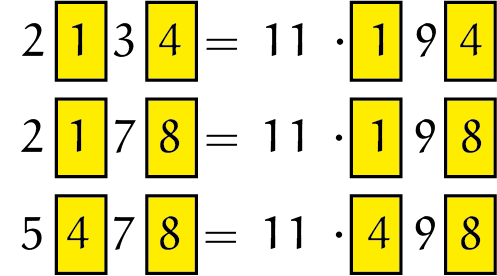
Wiskunde is soms ook: patroonherkennen. In deze drie gevallen zien we dat de honderdtallen van ons zonnige getal en het gevraagde quotiënt overeenkomen, evenals het laatste cijfer (de eenheden). Dus als ons zonnige getal uit de cijfers $a + 1$, $a$, $b$ en $b + 1$ bestaat zoals we eerder invoerden, dan bestaat in deze drie voorbeelden het quotiënt bij deling door $11$ uit $a$, $9$ en $b + 1$. Maar dat dat in deze drie voorbeelden zo is, wil nog niet zeggen dat het voor alle $72$ zonnige getallen groter dan $2000$ geldt. Ook hier zouden we weer een lijst met al deze kunnen maken en telkens het quotiënt kunnen uitrekenen. Maar ook nu weer kunnen we slimmer te werk gaan. We gaan bewijzen dat

In plaats van de deling door $11$ uit te voeren, berekenen we juist het product van de twee getallen uit de rechterkant en bewijzen we dat dit het linker getal als uitkomst heeft. Het getal bestaande uit de cijfers $a$, $9$ en $b+1$ is, wegens de rol van deze cijfers als honderdtallen, tientallen en eenheden, niets anders dan de uitkomst van de berekening $a \cdot 100 + 9 \cdot 10 + (b + 1) \cdot 1$, oftewel $100a + 91 + b$. Doen we dat keer $11$, dan krijg je $11 \cdot (100a+91+b)$, oftewel $1100a + 11 \cdot 91 + 11b = 1100a + 11b + 1001$. Nu is $1100a + 11b$ precies het getal bestaande uit de cijfers $a$, $a$, $b$ en $b$, en tellen we daar nog $1001$ bij op, dan krijgen we precies ons zonnige getal bestaande uit de cijfers $a + 1$, $a$, $b$ en $b + 1$. Dus kunnen we omgekeerd elk zonnig getal bestaande uit de cijfers $a + 1$, $a$, $b$ en $b + 1$ ontbinden als $11$ maal het getal bestaande uit de cijfers $a$, $9$ en $b + 1$. Hiermee hebben we het gevonden patroon bewezen! 

En waarom stond die voorwaarde er nou bij? Als $a$ gelijk is aan $0$, dan zou dat quotiënt beginnen met het cijfer $0$. Maar dan is het natuurlijk geen getal van drie cijfers meer! Toch geldt de bewezen ontbinding natuurlijk nog steeds; zo is $1001 = 11 \cdot (0)91$ en $1067 = 11 \cdot (0)97$. 

Deze laatste twee voorbeeldjes kunnen, hoewel ze dus eigenlijk niet meedoen, overigens ook goede ideeën opleveren om te zien dat de ontbinding altijd opgaat. Want van $1001$ naar $1067$ is een toename van $66$, en dat is $6 \cdot 11$, dus als de één deelbaar is door $11$, is de ander dat zeker ook. En van $1001$ naar bijvoorbeeld $2134$ is een toename van $1133$, en dat is $11 \cdot 103$ dus ook weer een $11$-voud. Tellen we $103$ op bij $91$ (het quotiënt van 1001 bij deling door 11), dan komen we uit op 194 (het quotiënt van 2134 bij deling door 11). Omdat deelbaarheid door 11 in ieder geval voor één zonnig getal geldt (1001) en er steeds een 11-voud bijkomt (dat moet je dan natuurlijk nog wel even netjes bewijzen), weet je nu zeker dat elk zonnig getal deelbaar is door 11. En met nog wat meer argumenten kun je ook wat zeggen over hoe dat quotiënt er dan uit ziet.

Een getal is zelfs superzonnig

In onderdeel (a) hadden we gezien dat voor precies $16$ zonnige getallen geldt dat het dubbele weer zonnig is. Laten we dit de $16$ bijzonder zonnige getallen noemen; die zitten in de rechterbovenhoek van eerdergenoemde tabel. Behoort dat dubbele zonnige getal nou zelf ook weer tot die $16$ bijzonder zonnige getallen, dan is zelfs het viervoud van het oorspronkelijke zonnige getal weer zonnig. Dit geldt voor de vier zonnige getallen $1078$, $1089$, $2178$ en $2189$. En als het viervoud ook weer bijzonder zonnig is, is zelfs het achtvoud van het oorspronkelijke zonnige getal weer zonnig. Er is precies een getal waarvoor dit geldt, namelijk $1089$. Dat wil dus zeggen dat $1089$, het dubbele $2178$, het dubbele daarvan $4356$ en het dubbele daar weer van $8712$ allemaal zonnig zijn! Als dat geen superzonnig getal is… En alsof dat nog niet spectaculair genoeg is: zelfs de andere (viercijferige) veelvouden van $1089$ zijn allemaal zonnig! Zo is $7 \cdot 1089$ bijvoorbeeld gelijk aan $7623$. Hoe kan dat nou weer? We kunnen de resterende veelvouden natuurlijk gemakkelijk even uitrekenen: $3 \cdot 1089 = 3267$, $5 \cdot 1089 = 5445$, $6 \cdot 1089 = 6534$ en $9 \cdot 1089 = 9801$. We zien dat we inderdaad telkens een zonnig getal als uitkomst krijgen; sterker nog, dat dit precies de zonnige getallen op de diagonaal van rechtsboven naar linksonder van onze tabel zijn. Maar het is nóg leuker om ook een reden te vinden waarom dit werkt. Je kan $1089$ schrijven als $1100 - 11$. Ga nu uit van een getal op die diagonaal, bijvoorbeeld $3267$. Tel je hier $1100$ bij op, dan krijg je $4367$, en trek je er ook nog $11$ van af, dan krijg je $4356$; het volgende getal op de diagonaal! Door deze twee acties blijft inderdaad de zonnigheid behouden zolang de cijfers nog netjes tussen de $0$ en de $9$ zitten, want als de eerste twee cijfers in eerste instantie $1$ verschillen, doen ze dat natuurlijk nog steeds nadat we ze beide eentje hoger maken, en als de laatste twee cijfers in eerste instantie $1$ verschillen, doen ze dat natuurlijk nog steeds nadat we ze beide eentje lager maken. Zo kun je van het getal rechtsboven ($1089$) naar het getal linksonder ($9801$) lopen waarbij je telkens het volgende zonnige getal op deze diagonaal tegenkomt. En omdat je dan in feite met $1089$ begint en er telkens $1089$ bij optelt, doorloop je dus eigenlijk gewoon de tafel van $1089$.