Het eerste deel van de wedstrijd bestaat uit acht vijfkeuze-opgaven; het tweede deel bevat acht open vragen. De opgaven gaan onder meer over patronen, breuken, gehele getallen en figuren in het platte vlak of de ruimte. Wat ze in ieder geval gemeen hebben, is dat je er een flinke dosis gezond verstand en doorzettingsvermogen voor nodig hebt om ze op te lossen. En dan ook nog eens binnen de beperkte tijd van $45$ minuten voor elk van beide delen. We bekijken in dit artikel een opgave uit deel $2$.

JUNIOR WISKUNDE OLYMPIADE 2018, DEEL 2, OPGAVE 7

Zes gelijkzijdige en even grote driehoeken worden aan elkaar geplakt tot een parallellogram $ABCD$, zie figuur $1$. 

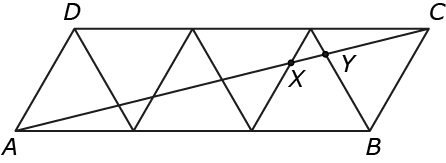
De lengte van $AC$ is $10$. Wat is de lengte van $XY$? 

Het plaatje is opgebouwd uit zes gelijkzijdige driehoeken die allemaal even groot zijn. Als we de lengte van de zijde van deze driehoeken even $a$ noemen, dan zien we dat $AD = BC = a$ en $AB = CD = 3a$. Naast deze lengtes weten we ook de hoeken van het parallellogram $ABCD$: die zijn $60^o$ bij $A$ en $C$, en $120^o$ bij $B$ en $D$, omdat daar twee van de gelijkzijdige driehoeken samenkomen. 
Er zijn meerdere wegen die tot het antwoord leiden. We bekijken hier twee mogelijke aanpakken. Bij de eerste aanpak moet behoorlijk worden gerekend en heb je de stelling van Pythagoras nodig. De tweede aanpak is veel elementairder en veel minder foutgevoelig, maar doet wel een groter beroep op je inzicht en creativiteit.

Stug doorrekenen

De punten $X$ en $Y$ zijn de snijpunten van gegeven lijnen in dit plaatje, zodat we op zoek zouden kunnen gaan naar de vergelijkingen van deze lijnen als we de oorsprong bijvoorbeeld in $A$ kiezen en $AB$ als de positieve $x$-as. We lopen dan wel tegen een paar (deel)probleempjes aan: wat is eigenlijk de richtingscoëfficiënt van een lijn die een hoek van $60^o$ maakt met de $x$-as (zoals $AD$ en de lijn door $X$)? En hoe groot is de richtingscoëfficiënt van lijn $AC$? Daarnaast moet je nog uitrekenen wat $a$ is, gegeven dat $AC$ gelijk is aan $10$. Als je hier allemaal uitgekomen bent én de juiste vergelijkingen van de relevante lijnen hebt gevonden én daarmee ook nog eens zonder rekenfouten de coördinaten van de snijpunten $X$ en $Y$ gevonden hebt, kun je het uiteindelijke antwoord op de vraag vinden met behulp van de Stelling van Pythagoras (met wederom kans op een rekenfout). Die stelling had je trouwens ook al nodig gehad om de helling van $AD$ te bepalen en om af te leiden wat $a$ is; zie hieronder.

Schets van de rekenoplossing

We stellen $A(0, 0)$ en $B(3a, 0)$. De $x$-coördinaat van $D$ is $\frac{1}{2}a$, dus uit de Stelling van Pythagoras volgt dat $D$ op een hoogte van $$\sqrt{a^2-\left(\frac{1}{2}a\right)^2}=\frac{1}{2}\sqrt{3}\,a$$ ligt: $$D\left(\frac{1}{2}a,\frac{1}{2}\sqrt{3}\,a\right).$$ Om van $A$ naar $D$ te komen moet je dus $\frac{1}{2}a$ naar rechts en $\frac{1}{2}\sqrt{3}\,a$ omhoog, wat betekent dat de richtingscoëfficiënt van $AD$ gelijk is aan $$\frac{\frac{1}{2}\sqrt{3}\,a}{\frac{1}{2}a}=\sqrt{3}.$$ Het punt $C$ ligt op dezelfde hoogte, maar hiervoor moet je juist $3a+\frac{1}{2}a=\frac{7}{2}a$ naar rechts vanuit $A$: $$C\left(\frac{7}{2}a,\frac{1}{2}\sqrt{3}\,a\right).$$ De helling van $AC$ is dus $$\frac{\frac{1}{2}\sqrt{3}\,a}{\frac{7}{2}a} = \frac{1}{7}\sqrt{3}.$$ Nu je de coördinaten van $C$ weet, kun je met de Stelling van Pythagoras ook de lengte van $AC$ in termen van $a$ vinden: $$AC=\sqrt{\left(\frac{7}{2}a\right)^2 + \left(\frac{1}{2}\sqrt{3}\,a\right)^2} = \sqrt{13}\,a.$$ Door deze lengte gelijk te stellen aan $10$ vinden we dat $$a=\frac{10}{\sqrt{13}}=\frac{10}{13}\sqrt{13}.$$ Om $X$ te vinden moet je het snijpunt bepalen van de lijn $y=\frac{1}{7}\sqrt{3}\,x$ en de lijn $y=\sqrt{3}(x-2a)$, terwijl het voor $Y$ juist om de lijnen $y=\frac{1}{7}\sqrt{3}\,x$ en $y=-\sqrt{3}\,(x-3a)$ gaat. Als we dat doen en bovendien de waarde van $a$ invullen, vinden we dat $$X\left(\frac{70}{39}\sqrt{13},\frac{10}{39}\sqrt{39}\right)$$ en $$Y\left(\frac{105}{52}\sqrt{13},\frac{15}{52}\sqrt{39}\right).$$ Voor de horizontale en verticale afstand tussen $X$ en $Y$ vinden we hiermee dat $$\Delta x=\frac{105}{52}\sqrt{13}-\frac{70}{39}\sqrt{13} = \frac{35}{156}\sqrt{13}$$ en $$\Delta y=\frac{15}{52}\sqrt{39} - \frac{10}{39}\sqrt{39} = \frac{5}{156}\sqrt{39}.$$ Daaruit volgt ten slotte dat $$XY=\sqrt{(\Delta x)^2+(\Delta y)^2} = \frac{1}{156}\sqrt{16900} = \frac{5}{6}.$$

Evenwijdige lijnen

Je kunt het probleem echter ook oplossen zonder zulke rekenpartijen. Hiervoor loont het de moeite om nog eens goed het plaatje te bestuderen en te kijken of je wat opvalt. Zo zijn er wegens de regelmaat van de figuur diverse evenwijdige lijnen te ontdekken. In figuur $2$ zie je alle lijnen die evenwijdig aan $AD$ lopen in rood aangegeven.

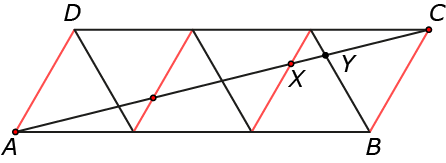
De vier rode lijnen lopen niet alleen evenwijdig, maar liggen ook nog eens op onderling telkens dezelfde afstand; ze gaan immers door de vier punten die lijnstuk $DC$ in drie gelijke stukken verdelen (waarbij elk stuk de zijde van een van de gelijkzijdige driehoeken is). Maar dat betekent dat ze lijnstuk $AC$ net zo goed in drie gelijke stukken verdelen! Dat is in te zien aan de hand van de drie snavelbekdriehoeken bestaande uit $\angle DCA$ en één van de drie linker rode lijnen als tegenoverliggende zijde. Deze verhouden zich als $1 : 2 : 3$, waarbij de grootste van de drie $\triangle DCA$ is. Hieruit volgt dat $XC$ drie keer zo klein is als $AC$, dus $XC=\frac{1}{3}\cdot 10$. Merk op dat de rode lijnen het hele parallellogram $ABCD$ in feite opdelen in drie even grote ruiten, die elk bestaan uit twee van de zes gelijkzijdige driehoeken.

Het punt $Y$ ligt, behalve op lijn $AC$, ook op een lijn waaraan nog twee lijnen in ons plaatje evenwijdig lopen; laten we deze groen kleuren. Kunnen we aan de hand hiervan misschien ook iets over $YC$ zeggen? Vergelijkbaar met hierboven bevinden zich tussen de groene lijnen weer twee even grote ruiten, maar we blijven wel met twee “halve ruiten” aan weerszijden zitten. Niets weerhoudt ons er echter van om ons plaatje uit te breiden met nóg eens twee gelijkzijdige driehoeken, zodat we uiteindelijk vier even grote ruiten naast elkaar krijgen. Dat zie je in figuur $3$.

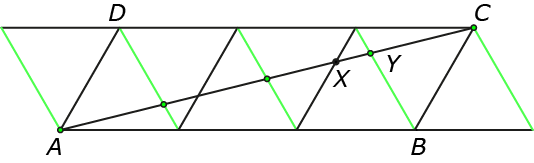
Op deze manier zien we vier gelijkvormige snavelbekdriehoeken die alle hoekpunt $C$ gemeen hebben en waarvan de zijde tegenover $C$ een van de vier linker groene lijnen is. Deze verhouden zich als $1 : 2 : 3 : 4$, waaruit volgt dat $YC$ vier keer zo klein is als $AC$, dus $YC = \frac{1}{4}\cdot 10$. 

Nu we $XC$ en $YC$ kennen, is het niet moeilijk meer om $XY$ uit te rekenen:

$$ XY = XC - YC = \frac{1}{3}\cdot 10 - \frac{1}{4}\cdot 10 = \left(\frac{1}{3} - \frac{1}{4}\right) \cdot 10 = \left( \frac{4}{12} - \frac{3}{12} \right)\cdot 10 = \frac{1}{12}\cdot 10 = \frac{10}{12}=\frac{5}{6}$$

Zonder grote rekenpartijen en met louter elementaire middelen zijn we bij het antwoord uitgekomen, en wel door eerst even goed naar het plaatje te kijken in plaats van meteen te gaan rekenen. Daardoor zagen we evenwijdige lijnen en vervolgens gelijkvormige driehoeken. 

Terugblik

We hebben bij de tweede aanpak het antwoord gevonden zonder eerst de zijde van de gelijkzijdige driehoeken te hoeven berekenen. Dat was blijkbaar een tussenstap (in de eerste oplossing) die helemaal niet nodig was. Ook de lengte van $AC$ blijkt eigenlijk van ondergeschikt belang (ook al is deze natuurlijk wel van invloed op je eindantwoord); uit de tweede oplossing blijkt dat de lengte van $XY$ namelijk hoe dan ook $1/12$ deel is van de lengte van $AC$, wat $AC$ ook is. Dit is iets wat we ook vooraf hadden kunnen opmerken: als we het plaatje onder een kopieerapparaat leggen en met een bepaalde factor vergroten (of verkleinen), dan worden alle lengtes in het plaatje met diezelfde factor vergroot, dus verandert de verhouding van $XY : AC$ niet. We hadden ons dus in eerste instantie op deze verhouding kunnen richten, en om die te vinden hadden we best wel mogen aannemen dat $AC$ gelijk aan $1$ is, of juist dat de gelijkzijdige driehoeken zijdelengte $a = 1$ hebben (wat de rekenoplossing iets behapbaarder had gemaakt: in plaats van $X\left(\frac{70}{39}\sqrt{13},\frac{10}{39}\sqrt{39}\right)$ hadden we dan $X\left(\frac73,\frac13\sqrt3\right)$ gevonden). Zo hadden we $XY$ en ook $AC$ kunnen uitrekenen en daarmee de verhouding $XY : AC$ gevonden, die we dan natuurlijk nog wel even met $10$ hadden moeten vermenigvuldigen om het antwoord op de juiste vraag te geven.  

Eerste ronde

Ben je benieuwd naar de rest van de opgaven van de Junior Wiskunde Olympiade? Kijk dan op www.wiskundeolympiade.nl in het Wedstrijdarchief. Heb je zin om zelf in wedstrijdverband aan zulke puzzels te werken? Geef je dan op bij je wiskundedocent voor de eerste ronde van de Wiskunde Olympiade, die van 21 t/m 31 januari 2019 plaatsvindt op alle deelnemende scholen en openstaat voor iedereen uit klas 1 t/m 5 die wel houdt van een wiskundige uitdaging!