De laatste maanden spelen Milli en Mu een breinbreker op hun telefoon en verzamelen daarbij punten. Dat aantal punten kan negatief zijn, bijvoorbeeld als ze een dag niet gespeeld hebben of fouten maakten. Dit is de reeks scores van Mu over de laatste twaalf dagen:

De app houdt bij wat je beste streak* is: een aaneengesloten periode van dagen met de hoogste totaalscore. Ze wilden graag weten hoe de app dat doet, want met die negatieve scores leek dat best lastig. Mu vond het een voor de hand liggend idee om alle aaneengesloten periodes door te rekenen. Dat deed Mu als volgt in Python (de code is ook te vinden via de knop [Bekijk oplossing] onderaan de pagina):

Let op dat in Python de uitdrukking de scores van dag tot en met dag aanduidt, dus zonder . Bij de scores van het voorbeeld komt de streak op 16 punten, wat de som is van .

Het programma van Mu is best eenvoudig. Phi kon het echter niet nalaten om te vragen hoe efficiënt het is. Een manier om die efficiëntie te meten is om te tellen hoeveel rekenstappen er nodig zijn. Er zijn veel verschillende soorten rekenstappen, maar je krijgt een goede indruk door te tellen hoe vaak een score in de lijst wordt opgezocht. Milli leek het een goed idee om dat aantal door het programma zelf te laten tellen. Daartoe voegde Milli aan het programma een variabele toe, die op $0$ start en die telkens wanneer wordt berekend, verhoogd wordt met . Na het verwerken van de twaalf scores uit het voorbeeld staat die teller op $364$. En na het verwerken van het dubbele aantal is dat al opgelopen tot $2600$. Als je handig in wiskunde bent, dan kun je beredeneren dat als er $N$ scores zijn, de teller eindigt op $N(N + 1)(N + 2)/6$, wat altijd een geheel getal is. (Snap je waarom het altijd geheel is?) Dus bij verdubbeling van $N$ wordt het aantal stappen ongeveer $2^3 = 8$ keer zo groot. Voor $N = 1000$ is het aantal stappen al meer dan honderd miljoen.

Milli zag al snel in dat het telkens opnieuw sommeren van een periode veel dubbel werk met zich meebrengt. Want als één groter wordt, dan is de periode één dag langer en kun je de som van de vorige periode verhogen met de score van de dag die er bij komt. Dat leidt tot het volgende programma, inclusief de teller:

Het programma van Milli heeft voor het verwerken van de twaalf scores uit het voorbeeld nog maar $78$ stappen nodig en voor het dubbele aantal scores $300$. Het is nu wat makkelijker om de formule te vinden: voor $N$ scores kost het $N(N + 1)/2$ stappen. Een verdubbeling van $N$ kost dan nog maar ongeveer $2^2 = 4$ keer zoveel stappen. Dat is een flinke verbetering.

Mu had wat zitten toekijken en er borrelde een sluw idee op om Milli te verslaan. Mu was destijds zeer onder de indruk van binair zoeken, waarbij je het probleem telkens halveert. Hier kan dat niet echt, maar Mu opperde dat als je het probleem in twee helften verdeelt, je die helften apart kan oplossen en dan de oplossingen kan samennemen. Stel je verdeelt in twee zo gelijk mogelijke delen, zeg en . Je bepaalt nu de streak van beide delen en neemt daar de beste van. Het kan zijn dat het nog beter kan door een periode te bekijken die deels in en deels in ligt. Maar als dat zo is, dan is dat een nietleeg staartstuk van , samen met een niet-leeg beginstuk van . Het beste staartstuk van en het beste beginstuk van zijn eenvoudig te bepalen.

Hier is het programma van Mu, met , gedefinieerd als Python functie die je aanroept met :

Dat is niet meer een programma waarvan je eenvoudig inziet dat het correct is. Het is een recursief algoritme, dat wil zeggen de functie  roept zichzelf aan (maar alleen als er meer dan één score is). Is het wel efficiënter? De twaalf scores uit het voorbeeld worden in $56$ stappen verwerkt en die van het dubbele aantal in $136$. Ja, dus. Het is ook niet zo eenvoudig om in te zien dat het totaal aantal stappen bij $N$ scores in de orde van $N \log(N)$ ligt. Verdubbeling van $N$ geeft iets meer dan een verdubbeling van het aantal stappen. En het is dus zelfs behoorlijk wat efficiënter dan Millis programma.

Pi was diep onder de indruk dat Mu dit voor elkaar had gekregen, maar suggereerde dat het toch nog beter kon. Ideaal zou het zijn als elke score maar precies één keer wordt bekeken, want beter dan dat is natuurlijk onmogelijk. Dan kost het voor $N$ scores nog maar $N$ stappen. En verdubbeling van het aantal scores betekent ook verdubbeling van het aantal stappen.

Daar moesten Milli en Mu wel even van slikken. Hoe zou je dat voor elkaar kunnen krijgen? Pi gaf toen als hint dat een belangrijk idee voor een lineaire oplossing al besloten lag in het recursieve programma van Mu, waarin het beste staartstuk een rol speelt. Daarop begon bij Milli iets te dagen. Als je van een beginstuk van alle scores weet wat de beste streak is, en je dat beginstuk uitbreidt met een nieuwe score, dan kan de beste streak die je had, alleen verslagen worden door een staartstuk dat eindigt met die nieuwe score. En het nieuwe beste staartstuk bepalen als je het vorige beste staartstuk al kent is ook eenvoudig. Milli schreef het als volgt op (de teller was nu niet meer nodig):

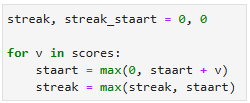
Waar je voor moet opletten is dat negatief kan zijn. In dat geval begin je weer met een lege staart. Dat is precies wat de uitdrukking doet. Iedereen was het er snel over eens dat dit programma eenvoudig, elegant en efficiënt is. Maar niet iets waar je meteen op komt.

 

		Volgende keer Het is je vast opgevallen dat de illustratie van de familie boven elk artikel anders is. Wat is het algoritme achter de volgorde van de familieleden in die illustratie?

 

* Een streak is de periode van de hoogste score. Wat hier steeds berekend wordt is de score zelf in die periode. Dat is het moeilijkst om te berekenen. Als je die eenmaal hebt is het bepalen van de periode zelf makkelijk.

 

Bekijk oplossing