Je bent jarig, je hebt vijf vrienden uitgenodigd, en voor het feest van vanavond een grote appeltaart gebakken. Van twee mensen weet je alleen niet zeker of ze wel komen. Aafke moest vanochtend naar de kaakchirurg en als ze ’s avonds nog veel last van haar kaak heeft, zal ze niet naar je feest komen. Bart is de hele week al grieperig, dus of hij erbij kan zijn, is ook allerminst zeker. Kortom: het bezoek kan uit drie, vier of vijf personen bestaan.

Het gedoe met het aansnijden van de taart wil je voorkomen waar het bezoek bij is. Dus het snijden doe je vooraf. Maar je houdt niet van restjes. Bovendien wens je dat iedereen – elke bezoeker én jijzelf – evenveel krijgt. Kun je dan toch vooraf de taart aansnijden? 

Natuurlijk! Als je de taart in 60 $(= \frac{1}{2} \times 4 \times 5 \times 6)$ stukjes snijdt, dan kun je op het moment dat de visite er is, de stukjes taart verdelen over de aanwezigen (inclusief jouzelf zijn dat vier, vijf of zes personen). Als je de taartpuntjes over vier personen moet verdelen, dan krijgt iedereen 15 stukjes. Zijn er vijf personen aanwezig, dan krijgt iedereen 12 stukjes en als iedereen komt, dan krijgt elk 10 stukjes. Maar dit levert heel wat snijwerk op. Kan het ook met minder?

Als je eerst zelf wilt bedenken in hoeveel stukjes je de taart minimaal moet verdelen om hem uiteindelijk eerlijk te kunnen verdelen onder vier, vijf of zes personen, lees dan nu nog niet verder. 

Met de niet zo efficiënte methode die we net bespraken, is elk taartpuntje 1/60 deel van de hele taart. We gaan nu op een slimme manier deze kleine stukjes taart weer samenvoegen.

In figuur 1 is de taart schematisch weergegeven als een rechthoek van 6 $\times$ 10. Je kunt sowieso een stuk taart ter grootte van 1/6 afsnijden, ofwel 10 stukjes. Mochten er 5 eters zijn, dan wil je dit stuk taart aanvullen met 2 stukjes taart tot 12 stukjes (namelijk 1/5 deel) en als er 4 eters zijn, dan wil je het stuk taart aanvullen met 5 stukjes taart tot 15 stukjes (namelijk 1/4 deel). Hoe krijg je dit voor elkaar? Snij 3 maal een stuk van 1/6 deel van de taart af (blauw), 4 maal een stuk van 1/12 deel van de taart (groen) en ten slotte kun je het resterende 1/6 deel verdelen in 5 gelijke delen, dus elk 1/30 deel (rood). In totaal heb je dan 12 stukken.

Het kan beter!

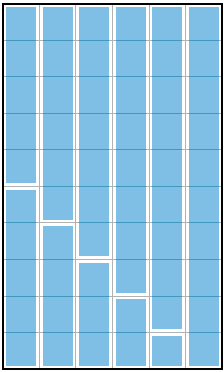
In figuur 2 is onze schematische taart gesneden in slechts 11 stukken. Deze hebben een grootte van 1/60, 2/60, 3/60, 4/60, 5/60, 5/60, 6/60, 7/60, 8/60, 9/60 en 10/60 (let op: 5/60 komt dubbel voor). Na vereenvoudiging van de breuken heb je taartdelen van 1/60, 1/30, 1/20, 1/15, 1/12, 1/12, 1/10, 7/60, 2/15, 3/20 en 1/6. Het is mogelijk om deze 11 stukken samen te voegen tot 6 maal 1/6 stuk taart, 5 maal 1/5 stuk of 4 maal 1/4 stuk. Kun je zelf bedenken hoe?

Algemeen

Het snijden van de taart op een zo efficiënt mogelijke manier mag een leuke puzzel zijn, het is ook serieus voer voor wiskundigen. Diverse onderzoekers zijn op zoek naar de optimale verdeling van een taart als er maximaal n personen zijn. We hebben gezien dat je voor $n = 6$ de taart niet in meer dan 11 delen hoeft te snijden. Kun je ook bedenken waarom het met minder dan 11 delen niet lukt?

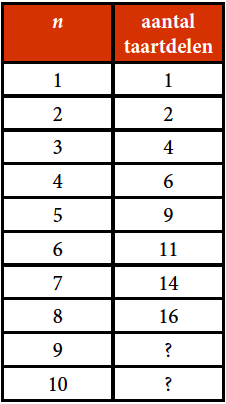
Het is verbazingwekkend dat dit probleem voor $n = 9$ al erg moeilijk is. Tot nu toe heeft niemand kunnen uitrekenen wat het kleinste aantal taartdelen is als $n$ groter is dan 8. In de onderstaande tabel staan de resultaten die momenteel bekend zijn (zie ook de rij A265286 in de Online Encyclopedia of Integer Sequences).