Toen Hans Kuiper de oproep van Henk Rusman zag dacht hij meteen aan een van zijn bestaande ontwerpen (zie figuur 1).

In een ver verleden was hij tot dit ontwerp gekomen door de afbeeldingen in een boek over fractals uit te proberen en daarmee verder te experimenteren.

Achteraf is zonder veel wiskunde met een paar gedachtesprongen ook tot dit ontwerp te komen. Zeker als bekend is dat Hans Kuiper zijn ontwerp indertijd Conform schaakbord noemde. Neem een normaal schaakbord met 64 velden (8 bij 8 dus, met 81 hoekpunten).

Neem aan dat het van rubber is zodat het gemakkelijk vervormd en uitgerekt kan worden.

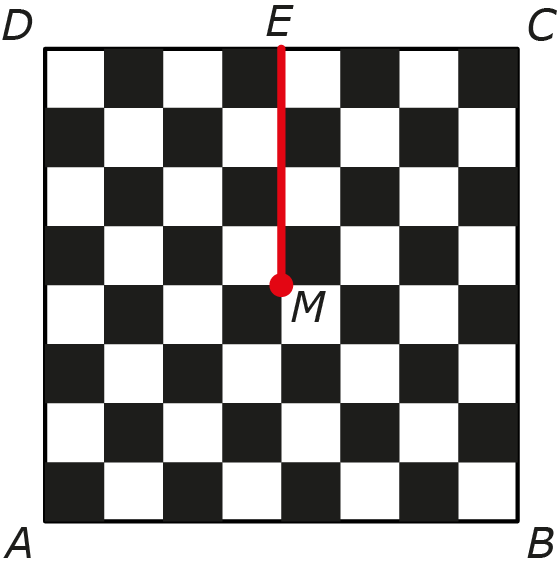
Verbind het midden E van de zijde CD met het midden M van het bord. Knip het bord langs de lijn EM open (de rode lijn in figuur 3).

In plaats van één punt E zijn er dan twee punten E₁ en E₂. Trek dan de twee punten E₁ en E₂ zover uit elkaar dat E₁, M en E₂ op één rechte lijn komen, waarbij het middelpunt M op zijn plaats blijft. Het resultaat is dan als in figuur 4.

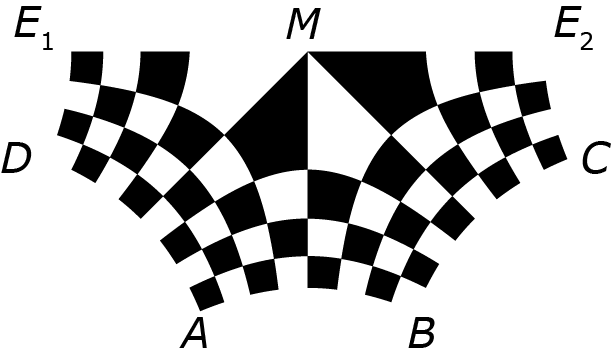
De meeste velden worden richting het oorspronkelijke middelpunt M in elkaar gedrukt. Slechts de vier velden rond het middelpunt M worden uitgerekt en het meest vervormd. Het vervormde bord heeft nog steeds 64 velden, maar geen enkel veld is meer precies vierkant. Veel van de oorspronkelijk rechte randen van de velden zijn een beetje gebogen. Overigens zijn alle hoeken, op die van de vier velden met gemeenschappelijk hoekpunt M na, recht gebleven. Het aantal hoekpunten is nu gelijk aan 85 (81 + 4).

Om het uiteindelijke ontwerp in de figuur aan het begin te krijgen doen we hetzelfde met een tweede schaakbord en draaien we het resultaat over $180^{\circ}$ en plaatsen we  het tegen het eerste vervormde bord. Het resultaat is een vervormd achthoekig schaakbord met 128 velden en 161 hoekpunten (85 + 85 – 9), het ontwerp voor de graantekening van Hans Kuiper.

Schaalvergroting

Als het ontwerp eenmaal geprint is, wordt het zaak daar een enorme schaalvergroting op toe te passen, van papierformaat A3 tot ongeveer twee voetbalvelden groot. Eerst wordt een aantal hoekpunten bepaald van waaruit de rest verder geconstrueerd kan worden. Dat zijn de 41 blauwe stippen in figuur 5.

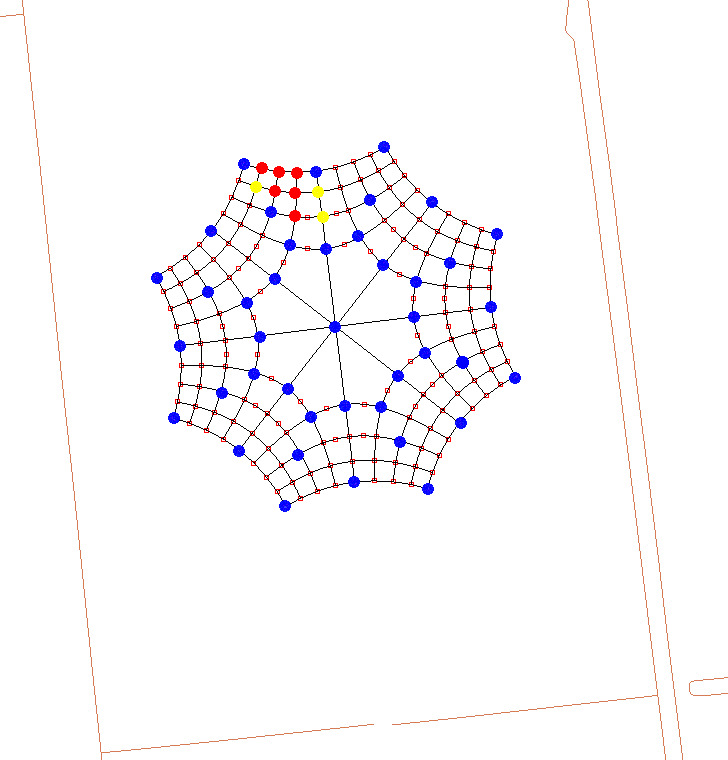
Als die eenmaal in de akker zijn vastgelegd dan zijn de andere 120 hoekpunten van daaruit met bij voorbeeld een meetlint vast te leggen. Om de blauwe stippen in de akker uit te zetten werd een techniek gebruikt die ook in de bouwwereld wordt toegepast om de exacte plaats van heipalen vast te leggen. Met een computer werd het ontwerp op een Google Maps-weergave van de akker geprojecteerd. Zo kon nauwkeurig een plek op de akker worden gekozen. Tegelijk konden de afmetingen zo worden gekozen dat het geheel daarop netjes paste. Toen dat eenmaal naar tevredenheid was, konden van de 41 blauwe stippen uit het ontwerp de GPS-coördinaten worden bepaald. Met een GPS-ontvanger werden die coördinaten vervolgens in het voorjaar voor dat het graan opkwam door een landmeetkundig bureau met paaltjes op de akker gemarkeerd.

Daarna konden de 120 tussenliggende hoekpunten (de rode en gele stippen)  met een meetlint door de kunstenaar zelf worden bepaald en ook met paaltjes gemarkeerd.

Vaak kwam daarbij de hulp van enkele andere deelnemende kunstenaars goed van pas (‘mienskip’).

Maaien is tekenen, oogsten is gummen

Wat je het echte tekenen zou kunnen noemen, kon worden uitgevoerd toen het graan voldoende was opgekomen. Tussen de paaltjes werden markeringstouwen gespannen en in de tussenliggende vlakken werd het graan gemaaid.

Met twaalf vrijwilligers werd die klus in één lange dag van tien uur aanpoten geklaard. Het resultaat was een graantekening die precies past in een cirkel met een middellijn van 142 m, in een vierkant met zijden van 131 m en in een regelmatige achthoek met zijden van 54 m. De totale oppervlakte is 12.300 m² waarvan de helft, 6.150 m², is gemaaid. Helaas was deze graantekening net als de andere zeven geen lang leven beschoren want met de oogst werden ze allemaal als het ware uitgegumd.

Wat resteert zijn luchtfoto's en filmpjes die met drones en vanuit vliegtuigjes zijn gemaakt.

De transformatie

Je zou kunnen denken dat je het schaakbord, na het openknippen, op veel manieren neer zou kunnen leggen, zó dat E₁, M, en E₂ op één lijn komen te liggen, bijvoorbeeld door gewoon alle hoeken te halveren, zo dus:

De titel Conform Schaakbord legt echter wat wiskundige beperkingen op: ‘conform’ betekent dat na de transformatie alle hoeken gelijk gebleven zijn. Dat is in figuur 6 niet gebeurd; alléén hoeken halveren is dus niet conform. De transformatie die we in het begin gezien hebben (figuur 4) is dat wel.

De rechte lijnen zijn ook hier krom getrokken maar de loodrechte stand is overal bewaard gebleven; alleen in het middelpunt M is het misgegaan, daar lijken de hoeken gehalveerd. Dat laatste klopt en in een volgend artikel zullen we zien dat deze transformatie alles te maken heeft met het kwadrateren en worteltrekken van complexe getallen, en die bewerkingen zijn overal conform behalve in de oorsprong.

Dan zullen we ook zien dat wat het plaatje suggereert waar is: de rechte lijnen in het schaakbord zijn allemaal omgebogen tot hyperbolen.

Over Ars et Mathesis

De Stichting Ars et Mathesis wil de belangstelling bevorderen voor kunst die zijn inspiratie vindt in de wiskunde. Ter gelegenheid van haar 7^e lustrum is naast het jaarboek 2018 onder de titel Ode aan M.C. Escher op 't Bildt, Tekeningen in Bildtse graanakkers een extra brochure uitgebracht. Daarin is het volledige project beschreven en worden alle ontwerpen getoond. Deze brochure is te verkrijgen door € 10,- over te maken op bankrekening NL70 ABNA 0552 7118 96 (BIC: ABNANL2A) ten name van Stichting Ars et Mathesis. (Dit is inclusief verzendkosten, voor verzending buiten Nederland komt daar € 5,- extra bij.) Stuur tegelijk ook een e-mail met adresgegevens naar [email protected].