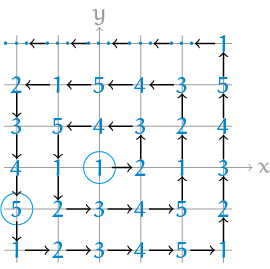
De opgave uit de junior wiskunde olympiade In een assenstelsel worden de roosterpunten via een spiraalvorm tegen de klok in doorlopen. Daarbij wordt op elk roosterpunt een getal uit het rijtje $1, 2, 3, 4, 5$ gezet door in het punt $(0, 0)$ bij $1$ te beginnen en het rijtje eindeloos te herhalen zoals in de figuur hiernaast. De omcirkelde $1$ hoort bij het punt $(0, 0)$ en de omcirkelde $5$ hoort bij het roosterpunt $(-2, -1)$. Welk getal staat op het roosterpunt $(-20, 21)$?

Zoals bij veel mooie opgaven zou je door een oppervlakkige blik op het probleem makkelijk ontmoedigd kunnen raken. Of je de cijfers nu per horizontale, verticale of diagonale rij bekijkt, elke regelmaat lijkt ver te zoeken. Sterker, hoe langer je naar het plaatje kijkt, hoe minder je er wat aan lijkt te hebben. Maar daar zit al een begin van de oplossing: we moeten ons niet te veel laten leiden door de visuele wanorde die is ontstaan door de eendimensionale rij rijtjes $1, 2, 3, 4, 5$ langs een tweedimensionale spiraal over een assenstelsel te verdelen. Om uit te vinden welk cijfer bij welk roosterpunt hoort, doen we precies het omgekeerde: we trekken de tweedimensionale spiraalvorm recht en kijken wat dan de volgorde van de roosterpunten wordt, die nu op een eendimensionale lijn komen te liggen. De kunst is dus het patroon van de spiraal te vertalen in het patroon van de rij rijtjes. We kunnen dat doen door te beschrijven hoe we die spiraal doorlopen, dat wil zeggen: hoeveel stappen doen we steeds naar rechts, boven, links en onder. Het uitrollen komt er dan op neer dat we die aantallen stappen van links naar rechts opschrijven en dus geen onderscheid maken tussen horizontaal of verticaal bewegen. Merk op dat we bij het aantal stappen dat we nodig hebben om in $(-20, 21)$ aan te komen $1$ moeten optellen om het aantal punten te krijgen dat we van $(0, 0)$ tot en met $(-20, 21)$ hebben. De opgave lossen we dan op door dat aantal punten te berekenen en te kijken hoeveel rijtjes $1, 2, 3, 4, 5$ daar in passen: past het precies, dan is het antwoord 5; past het niet, dan is het antwoord $1$, $2$, $3$ of $4$, al naar gelang we nog $1$, $2$, $3$ of $4$ roosterpunten overhebben. 

Van $(0, 0)$ naar $(1, 0)$ gaan we $1$ naar rechts, en van $(1, 0)$ naar $(1, 1)$ dan $1$ omhoog. Daarna gaan we $2$ naar links, naar $(-1, 1)$, en vervolgens $2$ naar beneden, naar $(-1, -1)$. We hebben nu het eerste deel van de spiraalbeweging uitgeschreven,  dat wil zeggen: één keer naar rechts, naar boven, naar links en naar beneden. 

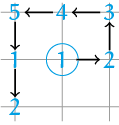
Uitgerold ziet dat er zo uit:

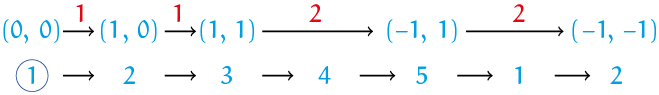
In de volgende draai gaan we $3$ naar rechts, $3$ omhoog, $4$ naar links en $4$ naar beneden. We laten daarbij de rijtjes $1, 2, 3, 4, 5$ weg; het gaat immers alleen maar om het aantal stappen.

En als we er nog een draai aan geven, is het stappenpatroon helemaal duidelijk:

Nu wordt het tijd om te kijken hoeveel stappen we nodig hebben tot we bij $(-20, 21)$ zijn. In de voorbeelden hierboven gingen we steeds tot in een hoekpunt, zoals $(-3, -3)$, dat linksonder in de spiraalvorm ligt. Het punt $(-20, 21)$ ligt echter juist linksboven; om precies te zijn: een punt rechts van $(-21, 21)$. Omdat het (uitgerolde) patroon zo regelmatig is, is het de moeite waard om te kijken hoeveel stappen er nodig zijn om van $(0, 0)$ naar vergelijkbare punten als $(-21, 21)$ te komen, zoals $(-1, 1)$, $(-2, 2)$ en $(-3, 3)$. We vinden daarvoor respectievelijk $4$, $16$ en $36$ stappen: de kwadraten van $2$, $4$ en $6$! Zou dat toeval zijn of zou elk aantal stappen vanuit $(0, 0)$ tot aan een punt linksboven in de spiraalvorm een kwadraat van een even getal zijn? Het antwoord daarop krijgen we vrijwel onmiddellijk als we kijken naar de toenames tussen de kwadraten vanaf $4$:

Het verband met de stappen in de stukjes uitgerolde spiraal die we eerder zagen wordt nog duidelijker als we dit herschrijven tot

en daarna tot

We zien dat het aantal stappen om van $(0, 0)$ naar $(-4, 4)$ te komen $8^2 = 64$ is; het aantal stappen van $(0, 0)$ naar $(-5, 5)$ is $10^2 = 100$. Gaan we door tot $(-21, 21)$, dan vinden we dat we daarvoor $(2 \times 21)^2 = 1764$ stappen nodig hebben. Omdat we van dat aantal $1$ moeten aftrekken om bij $(-20, 21)$ te komen maar ook weer $1$ moeten optellen om het aantal punten te vinden, concluderen we dat het antwoord $1764$ is. Omdat in $1760$ een geheel aantal rijtjes $1, 2, 3, 4, 5$ past, staat op roosterpunt $(-20, 21)$ dus het cijfer $4$. 

Je zou je kunnen afvragen waarom je überhaupt een rijtje als $1, 2, 3, 4, 5$ in een spiraalvorm op de roosterpunten van een assenstelsel zou zetten. Daarop zijn ten minste twee goede antwoorden. Het eerste is: puur voor de lol. Hoewel getallen geen tastbare objecten zijn, kun je er wel mee spelen en plezier hebben in wat er gebeurt als je ermee knutselt, zoals in de varianten op de opgave hieronder. Je ziet dat het rijtje $1, 2$ een heel overzichtelijk schaakbordpatroon geeft, terwijl bij $1, 2, 3, 4$ de regelmaat op de diagonalen opvalt. Aan de andere kant is zo'n soort regelmaat bij een rijtje als $1, 2, 3$ al ver te zoeken, en ook deelbaarheid door twee blijkt geen garantie voor een duidelijk patroon, zoals het rijtje $1, 2, 3, 4, 5, 6$ laat zien.

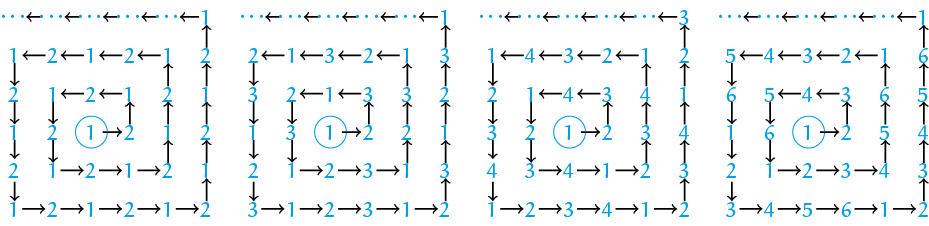
Het tweede antwoord ligt in het verlengde van het vorige: al doende stuit je voor je het weet op verrassende, soms ronduit spectaculaire indrukken, waarvan je zou kunnen proberen te laten zien dat ze meer dan dat zijn, namelijk een wiskundige eigenschap van het geconstrueerde. Voor je het weet, ben je dus met echte wiskunde bezig! De opgave van de JWO is daarvan een mooie illustratie: als je wat langer kijkt naar de wilde verdeling van de cijfers $1$ tot en met $5$ in het assenstelsel, zul je zien dat in de kolom meteen rechts van het startpunt (dus alle punten met $x$-coördinaat $1$) en in de rij meteen boven het startpunt (dus alle punten met $y$-coördinaat $1$) het cijfer $1$ niet voorkomt. Zou dat ook zo zijn als je de spiraal verder volgt, zelfs tot in het oneindige? Om een indruk te geven hebben we hieronder de spiraal wat verlengd; de spiraalpijltjes mag je er zelf bij bedenken. Verdraaid, die enen ontbreken nog steeds waar $x = 1$ of $y = 1$!

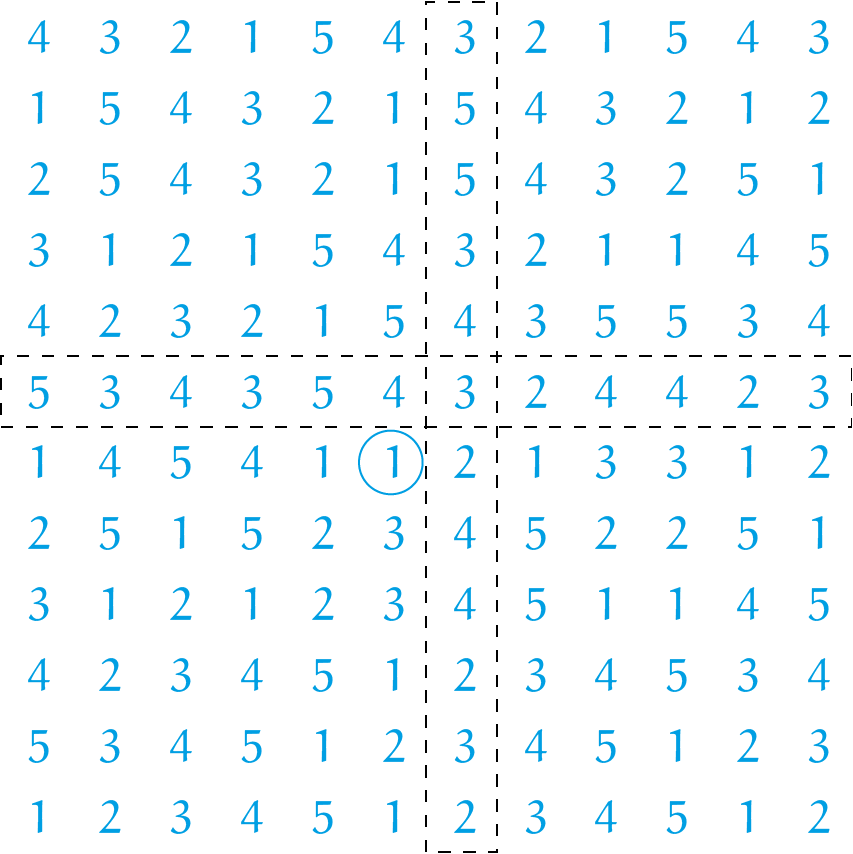
En nu we het er toch over hebben: in het bovenstaande voorbeeld met het rijtje $1, 2, 3, 4, 5, 6$ is dat ook het geval. De conclusie is duidelijk: veel plezier ermee!

Lukt het je te bewijzen dat in spiralen met het rijtje $1, 2, 3, 4, 5$ nooit een $1$ komt te staan in de rij met $y = 1$ of de kolom met $x = 1$, dan kun je je bewijs opsturen naar [email protected]. Onder degenen met een sluitend bewijs worden vijf exemplaren van De dikke Pythagoras verloot.