Een mooie Kangoeroe-opgave van dit jaar was nr. 25 uit de serie wizPROF, bestemd voor havo 4 en 5 en vwo 3, 4, 5 en 6:

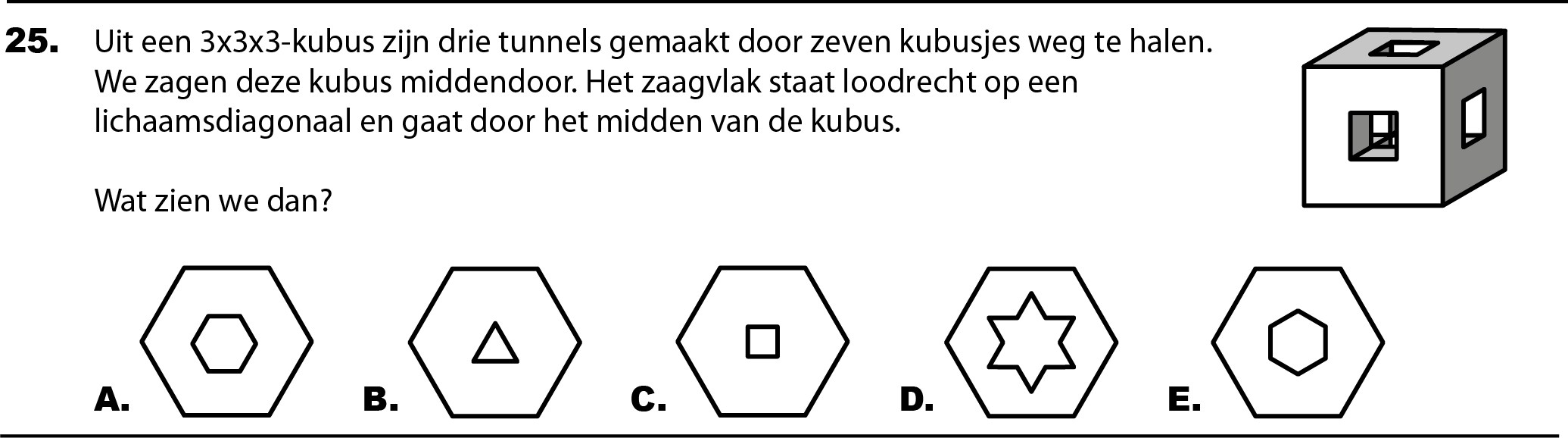
In de Kangoeroe-wedstrijd zijn alle opgaven meerkeuzevragen met vijf alternatieven. Een bewijs of redenering wordt niet gevraagd; alleen het antwoord telt. Je kunt dus met een verstandige gok of met een beetje geluk het goede antwoord raden. Meetkundig inzicht helpt daarbij, maar niet iedereen kan zich ruimtelijke figuren even gemakkelijk voorstellen.

In dit geval kun je het goede antwoord (en nog wat extra's) ook vinden door handig te rekenen met 3D-coördinaten.

Die berekeningen worden eenvoudig als je het 3D-stelsel zo kiest, dat de hoekpunten van de kubus de coördinaten $(\pm 3, \pm 3, \pm 3)$ krijgen.

Als lichaamsdiagonaal kun je nu bijvoorbeeld de lijn door de tegenover elkaar liggende hoekpunten $(-3, -3, -3)$ en $(3, 3, 3)$ nemen.

Het zaagvlak heeft dan als vergelijking $x + y + z = 0$, want dit vlak gaat door de oorsprong en het staat loodrecht op de gekozen lichaamsdiagonaal.

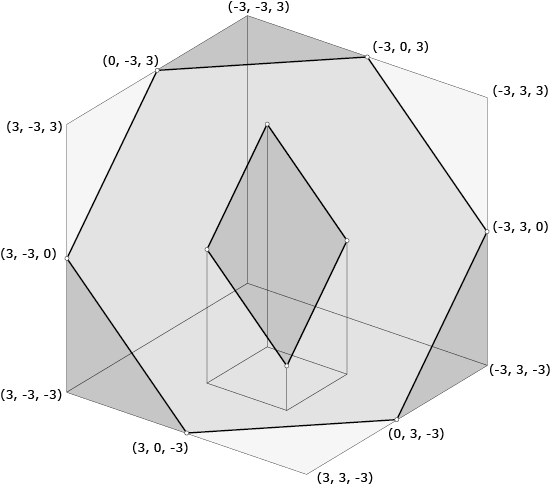
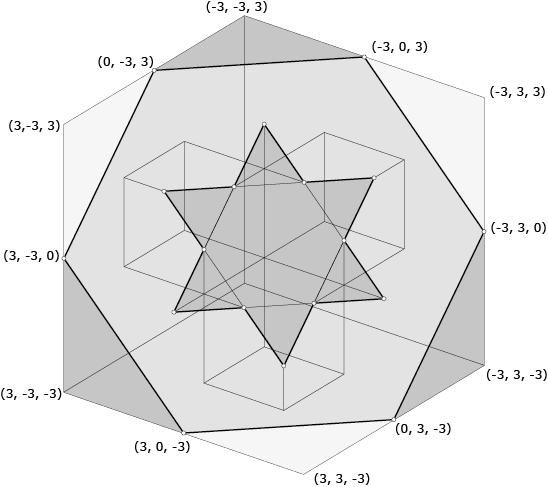
De doorsnede van de kubus met het zaagvlak is de regelmatige zeshoek met hoekpunten $(-3, 0, 3), (-3, 3, 0), (0, 3, -3), (3, 0, -3), (3, -3, 0) \mbox{ en } (0, -3, 3)$ (zie figuur 1). Ook de tunnels en hun doorsnede met het zaagvlak zijn makkelijk in coördinaten uit te drukken. Zo heeft bijvoorbeeld de verticale tunnel als doorsnede met het grondvlak $z = -3$ van de kubus het vierkant met hoekpunten $(\pm1, \pm1, -3)$. De doorsnede van die verticale tunnel met het zaagvlak $x + y + z = 0$ is dus een vierhoek met hoekpunten $(1, 1, -2), (1, -1, 0), (-1, -1, 2) \mbox{ en } (-1, 1, 0)$ want de som van de coördinaten van een punt in het zaagvlak moet nul zijn.

Opgave

Laat door een berekening zien dat die vierhoek een ruit is met hoeken van 60° en 120°.

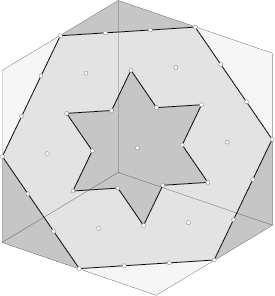
Op dezelfde manier zie je dat de horizontale tunnel die evenwijdig is aan de $x$-as een ruit uit het zaagvlak snijdt met hoekpunten $(-2, 1, 1), (0, 1, -1), (2, -1, -1) \mbox{ en } (0, -1, 1)$. En de tunnel evenwijdig aan de $y$-as snijdt een ruit uit het zaagvlak met hoekpunten $(1, -2, 1), (1, 0, -1), (-1, 2, -1) \mbox{ en } (-1, 0, 1)$. Leg je die drie ruiten over elkaar heen, dan krijg je de oplossing van de opgave: het is een zespuntige ster (een zogenaamde davidsster) met hoeken van 60° in de punten, zie figuur 2.

De hoekpunten van het zaagvlak (de regelmatige zeshoek) en de hoekpunten van de davidsster maken deel uit van de verzameling van alle punten in het vlak $x + y + z = 0$ met gehele coördinaten. Als je die verzameling tekent, krijg je een rooster van gelijkzijdige driehoeken in het zaagvlak (zie figuur 3). Vul nu zelf bij elk punt van het rooster de coördinaten in.

Je ziet dan gemakkelijk dat de oppervlakte van de davidsster precies gelijk is aan het twee-negende deel van de oppervlakte van het zaagvlak!