Figuur 1

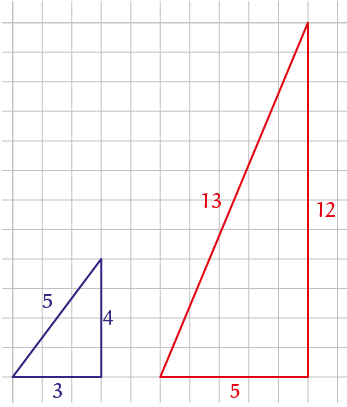
De bekendste daaronder is ongetwijfeld de 3-4-5-driehoek, immers $3^2+ 4^2 = 5^2$. Iets minder bekend is de 5-12-13-driehoek: $5^2 + 12^2 = 13^2 $ (zie figuur 1).

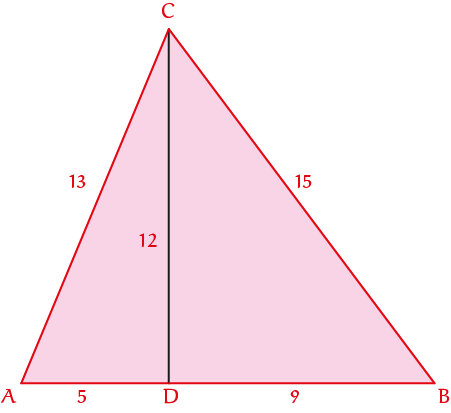
Maak je de 3-4-5-driehoek drie keer zo groot, dan krijg je de 9-12-15-driehoek. Plaats je die tegen de 5-12-13-driehoek, dan ontstaat een driehoek waarvan de lengtes van de zijden opeenvolgende gehele getallen zijn: $13$, $5 + 9 = 14$ en $15$ (zie figuur 2).

Figuur 2

Zou het vaker voorkomen dat een combinatie van twee Pythagoreïsche driehoeken een driehoek oplevert, waarvan de lengtes van de zijden opeenvolgende gehele getallen zijn? Dat is een van de aardige kanten van de wiskunde: je vraagt je niet altijd af of iets nut heeft – overigens blijkt het later vaak toch enig nut te hebben – maar je wilt vaak gewoon weten of iets kan of niet. Met een bewijs dat het niet kan, is het probleem natuurlijk ook opgelost, maar in dit geval hoop je toch minstens nog zo’n driehoek te vinden. We gaan maar eens op onderzoek uit.

Figuur 3

Het onderzoek

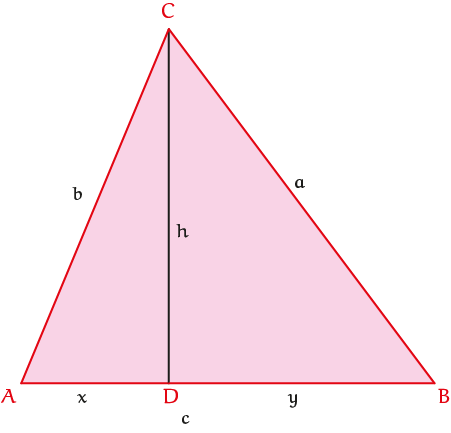
We tekenen in figuur 3 een driehoek $ABC$ en noemen de lengten van de zijden $a$, $b$ en $c$ en de lengte van de hoogtelijn $h$. De hoogtelijn snijdt zijde $AB$ in $D$. De lengte van lijnstuk $AD$ noemen we $x$, die van $BD$ noemen we $y$. Al die lengtes zijn dus gehele getallen.

Omdat $b$, $c$ en $a$ drie opeenvolgende getallen moeten zijn, kiezen we $b= c - 1$ en $a = c + 1$.

Nu is het tijd om je kennis van de algebra te gebruiken, met name van de regel $a^2 - b^2 =(a + b)(a - b)$. De stelling van Pythagoras in $\Delta;ADC$ geeft $b^2 = x^2 + h^2$ en in $\Delta BCD: a^2 = y^2 + h^2$.

Dan is

$$a^2 - b^2 = (y^2 + h^2) - (x^2 + h^2) = y^2 + h^2 - x^2 - h^2 = y^2 - x^2.$$

Dus

$$a^2 - b^2 = y^2 - x^2.$$

Nu is $a^2 - b^2 = (a + b)(a - b)$. Omdat $a = c + 1$ en $b = c - 1$ kun je schrijven: $a + b = (c + 1) + (c - 1) = 2c$ en $a - b =(c + 1) - (c - 1) = 2$.

Dus

$$a^2 - b^2 = 4c.$$

Ook is $y^2 - x^2 = (y - x)(y + x)$. Omdat $y + x = c$ geldt: $y^2 - x^2 = (y - x)(y + x)$ met $y + x = c$.

Dus

$$y^2 - x^2 = (y - x) \cdot c.$$

Combineer je de drie resultaten, dan volgt:

$4c = (y - x) \cdot c$ of, bij deling door $c$:

$ 4 = y - x$ of ook $x = y - 4$ en omdat $y = c - x$ ook $x = c - x - 4$, dus $2x = c - 4$.

We vinden

$$x = \frac12c - 2.$$

Met dit resultaat kun je ook $h$ uitdrukken in $c$: 

In $\Delta ADC$ is $h^2 = b^2 - x^2 = (b + x)(b - x)$.

Omdat $b = c - 1$ en $x = \frac12 c - 2$ volgt:

$b + x = c - 1 + \frac12c - 2 = 1\frac12c - 3 = 1\frac12 (c - 2)$ en $b - x = c - 1 - \frac12 c + 2 = \frac12 (c + 2)$. Dus $h^2 = \frac34(c - 2)(c + 2) = frac34(c^2 - 4)$ of ook: $4h^2 = 3c^2 - 12$.

Omdat $3c^2 - 12$ deelbaar is door $3$, moet $h$ ook deelbaar zijn door $3$. Stel $h = 3n$. Dan volgt $36n^2 = 3c^2 - 12$ of ook $12n^2 = c^2 - 4$ en dus $c^2 = 12n^2 + 4 = 4(3n^2 + 1)$.

Dat betekent dat je $n$ zo moet kiezen dat $4(3n^2 + 1)$ een kwadraat is. Omdat $4$ al een kwadraat is, moet je zorgen dat $3n^2 + 1$ een kwadraat is. Je moet dus positieve gehele getallen $n$ en $t$ vinden, zodat

$$3n^2 + 1 = t^2.$$

Vind je zo’n $n$ en $t$, dan volgt uit het voorgaande: $h = 3n, c^2 = 4t^2$, dus $c = 2t$, $b = 2t - 1$ en $a = 2t + 1$.

Oplossingen

We gaan eerst maar wat proberen:

$n = 1$ geeft $t^2 = 4$, dus $t = 2$: $h = 3$, $c = 4$, $b = 3$ en $a = 5$: de ons bekende 3-4-5-driehoek!

$n = 2$ geeft $t^2 = 13$ en dat is geen kwadraat.
$n = 3$ geeft $t^2 = 28$ en dat is geen kwadraat.
$n = 4$ geeft $t^2 = 49$, dus $t = 7$: $h = 12$, $c = 14$, $b = 13$ en $a = 15$, de driehoek die aanleiding tot ons onderzoek was.

Met een tabel van $3n^2 + 1$ op de rekenmachine vind je ook $n= 15$.

$n = 15$ geeft $t^2 = 676 = 26^2$: $h = 45$, $c = 52, $b= 51$ en $a = 53$.

Met een computerprogramma kun je zoveel waarden vinden als maar wilt. In de tabel staan de eerste acht.

$n$	$ $	$t$	$ $	$h$	$ $	$c$	$ $	$b$	$ $	$a$
$1$		$2$		$3$		$4$
$4$		$7$		$12$		$14$		$13$		$15$
$15$		$26$		$45$		$52$		$51$		$53$
$56$		$97$		$168$		$194$		$193$		$195$
$209$		$362$		$627$		$724$		$723$		$725$
$780$		$1351$		$2340$		$2702$		$2701$		$2703$
$2911$		$5142$		$8733$		$10084$		$10083$		$10085$
$10864$		$18817$		$32592$		$37634$		$37633$		$37635$

Een recursieformule

Het zou mooi zijn als er een regelmaat te vinden is in de rij van $n$: 

$$1, 4, 15, 56, 209, \ldots.$$

Elke volgende $n$ is iets minder dan vier keer de vorige. Wat preciezer: elke $n$ is vier keer de vorige min de voor-vorige! Noem je de getallen $n_1, n_2, n_3, \ldots$, dan geldt $n_k= 4n_{k-1} - n_{k-2}$.

Met die formule vind je volgende getallen heel snel.

Bijvoorbeeld $n_9 = 4 \times 10864 - 2911 = $40545.$ $t^2 = 3 \times 40545^2 + 1 = 4931691076$ en t $= 70226$.

Hiermee is ons probleem opgelost. Er zijn oneindig veel combinaties van twee Pythagoreïsche driehoeken die een driehoek opleveren, waarvan de lengtes van de zijden opeenvolgende gehele getallen zijn. En we hebben zelfs een formule gevonden waarmee we die driehoeken kunnen vinden!

Puntjes op de i

De kritische lezer zal toch een wenkbrauw optrekken bij de afleiding van die recursieformule. Kan dat zomaar: aan de hand van acht voorbeelden concluderen dat de regelmaat altijd geldt? Voor die lezer volgt nog een bewijs, dat de formule juist is. Dan moet je wel even doorbijten!

We zochten oplossingen voor de vergelijking $3n^2 + 1 = t^2$ of ook $t^2 - 3n^2 = 1$.

Die vergelijking kun je ook schrijven als $(t - n\sqrt 3)(t + n\sqrt 3) = 1$.

Vul je de eerste oplossing $n = 1$ en $t = 2$ in, dan staat er $(2 - \sqrt3)(2 + \sqrt3) = 1$.

Kwadrateren levert: $(2 - \sqrt 3)^2(2 + \sqrt 3)^2 = 1$.

Gebruik van de regel $(a$ ± $b)^2 = a^2 \pm 2ab + b^2$ geeft $(2 - \sqrt 3)^2 = 4 - 4\sqrt 3 + 3 = 7 - 4\sqrt 3$ en $(2 + \sqrt 3)^2 = 4 + 4\sqrt 3 + 3 = 7 + 4\sqrt 3$.

Dus $(2 - \sqrt 3)^2(2 + \sqrt 3)^2 =(7 - 4\sqrt 3)(7 + 4\sqrt 3) = 1$.

En $(7 - 4\sqrt 3)(7 + 4\sqrt 3) = 72 - 42 \cdot 3 = 1$.
Dat betekent dat ook $n= 4$, $t = 7$ een oplossing is.

De volgende oplossing vind je door $(2-\sqrt 3)^3(2 + \sqrt 3)^3 = 1$ uit te werken. En eigenlijk hoef je alleen maar $(2 + \sqrt 3)^3 = (2 + \sqrt 3)(2 + \sqrt 3)^2$ uit te werken:

$(2 + \sqrt 3)^3 = (2 + \sqrt 3)(7 + 4\sqrt 3) =14 + 8\sqrt 3 + 7\sqrt 3 + 12 = 26 + 15\sqrt 3$.

Dus $n = 15$ en $t= 26$ is een oplossing.

Er is bewezen (dàt bewijs voert hier te ver) dat alle oplossingen van de vorm $t+ n\sqrt 3 = (2 + \sqrt 3)^p$ zijn met $p$ geheel en positief.

We tonen nu aan dat $(2 + \sqrt 3)^k = 4 \cdot (2 + \sqrt 3)^{k-1} - (2 + \sqrt 3)^{k-2}$. Delen door $(2 + \sqrt 3)^{k-2}$ geeft $(2 + \sqrt 3)^2 = 4 \cdot (2 + \sqrt 3) - 1$ of ook $7 + 4\sqrt 3 = 8 + 4\sqrt 3 - 1$ en dat klopt!

Wiskundige achtergrond

Een vergelijking van het type $x^2 - ky^2 = 1$ met $k$, $x$ en $y$ gehele getallen heet, hoewel al bij Diophantus bekend, een vergelijking van Pell, genoemd naar de Engelse wiskundige John Pell (1611 - 1685). Zulke vergelijkingen zijn in de loop van de tijd uitvoerig bestudeerd en opgelost. In Pythagoras 57-4, april 2018, werd deze gebruikt bij de runderen van de zonnegod. Ze hebben oneindig veel oplossingen, die je allemaal kunt vinden als je eenmaal één oplossing hebt gevonden. Dat vinden van die eerste oplossing is de crux, in ons geval gelukkig tamelijk eenvoudig. Maar in het geval van $k = 61$ bijvoorbeeld is de kleinste oplossing: $x = 1766319049$ en $y = 226153980$ en die vind je niet met wat puzzelen! De Indiase wiskundige Bhaskara (1114 - 1185) vond al een algoritme om een eerste oplossing te vinden. Tegenwoordig gebeurt dat met behulp van kettingbreuken.