De profielwerkstukwedstrijd van 2025 kende acht inzendingen met opnieuw een grote variatie aan onderwerpen. Dit jaar werden de stukken beoordeeld door Maarten de Boeck, Enno Diekema, K.P. Hart, Niels Kolenbrander en Lars Pos. 

Polina Zemskova schreef over een SIR-model waarmee het aantal geïnfecteerden en gezonde mensen tijdens de coronapandemie kon worden gemodelleerd. Ze liet zien hoe de modelparameters op basis van echte data gekozen kunnen worden. Boas Bakker ontwikkelde een indrukwekkend interactief programma waarmee leerlingen bij het vak Scheikunde namen voor moleculen kunnen leren. Zijn programma maakt het mogelijk om vrijwel elk molecuul in 3D weer te geven. Monica Stolk verdiepte zich in de geschiedenis van het oplossen van derdegraadsvergelijkingen en besprak daarbij ook enkele alternatieve oplossingsmethoden. Beatriz Abelha en Liara de Groot gaven een uitgebreide uiteenzetting over de rol van wiskunde in de architectuur, en maakten op basis daarvan een maquette. Een abstractere bijdrage kwam van Bram Leisink en Johnathan Yazvin, die onderzoek deden naar hoger-dimensionale polytopen en hoe deze kunnen worden uitgeklapt naar lagere dimensies – nuttig wanneer men een object uit de vierde dimensie wil visualiseren op een tweedimensionaal vlak.

Na uitvoerig beraad koos de jury drie profielwerkstukken die zich duidelijk onderscheidden van de rest. Het eerste betrof het project Crazy Chroma Challenge van Elise van der Sanden en Janneke Bax. In hun werk voegden zij een nieuw familielid toe aan de bekende Rubik-familie. De vorm – een icosaëder – bestond al, maar de door hen bedachte kleurverdeling maakte het tot een geheel nieuwe puzzel. Ze beschreven hoe ze met behulp van wiskunde en een 3D-printer de puzzel ontwierpen en vervaardigden. Voor deze nieuwe Rubik puzzel berekenden ze ook het aantal mogelijke configuraties, namelijk $23\,563\,902\,142\,421\,896\,679\,424\,000$ mogelijkheden. Daarnaast vonden ze een oplosstrategie voor deze puzzel en die hebben ze toegelicht met video's. Al met al een zeer indrukwekkende en creatieve bijdrage.

Het tweede project was van Femke Maat, die een uitbreiding op het kaartspel SET ontwierp. In het originele spel moeten vier kaarten worden gevonden die voor elk van vier eigenschappen óf helemaal gelijk, óf helemaal verschillend zijn. Waar het standaardspel drie keuzes per eigenschap kent, onderzocht Femke een variant met vier keuzes. Ze gaf direct aan dat het spel daarmee minder speelbaar werd, maar toonde aan dat het interessante wiskundige vragen opleverde. Ze bepaalde onder andere dat er $25\,600$ mogelijke sets bestaan in deze nieuwe variant en leidde zelfs een algemene formule af voor het aantal mogelijke sets bij $p$ keuzes per aspect:

$$\frac{(p + p!)^4 - p^4}{p!}.$$

Een indrukwekkend stuk wiskundig redeneren.

Het derde geselecteerde profielwerkstuk was van Tobias Crommelin en Dylan Spence, die een navigatiesysteem ontwierpen voor hun school. Ze modelleerden de school als een graaf met knopen en verbindingen, waarbij voor elke verbinding een gewicht werd toegekend, bijvoorbeeld op basis van afstand. Vervolgens gebruikten ze Dijkstra’s algoritme om optimale routes te vinden. later maken ze het model complexer en hielden ze rekening met piekuren waarin gangen drukker zijn en routes langzamer verlopen. Dit maakt de gewichten dynamisch. Door deze dynamische gewichten konden zij de doorstroming realistisch modelleren. Hun systeem werd bovendien geijkt aan de hand van concrete metingen binnen de school.

Deze drie profielwerkstukken vielen dusdanig op dat hun makers werden uitgenodigd om hun onderzoek te presenteren op het Nederlands Mathematisch Congres.

De presentaties

Op 23 april tijdens het Nederlands Mathematisch Congres presenteerden Elise en Janneke, Femke, en Dylan en Tobias hun werk in de strijd om de titel ‘Beste Wiskundige Profielwerkstuk van 2025’.

Elise en Janneke trapten af met De Creatie van de Crazy Chroma Challenge (kortweg C³). Ze begonnen met de uitleg van het ontwerp en hadden hun zelfbedachte puzzel fysiek meegenomen, tot groot enthousiasme van het publiek. Hoewel de puzzel wat wiebelig was, zag deze er visueel aantrekkelijk uit. De jury prees hun creativiteit en het originele idee. Daarna bespraken ze op heldere wijze de combinatoriek achter de puzzel en presenteerden ze een algoritme voor het oplossen ervan. Wel merkte de jury op dat de duidelijke instructievideo’s die bij hun profielwerkstuk hoorden, tijdens de presentatie ontbraken.

Vervolgens presenteerde Femke haar uitgebreide variant op SET. Ze was eerlijk over het feit dat het spel door haar uitbreiding moeilijk speelbaar werd, maar legde overtuigend uit hoe dit juist leidde tot interessante wiskundige vraagstukken. Hoewel ze niet al haar onderzoeksvragen volledig wist op te lossen – iets wat haar zeker niet kwalijk werd genomen, gezien de complexiteit – formuleerde ze aan het eind van haar presentatie twee sterke onderzoeksvragen: hoeveel kaarten kunnen worden neergelegd zonder dat er een set ontstaat, en wat is het maximale aantal sets bij een gegeven aantal kaarten? Om in je eentje je tanden te zetten in zulke vragen, vond de jury indrukwekkend.

Dylan en Tobias sloten af met hun presentatie van Nooit meer een briefje halen, over het navigatiesysteem binnen hun school. Hun opbouw was helder en stapsgewijs: van grafentheorie en Dijkstra’s algoritme tot aan de toepassing van verkeerstheorie en dynamische modellen op de eigen schoolomgeving. Hun programma hield rekening met praktische factoren zoals drukte en obstakels in gangen, en werd getoetst aan de hand van echte metingen. Hoewel de interface volgens de jury nog gebruiksvriendelijker zou kunnen, was het geheel technisch zeer knap uitgevoerd. Het publiek was enthousiast en stelde veel vragen over mogelijke uitbreidingen en toepassingen.

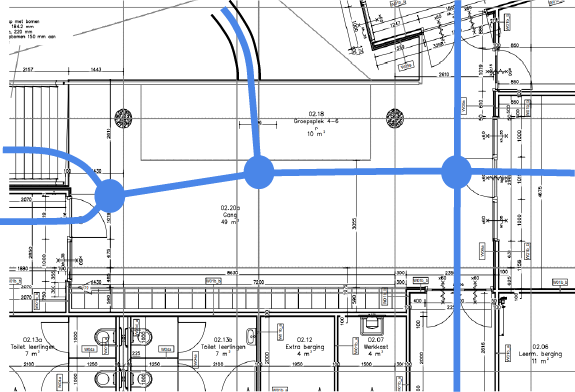
Na alle presentaties maakte de jury de winnaars bekend. Dylan en Tobias mochten met de eerste prijs naar huis, vanwege de knappe combinatie van wiskunde, informatica en veldwerk in een toepasbare oplossing. Femke eindigde op de tweede plaats, dankzij de theoretische diepgang van haar onderzoeksvragen. Janneke en Elise behaalden een verdiende derde plaats met hun originele puzzelontwerp en creatieve aanpak.