
Wat is de kans op een stompe driehoek
Stel dat je een driehoek $ABC$ hebt. Neem aan dat $AB$ de langste zijde is. Kun je dan uitrekenen wat de kans is dat de hoek bij $C$ stomp is?
Als je denkt dat het antwoord op bovenstaande vraag 'ja' is en al een idee voor een aanpak hebt, raden we je aan om vooral eerst die aanpak te proberen en dan alsnog dit artikel helemaal te lezen. Als je nog geen idee hebt hoe je deze kansberekeningsvraag kunt beantwoorden, dan kunnen de ideeën en vragen hieronder je op weg helpen.
We gebruiken de standaardnotatie voor de zijden van de driehoek: $a$ is de overstaande zijde van hoek $A$, $b$ en $c$ zijn de overstaande zijden van $B$ en $C$. Merk allereerst op dat de langste zijde in een driehoek correspondeert met de grootste tegenoverliggende hoek. De kans dat de hoek bij $C$ stomp is, is dus meteen de kans op een stompe driehoek $ABC$ vanwege de aanname dat $c$ de langste zijde is. In het vervolg nemen we voor het gemak $c = 1$.
Een rechthoekige driehoek is een grensgeval tussen driehoeken met alleen scherpe hoeken en driehoeken met een stompe hoek. In de gegeven driehoek heeft de langste zijde lengte $1$, dus als het een rechthoekige driehoek is zou deze zijde de hypotenusa moeten zijn. De andere twee zijden hebben dan dus lengten $a$ en $b$, met $0 < a$, $b < 1$.
Opgave 1Waaraan moet $a + b$ voldoen opdat de zijden met lengten $a$, $b$ en $c = 1$ daadwerkelijk een driehoek vormen? |
Opgave 2Stel, gebruikmakend van de stelling van Pythagoras of van de cosinusregel, een ongelijkheid op voor $a^2 + b^2$, waaraan moet worden voldaan om een stompe driehoek te verkrijgen. |
Met behulp van oppervlaktes kunnen we de volgende vraag beantwoorden: "Stel $0 < a$, $b < 1$. Wat is de kans dat $a^2 + b^2 < 1$, gegeven dat $a + b > 1$?"

Deze kans kun je uitrekenen met behulp van oppervlaktes. Als voorbeeld voor deze aanpak nemen we een simpel dartbord; zie figuur 1. Het hele dartbord heeft een oppervlakte van $20^2\pi\ cm^2$, en het middelste deel heeft een oppervlakte van $5^2\pi\ cm^2$. Als iemand niet goed kan mikken, dan kun je aannemen dat de kans om het pijltje in een willekeurig gebiedje van $1\ cm^2$ te gooien even groot is voor een gebiedje in het midden als voor een gebiedje elders op het bord. Als dat zo is, is de verhouding tussen de oppervlakte van het midden en de totale oppervlakte bepalend voor de kans om het midden te raken: de kans dat je het midden raakt, gegeven dat je het bord raakt, is
$$\frac{opp.midden}{opp.totaal} = \frac{25\pi}{400\pi} = \frac{1}{6}.$$
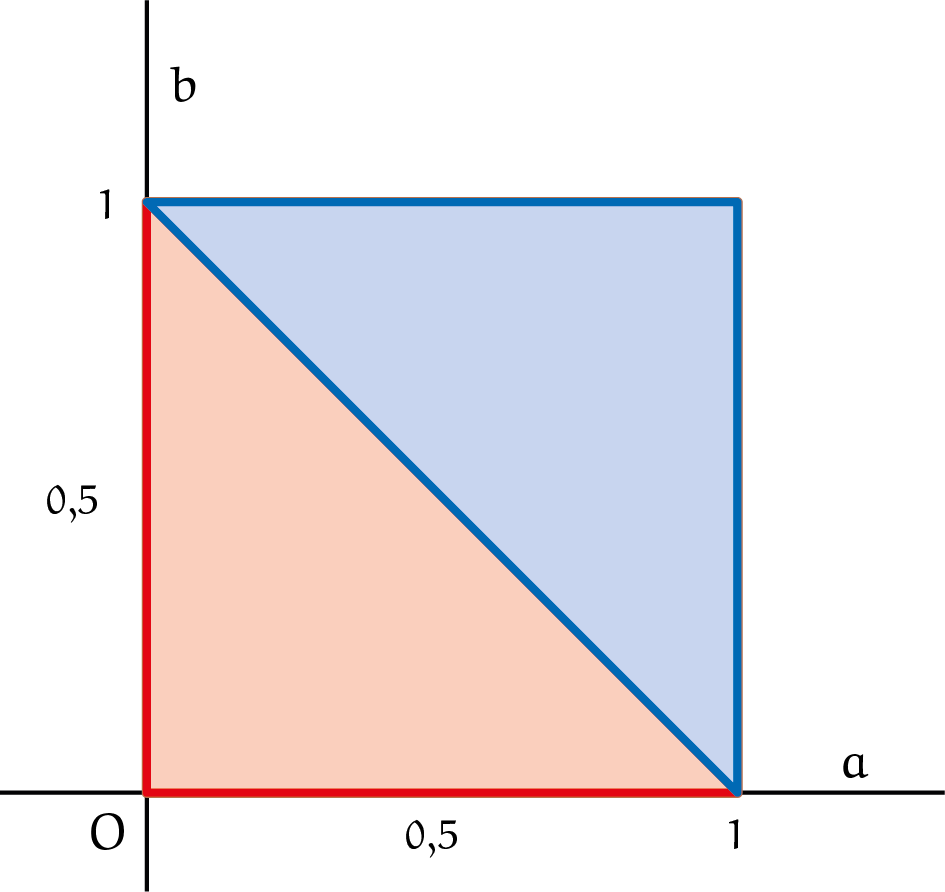
Analoog hieraan kun je met de tekening in figuur 2 snel inzien dat voor $0 < a, b < 1$, de kans op $a + b > 1$ gelijk is aan $0{,}5$: de blauwe driehoek is het gebied waar geldt dat $a + b > 1$.
Opgave 3Teken binnen het vierkant in figuur 2 ook het gebied waarin $a^2 + b^2 < 1$. (Noot: het gebied $a^2 + b^2 < 1$ is het gebied binnen een cirkel met straal $1$ en centrum $O$ in het $a,b$-vlak.) Wat is de oppervlakte? |
Opgave 4Bepaal met behulp van figuur 2 en het antwoord op opgave 3 de oppervlakte van het gebied waarvoor geldt $a^2 + b^2 < 1$ en $a + b > 1$ en leid daaruit af dat de kans op een stompe driehoek gelijk is aan $$\frac{opp.overlap}{opp.driehoek}=\frac{\pi}{2}-1\approx 0{,}571.$$ |
Het antwoord op de vraag uit de inleiding lijkt daarmee 'ja': we kunnen de kans berekenen en hij is gelijk aan $\frac{\pi}{2}- 1$. Er zit echter een addertje onder het gras. Laten we dezelfde vraag eens op een meetkundige manier benaderen.
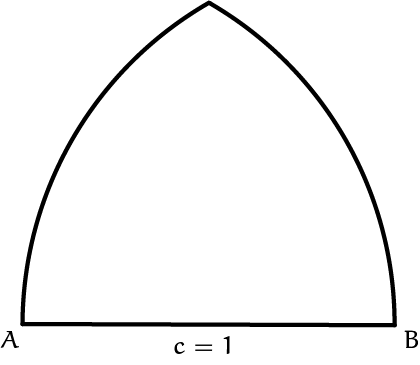
Teken een lijnstuk $AB$ met lengte $1$ en teken vervolgens het gebied waarbinnen hoek $C$ moet liggen opdat $AB$ de langste zijde van de driehoek is. De vraag is nu: "Als we $C$ hier willekeurig kiezen, wat is dan de kans dat driehoek $ABC$ een stompe hoek heeft?"
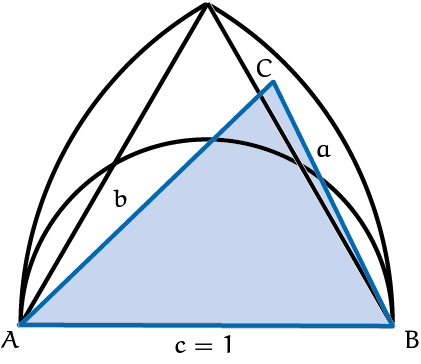
AC = b < 1 en BC = a < 1
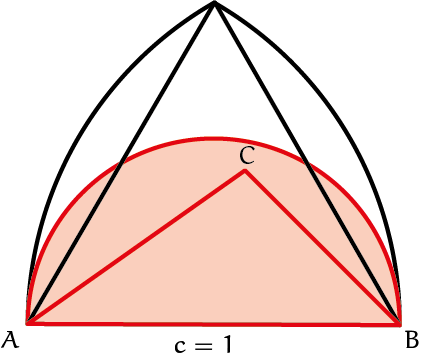
In figuur 3a zie je het gebied waarbinnen hoekpunt $C$ moet liggen om aan de eis $0 < a, b < 1$ te voldoen. Het wordt begrensd door twee cirkelbogen met straal 1. Vervolgens kun je de Stelling van Thales toepassen: een driehoek met basis $c$ en hoekpunt $C$ op de halve cirkelboog in figuur 3b en figuur 3c is een rechthoekige driehoek. Dus iedere driehoek met basis $c = 1$ en hoekpunt $C$ binnen de halve cirkel heeft een stompe hoek $C$. We kunnen nu weer oppervlaktes gebruiken om de kans op een stompe driehoek te berekenen.
Opgave 5Bepaal de oppervlakte van de gehele afbeelding in figuur 3a. Deze oppervlakte representeert alle mogelijkheden om een driehoek te maken die voldoet aan de voorwaarden. |
Opgave 6Wat is de oppervlakte van de (rode) halve cirkel in figuur 3c? Deze stelt alle manieren voor waarop de gevormde driehoek een stompe driehoek is. |
Op basis van de antwoorden op opgave 5 en 6 kun je de volgende conclusie trekken: de kans op een stompe driehoek is
$$\frac{\frac{\pi}{8}}{2\cdot\frac{\pi}{6} - \frac{1}{2}\cdot\frac{\sqrt{3}}{2}} = \frac{3\pi}{8\pi-6\sqrt{3}}\approx 0{,}639.$$
Wat is hier aan de hand? Het addertje onder het gras is de aanname die we maakten bij het dartbord: de kans om een willekeurig gebiedje van $1\ cm^2$ te raken is overal even groot. Dit heet een uniforme kansverdeling. Impliciet hebben we voor beide bovenstaande berekeningen diezelfde aanname gemaakt, namelijk dat de kansverdeling voor een punt $(a, b)$ of voor de hoek $C$ uniform is. Dit heet ook wel het Principle of Indifference: als je geen goede reden hebt waarom de kansen niet overal gelijk zouden zijn, neem je maar aan dat dat wel zo is. Dit gaat vaak goed, maar zoals je ziet kan het ook tot paradoxale conclusies leiden.
