AchterOPgave 62-5
[ooO]
De wiskundige V.I. Arnold (1937 – 2010) heeft een boekje samengesteld met denkoefeningen en wiskundeopgaven 'voor kinderen van 5 tot 15'. Ze hebben uiteenlopende onderwerpen en moeilijkheidsgraden. De meeste ervan doen meer een beroep op goed nadenken dan op hogere wiskunde. In deze jaargang van Pythagoras plaatsen we achterop telkens één van deze opgaven.
Opgave 60
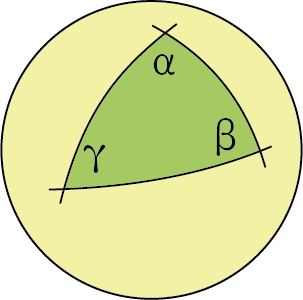
Bepaal de oppervlakte $S$ van een driehoek met hoeken $\alpha$, $\beta$, $\gamma$ op een bol met straal $1$, waarvan de zijden liggen op grootcirkels (doorsnedes van de bol met platte vlakken die door het middelpunt van de bol gaan: de evenaar en de meridianen zijn bijvoorbeeld wél grootcirkels, maar de poolcirkels niet).
Toon aan dat deze oppervlakte gelijk is aan $\alpha + \beta + \gamma - \pi$ (bijvoorbeeld voor een driehoek met drie rechte hoeken bedraagt $S = \pi/2$, een achtste van de oppervlakte van de bol).