
AchterOPgave 62-6
De wiskundige V.I. Arnold (1937 – 2010) heeft een boekje samengesteld met denkoefeningen en wiskundeopgaven 'voor kinderen van 5 tot 15'. Ze hebben uiteenlopende onderwerpen en moeilijkheidsgraden. De meeste ervan doen meer een beroep op goed nadenken dan op hogere wiskunde. In deze jaargang van Pythagoras plaatsen we achterop telkens één van deze opgaven.
[ooO]
Opgave 31bis
Construeer de doorsnede van een kubus en een plat vlak dat door drie gegeven punten op de ribben van de kubus gaat.
[Teken de veelhoek die de doorsnede vormt van het vlak en de zijden van de kubus.]
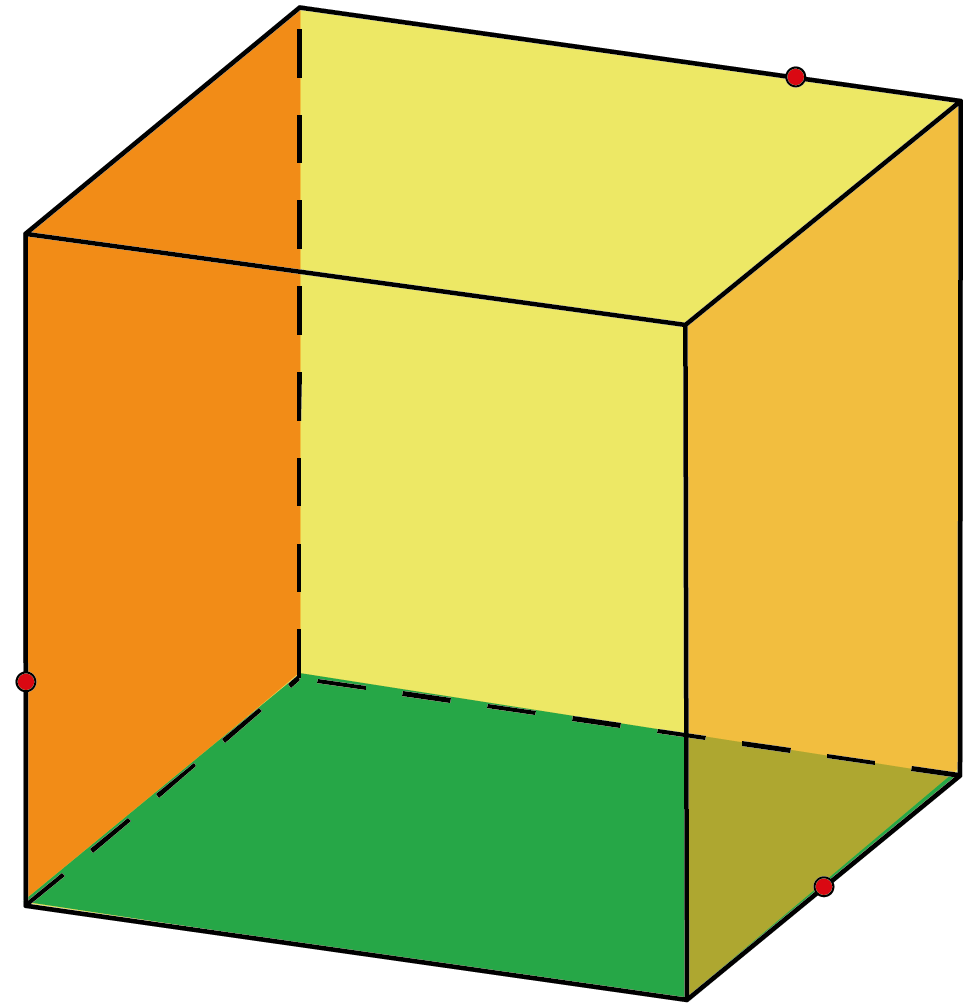
Als je verder doorscrolt kun je een hint vinden. De oplossing staat bij [Bekijk oplossing].
(nog ietsje verder voor de hint)
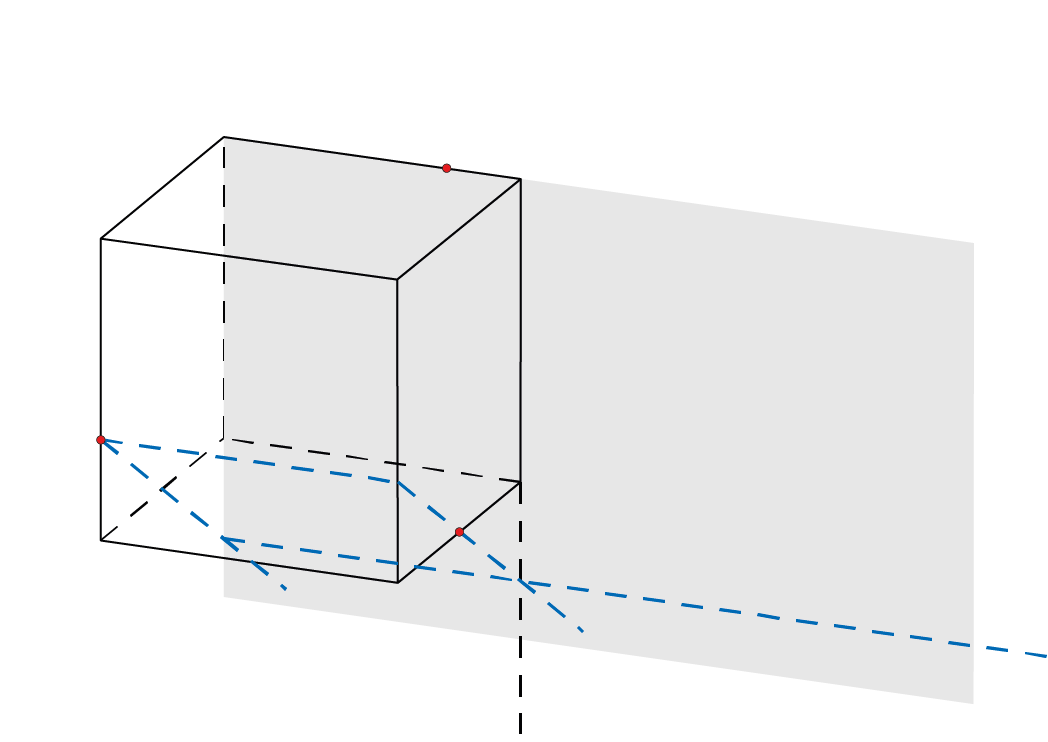
De gevraagde doorsnede heeft als hoekpunten de drie gegeven punten en verder de snijpunten van het vlak door die drie punten met andere ribben van de kubus. De lijn door twee van de gegeven punten snijdt elk van beide vlakken waar het derde punt op ligt (d.w.z. de vlakken waar de twee zijvlakken van de kubus waar het derde punt toe behoort in liggen). Probeer zo’n snijpunt te bepalen; gebruik de hulplijnen en het grijze vlak. Met dat snijpunt vind je dan een punt op een ribbe van de kubus, een hoekpunt van de doorsnede. Verder kun je gebruiken dat de zijden van de doorsnede op tegenover elkaar gelegen zijvlakken van de kubus evenwijdig zijn.
Bij [Bekijk oplossing] kun je de oplossing vinden.
Bekijk oplossing
