Eerst nogmaals de hint:

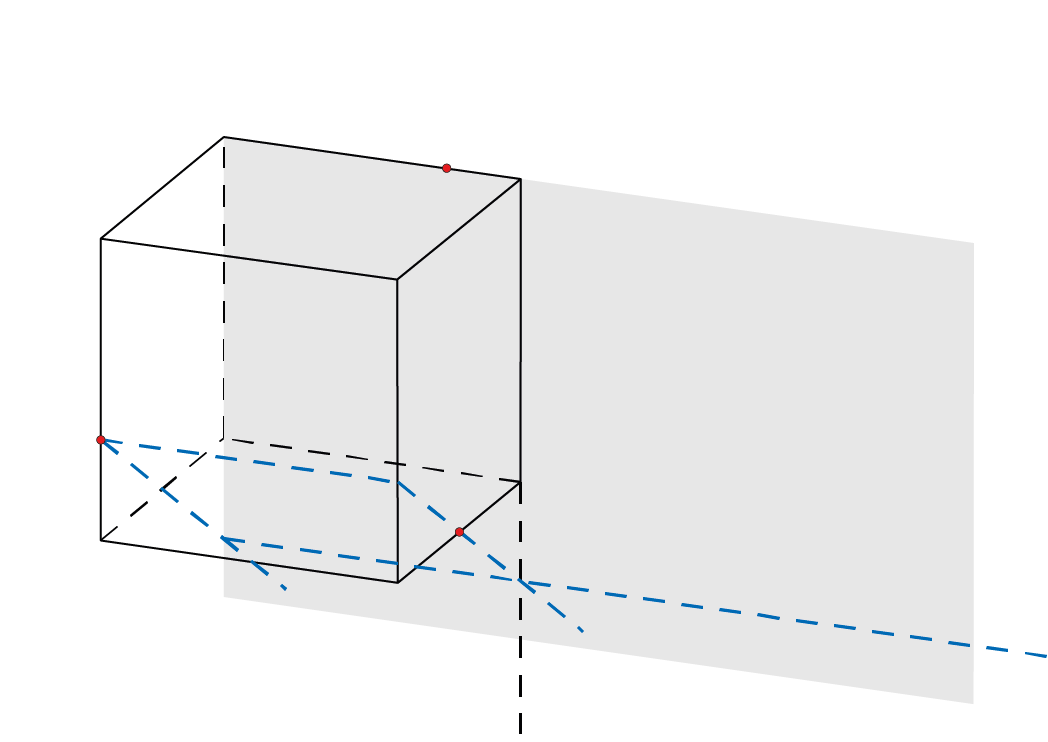
De gevraagde doorsnede heeft als hoekpunten de drie gegeven punten en verder de snijpunten van het vlak door die drie punten met andere ribben van de kubus. De lijn door twee van de gegeven punten snijdt elk van beide vlakken waar het derde punt op ligt (d.w.z. de vlakken waar de twee zijvlakken van de kubus waar het derde punt toe behoort in liggen). Probeer zo’n snijpunt te bepalen; gebruik de hulplijnen en het grijze vlak. Met dat snijpunt vind je dan een punt op een ribbe van de kubus, een hoekpunt van de doorsnede. Verder kun je gebruiken dat de zijden van de doorsnede op tegenover elkaar gelegen zijvlakken van de kubus evenwijdig zijn.

 

En als je doorscrolt vind je de oplossing, waarbij de hint iets verder uitgewerkt is om te komen tot de eerste van de drie overgebleven hoekpunten van het snijvlak.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

(nog een klein stukje doorscrollen)

 

 

 

 

 

 

 

 

 

 

 

 

 

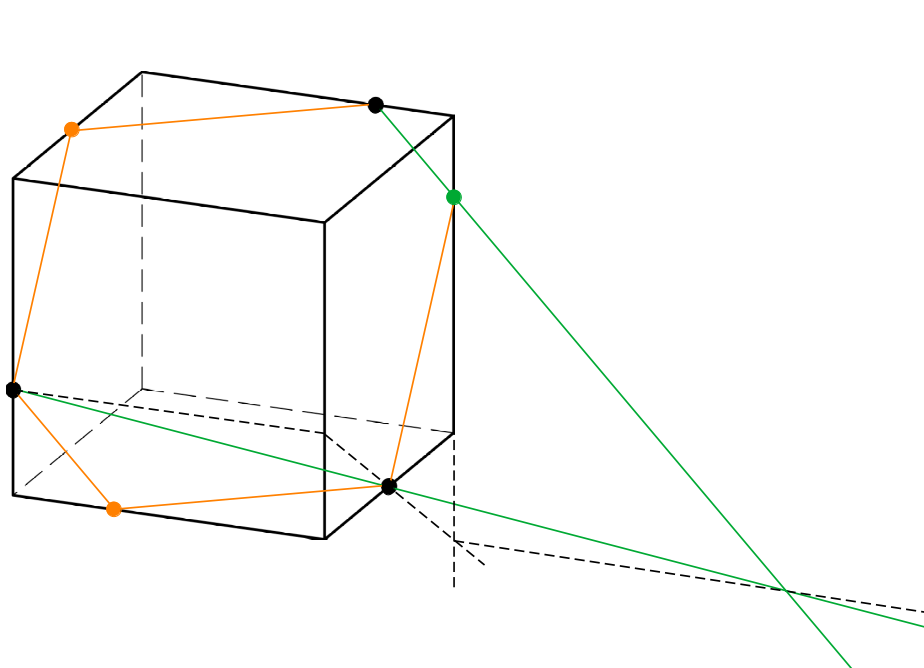
De doorsnede is een (onregelmatige) zeshoek, waarvan de drie gegeven punten hoekpunten zijn en waarvan tegenoverliggende zijden evenwijdig zijn. De figuur toont een ‘constructie zonder woorden’ om eerst één van de drie onbekende hoekpunten te bepalen en daarna de andere twee.