Opgave 1

Driehoek $N_2 SV$ is een gelijkbenige driehoek. $\angle VN_2 S= \alpha$, dus $\angle N_2 VS= \angle N_2 SV=90-\alpha/2$. $\angle VSR=\angle N_2 SV+\angle N_2 SR=90^o$.

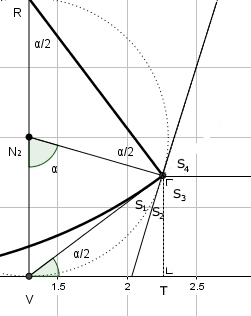Opgave 2

Bekijk de afbeelding hiernaast (een deel van figuur 3 uit het artikel) en de getekende hulplijn SW, die raakt aan de cirkel. Vierhoek $VWSN_2$ heeft twee hoeken van $90^o$. Dus $\angle W=180^o -\alpha$. Omdat $EF$ in figuur 4 evenwijdig is aan $SW$, geldt: $\angle E_1 =\alpha$.

Opgave 3

In figuur 4 is de binnenhoek bij $E$ gelijk aan $180^o-\alpha$. En dus maakt verplaatsing $SF$ een hoek $\alpha/2$ met de horizontaal. Maar $VS$ in figuur 2 maakt ook een hoek van $\alpha/2$ met de horizontaal. De lijnen zijn evenwijdig en dus is $VS$ de raaklijn aan de cycloïde.