
De Cycloïde: de Huygensslinger
In de vorige twee delen over de cycloïde bespraken we de eigenschappen van deze bijzondere kromme. In deel I zagen we de cycloïde als de brachistochroon (of de kromme van de kortste tijd): de snelste manier om een kraal naar beneden te laten glijden, is via de baan van een cycloïde. In deel II ontdekten we dat de cycloïde tautochroon (ook wel isochroon) is: die kraal heeft altijd dezelfde tijd nodig om in het laagste punt aan te komen, ongeacht op welke hoogte hij start.
In deel III bekijken we een toepassing van deze laatste eigenschap. Zo’n 350 jaar geleden ontwikkelde Christiaan Huygens een slinger die altijd dezelfde periode had ongeacht de grootte van de slingerbeweging. Een belangrijke ontwikkeling, want daarmee kon voor het eerst een betrouwbare klok gemaakt geworden.

De Huygensslinger
De grote Nederlandse wis- en natuurkundige en astronoom Christiaan Huygens (1629-1695) probeerde een slingeruurwerk te maken waarbij de slinger isochroon was, d.w.z. onafhankelijk van de uitwijking altijd dezelfde slingertijd had. Bij een gewone slinger is voor kleine uitwijkingen wel sprake van een constante slingertijd maar bij grotere uitwijkingen neemt de slingertijd toe. De slingertijd $T$ bij kleine uitwijkingen wordt gegeven door de benaderingsformule: $T=\sqrt{l/g}$, waarin $l$ de lengte is en $g$ de versnelling van de zwaartekracht.
Met de kennis die we hebben opgedaan in het vorige artikel (Deel II “De cycloïde als tautochroon of isochroon”, Pythagoras 57-2, november 2017) weten we dat de massa aan het einde van zijn slinger volgens een cycloïde zou moeten bewegen. Maar bij een ‘gewone’ slinger zal het uiteinde altijd een deel van een cirkelbaan beschrijven. Om bij grotere uitwijkingen dezelfde slingertijd te houden moest Huygens dus de lengte iets kleiner laten worden, zodat het uiteinde van de slinger een cycloïde beschrijft. Huygens slaagde daarin door bij het ophangpunt twee gebogen metalen plaatjes te plaatsen, de zogenaamde ‘wangen’. De Huygensslinger bewoog bij het ophangpunt langs de wangen waardoor de effectieve lengte van de slinger korter werd. De vorm van die wangen? Huygens ontdekte dat elk van de wangen ook een cycloïde moet zijn, en wel precies dezelfde cycloïde als die welke de massa beneden volgt. In figuur 2 zie je de tekening van Huygens zelf.
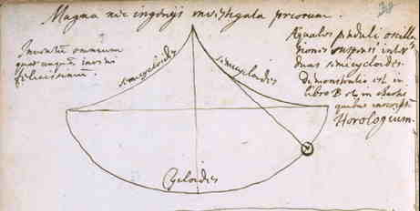
met twee cycloïden
Het ontwerp
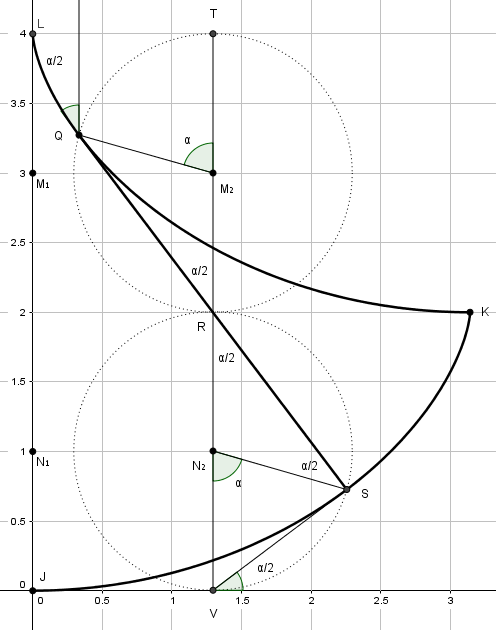
Om er goed aan te kunnen rekenen, bekijken we figuur 3. Uiteraard is de slingerbeweging symmetrisch, maar we bekijken even alleen het deel van de slinger dat naar rechts beweegt. In de figuur zien we twee identieke cycloïden: van $L$ naar $K$ en van $J$ naar $K$. Het ‘wangetje’ van Huygens is alleen maar het bovenste stuk bij $L$. De slingermassa beweegt van $J$ richting $K$. De massa keert ergens om en passeert $J$ naar links. Zo ontstaat een isochrone slinger. De draad waaraan de massa vastzit, loopt van $L$ langs het wangetje tot $Q$ en vandaar in een rechte lijn naar $S$.
De slingerlengte is $4$ in de tekening (willekeurig gekozen). Wat we nu moeten bewijzen, is het volgende: Als $LK$ en $JK$ inderdaad cycloïden zijn, is het stuk $LQ$ langs de bovenste cycloïde opgeteld bij $QS$ ook precies gelijk is aan $4$? Dan is er dus inderdaad sprake van verkorting van de slinger zodat deze een cycloïde baan beschrijft.
Het bewijs
De bovenste cycloïde wordt gegeven door de draaiing tegen het plafond op hoogte $y=4$ van het bovenste ‘wiel’. Als de bovenste spaak gedraaid is over een hoek $\alpha$, is het middelpunt verplaatst van $M_1$ naar $M_2$. En er geldt $M_1 M_2 = \text{boog }TQ$. De onderste cycloïde wordt gegeven door de draaiing tegen de lijn op hoogte $y=2$ van het onderste wiel. Als de onderste spaak gedraaid is over een hoek $\alpha$, is het middelpunt verplaatst van $N_1$ naar $N_2$. En er geldt \(N_1 N_2 = \text{boog }VS\).
De figuur bevat twee congruente gelijkbenige driehoeken met basishoeken $\alpha/2$ en opstaande zijden $1$ (namelijk $\Delta Q M_2 R$ en $\Delta S N_2 R$). De lijn $RQ$ maakt met de verticaal een hoek $\alpha/2$. We weten (uit figuur 3 in deel II) dat de lijn $QR$ de raaklijn is in $Q$ aan de bovenste cycloïde. We bekijken nu de lijn $VS$.
Opgave 1
Toon in de tekening aan dat geldt: $\angle VSR = 90^o$.
Het lijkt erop dat de lijn $VS$ de cycloïde raakt in $S$. Dat is van belang om verder te komen maar dat moet nog wel aangetoond worden. We kijken daarvoor naar figuur 4.
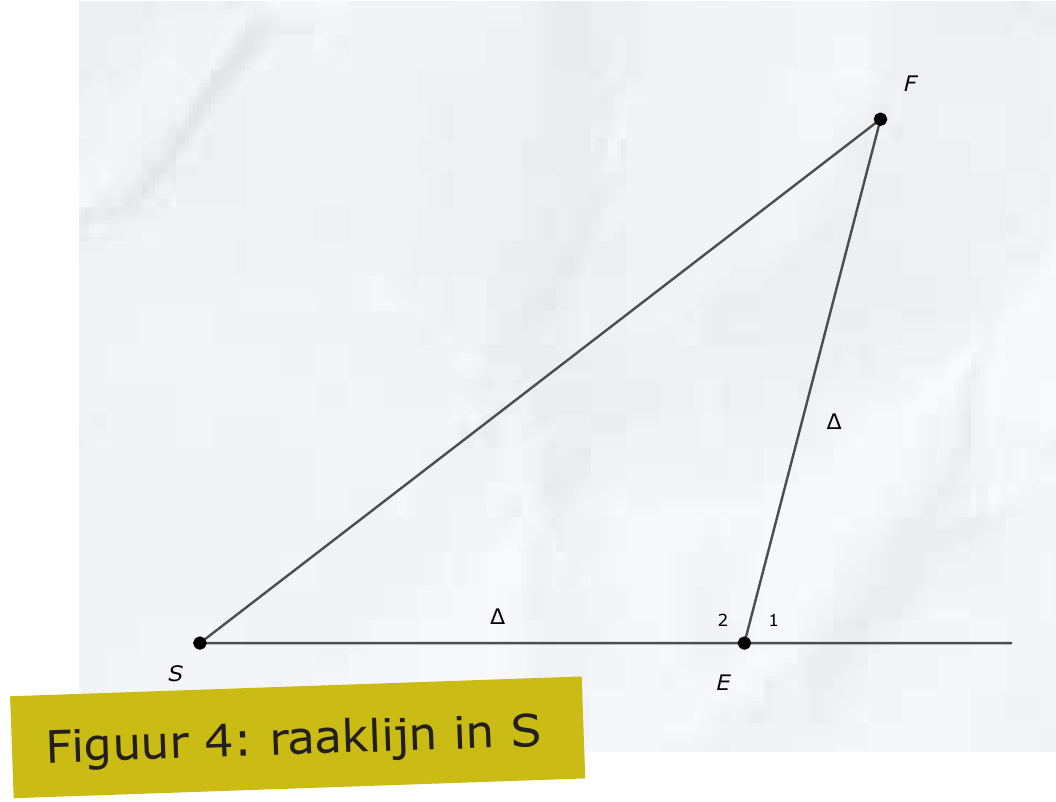
Het punt $S$ is hetzelfde punt als $S$ in figuur 3. Om de richting van de raaklijn aan de cycloïde in $S$ te vinden, draaien we het onderste ‘wiel’ over een heel klein hoekje. De horizontale verschuiving van het ‘wiel’ verplaatst $S$ naar $E$ over een klein stukje $\Delta$. De draaibeweging geeft ook een verschuiving $\Delta$ van $E$ naar $F$. Die staan kop-staart in de tekening, zodat de vectorsom $SF$ is. De richting van het minuscule stukje $SF$ is dan de richting van de raaklijn aan de cycloïde. Merk op dat de kleine verplaatsing $EF$ evenwijdig is aan de raaklijn in $S$ aan het ‘wiel’.
Opdracht 2
Toon in de tekeningen aan dat $EF$ een hoek $\alpha$ maakt met de horizontaal.
Opdracht 3
Toon aan dat lijn $VS$ de cycloïde raakt.
Conclusie
De belangrijke conclusie nu is: de raaklijn $QS$ in punt $Q$ aan de bovenste cycloïde staat loodrecht op de raaklijn in $S$ aan de onderste cycloïde. Als we nu van de raaklijn $QS$ alleen punt $S$ een microscopisch klein stukje verschuiven langs de onderste cycloïde naar $S’$, dan blijft de lengte van $QS$ gelijk omdat de hoek $90^o$ is. Het raakpunt $Q$ komt dan iets lager te liggen in $Q’$ op de bovenste cycloïde. Dan geldt: $QS=QQ’+Q’S’$. De lengte $Q’S’$ is dus iets korter geworden, maar datzelfde stukje ligt nu langs de bovenste cycloïde. Opnieuw geldt nu dat de $Q’S’$ loodrecht staat op de onderste cycloïde. Zo kunnen we natuurlijk stukje voor stukje de slinger iets korter maken, waarbij de rest van de slinger langs de bovenste cycloïde is gevleid. En omdat we zijn begonnen met een lengte $4$, blijft deze lengte steeds $4$.
We kunnen de redenering omdraaien. Neem een slinger van vaste lengte ($4$ in ons geval) met een massa $m$ aan het eind en laat de onderste cycloïde in gedachten weg. Dan zal bij een groter wordende uitwijking het wangetje (de bovenste cycloïde) het slingerdeel los van de cycloïde verkorten en de massa $m$ in $S$ zal dan precies de onderste cycloïde volgen en dus een isochrone slingerbeweging gaan uitvoeren, waarbij de maximale uitwijking er dus niet toe doet. Precies zoals Huygens het wilde.
Literatuur: Henk Broer, Hemelverschijnselen nabij de Horizon, Epsilon Uitgaven, nr. 77 (2013).
Bekijk oplossing