Opgave 1

$AB = BP = CP = DP = 1$ en $AC = BD = \sqrt{2}$. Dus $\angle APC$ en $\angle BPD$ zijn rechte hoeken met behulp van de omgekeerde stelling van Pythagoras. Dan moet gelden hoek $\alpha \le 45^{\rm o}$.

Opgave 2

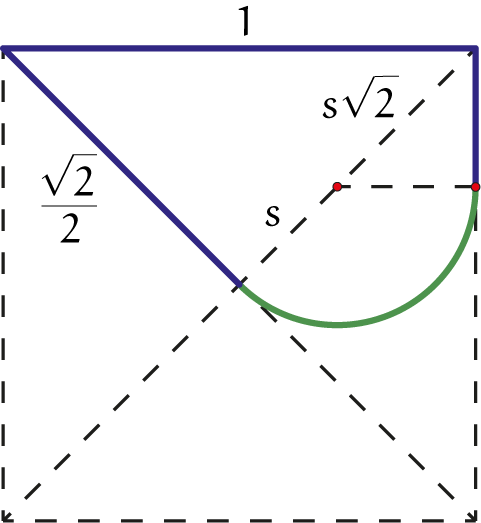
(zie de figuur): $s\sqrt{2} + s = \frac{\sqrt{2}}{2}$ en dus $s = 1-\frac{\sqrt{2}}{2}$.

Opgave 3

$AP=BP=CP=DP=EP=FP=\sqrt2$.

Opgave 4

Voor het geval $n=6$ krijgen we, op vergelijkbare wijze als in het geval $n=4$ de vergelijking $\frac{2s}{\sqrt{3}}+s=1$ en dus $s=2\sqrt{3}-3$.

Opgave 5

Laat $\beta = \left(90-\frac{180}{n}\right)^{\rm o}$. Dit is de waarde van de basishoeken in de $n$ gelijkbenige driehoeken. Dan zijn $AP=BP=CP=DP=\cdots=\frac{\sqrt{2}}{2\cos(\beta)}$.

Opgave 6

$$s=\frac{1}{2\cos(\beta)\left(1+\frac{1}{\sin(\beta)}\right)}$$