
Is het een cadeautje?
[oOO]
Wanneer je iets leuks koopt in de winkel word je vaak gevraagd of het een cadeautje is. Een cadeau moet namelijk een mooie verpakking krijgen, maar ik vind dat de mooiste verpakking er één is die je zelf maakt.
Ik heb twee kleinkinderen en ik wil hun allebei een cadeau geven. Ik heb nog geen idee wat het cadeau zou kunnen zijn, maar ik heb wel een idee over hoe de verpakking eruit moet zien.
Ik heb de verpakking wiskundig bedacht. De foto’s in figuur 1 laten een voorbeeld zien.
 |
 |
Figuur 1 |
|
Het is een huisje met vierkanten als muren en een dak van gelijkzijdige driehoeken. De vloer van het huisje is te zien in de tweede foto en wordt gevormd door vier stukken die over elkaar heen worden gevouwen. Het voorbeeld is uit één stuk papier gemaakt. In figuur 2 is een tekening van het patroon. De kleine driehoeken tussen de gelijkzijdige driehoeken worden naar binnen gevouwen terwijl alle punten $P$ bij elkaar komen om de top te vormen. De onderbroken lijnen laten zien hoe een cirkel wordt getekend die door het middelpunt van het vierkant gaat, één van de zijden raakt en zijn middelpunt heeft op een diagonaal. Op de gele vlakken komt lijm. Ik heb de doos dichtgemaakt met een veter aan de bovenkant.
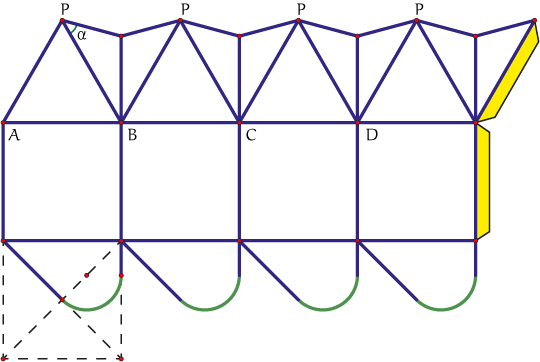
Figuur 2
Een paar berekeningen zijn nodig om deze constructie te maken:
Opgave 1Hoe groot zijn de hoeken $APC$ en $BPD$ in de gevouwen piramide en dus hoe klein moet hoek $\alpha$ zijn om genoeg ruimte te krijgen in de ingevouwen piramide? Opgave 2Als we ervan uit gaan dat de zijden van het vierkant lengte $1$ hebben, wat is dan de straal van de cirkelboog op de onderkant? |
 |
 |
Figuur 3 |
|
In het geval van een huisje met $6$ muren (figuur 3) leveren gelijkzijdige driehoeken geen puntig dak op. De driehoeken moeten hoger reiken en gelijkbenig worden. Nu is de zeshoekige dakrand $ABCDEF$. Ga er weer vanuit dat alle zijden van deze bovenrand lengte $1$ hebben.
Opgave 3Hoe lang moeten dan de lengtes $AP = BP = CP = DP = EP = FP$ zijn zodat de hoeken $APD$, $BPE$ en $CPF$ hetzelfde zijn als de hoeken $APC$ en $BPD$ in het eerste voorbeeld? Dan weten wij weer hoe klein hoek $\alpha$ moet zijn. Opgave 4Als we ervan uit gaan dat de zijden van de zeshoek lengte $1$ hebben, wat is dan nu de straal van de cirkelboog op de onderkant? |
Voor de liefhebbers blijft de algemene vraag hoe het zit bij een huisje met $n$ vierkante muren met zijden van lengte $1$.
Opgave 5Wat is dan de formule voor de lengte van de opstaande ribben van het dak als we dezelfde waarde voor hoek $\alpha$ willen gebruiken? Opgave 6Wat is dan de formule voor de straal van de cirkelboog op de onderkant? |
