Opgave 1

Het aantal factoren van $72 = (1 + $ de macht van $2)(1 + $ de macht van $3) = 4\times 3 = 12$.

Opgave 2

Een kwadraat heeft een oneven aantal factoren (zijn wortel vormt een paar met zichzelf) en dus moeten alle machten van zijn priemfactoren even zijn.

Opgave 3

$18x^2+75x+50=(3x+10)(6x+5)$

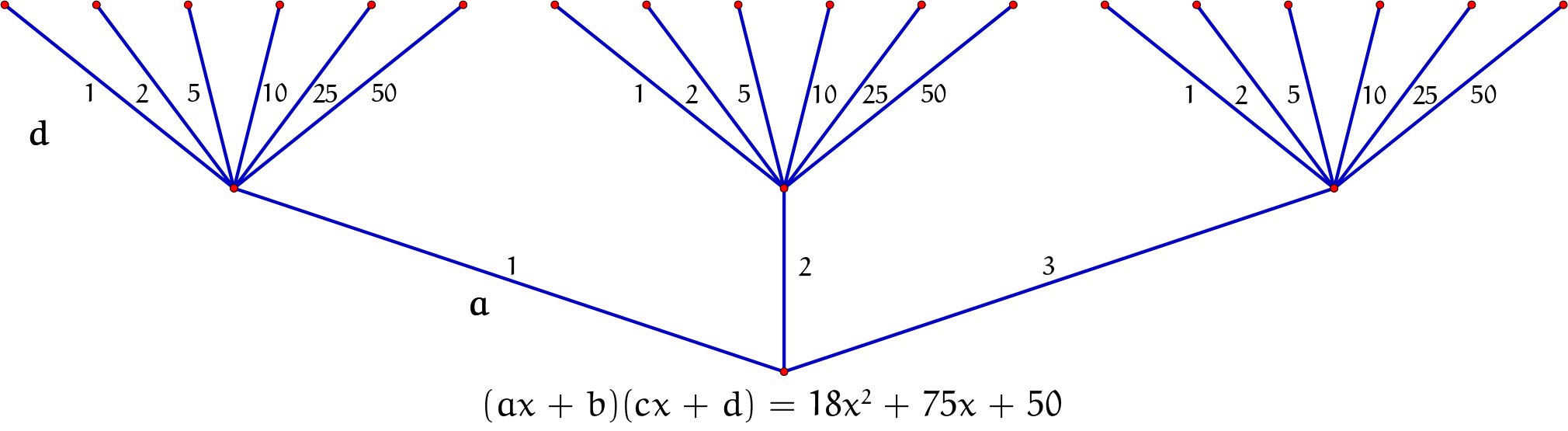
Opgave 4

$48=2^4\times3^1$ en heeft dus $10$ factoren. $300=2^2\times 3^1\times 5^2$ en heeft dus $18$ factoren. Er zijn $90$ combinaties van $a$ en $d$ en om te bepalen dat één van de uitdrukkingen niet ontbonden kan worden moet je alle $90$ bekijken. Dit is te veel gevraagd.

Opgave 5

Kijk eerst naar de ontbindingen in priemfactoren van $365$ en $385$ en het is makkelijk te zien dat de coëfficiënten van beide uitdrukkingen relatief priem zijn.

$48x^2+365x+300=(ax+b)(cx+d)=\left(ax+\frac{300}{d}\right)\left(\frac{48}{a}x+d\right)$ $\to ad+\frac{300\cdot 48}{ad}=365$ $\to (ad)^2-365\cdot(ad)+300\cdot 48=0$ en met je rekenmachientje kan je deze kwadratische vergelijking oplossen met $ad=45$ of $ad=320$. Elke gemeenschappelijke factor van $ad$ en $ac$ moet een factor van $a$ zijn want anders waren de coëfficiënten niet relatief priem, en elke factor van $a$ moet een gemeenschappelijke factor van $ad$ en $ac$ zijn.

Als $ad=45=3^2\times5$ en $ac=48=2^4\times 3$ dan moet $a=3$ en

Als $ad=320=2^5\times 2$ en $ac=48=2^4\times 3$ dan moet $a=2^4=16$.

Beide antwoorden leiden tot de ontbinding $48x^2+365x+300=(3x+20)(16x+15)$.

Als je dezelfde procedure uitvoert met $48x^2+385x+300$ dan is $ad$ geen geheel getal en is de ontbinding net mogelijk.

Opgave 6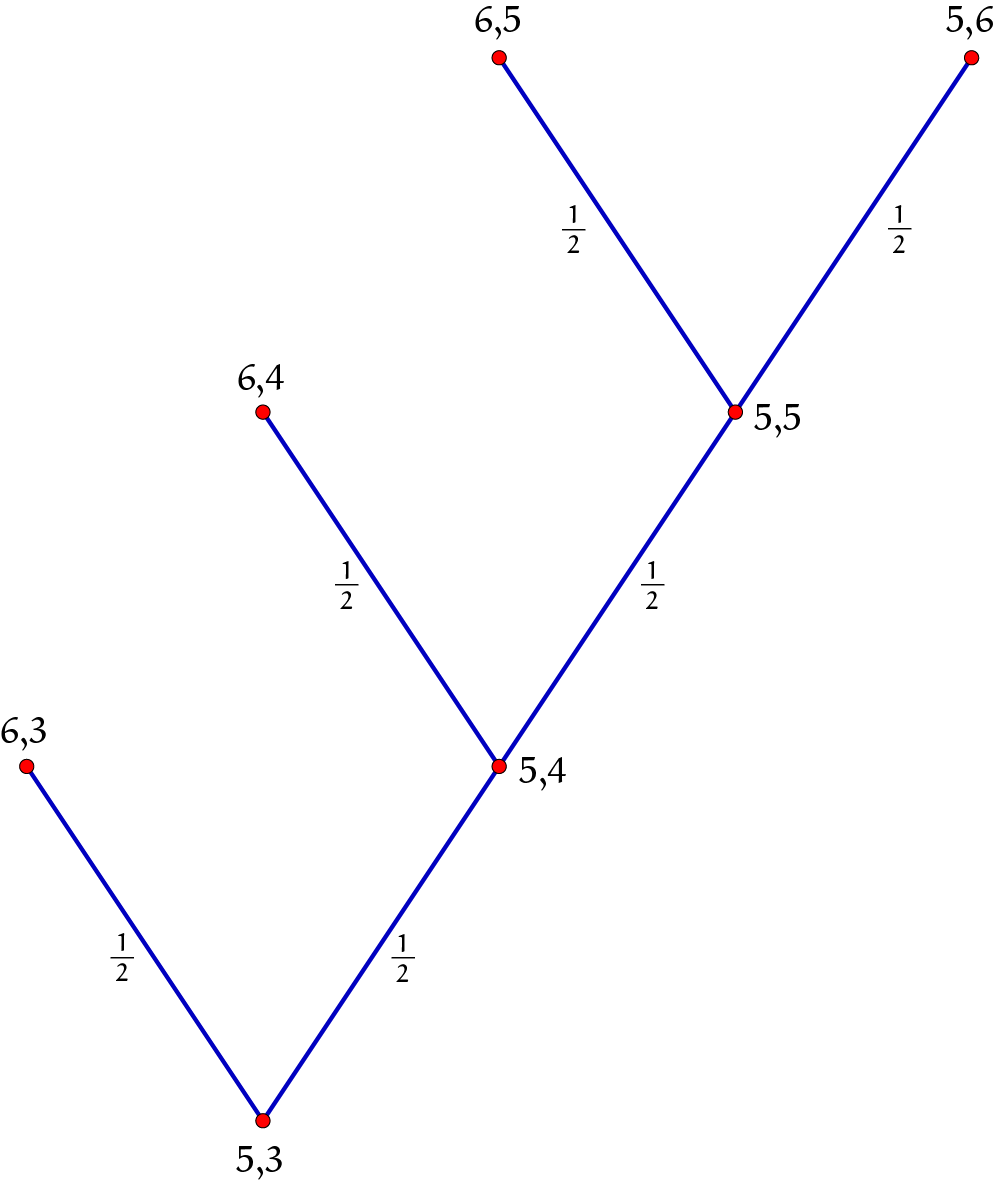

Stel dat het spel vele keren uitgespeeld had kunnen worden. Omdat het een kansspel was zouden we verwachten dat de speler met $5$ punten in de helft van de keren zou winnen in de volgende beurt, in een kwart van de keren zouden winnen na twee beurten en in een achtste van de keren zouden winnen na 3 beurten. Hij zou dus in zeven van de acht keren de pot winnen. Hier gaat de boom drie niveaus omhoog en op elke niveau is er een twee-vertakking (zie rechts)

Opgave 7

De eerlijke verdeling van de pot zou zijn in de verhouding $19:6:2$. Hier zijn er drie mogelijke voortzettingen die tot een verlenging kunnen leiden dus moet de boom vier lagen hoog gaan met drie-vertakkingen op elke niveau.

Opgave 8

Het is handig om eerst een tabel te maken met alle gegevens die je direct uit de lijst met feiten kan halen. Dan kan je de boom in gaan met het invullen van een aanname samen met al zijn consequenties. Nu zijn er drie mogelijkheden:

1. Je kan de puzzel afmaken
2. Je bereikt een tegenspraak en je aanname moet terugroepen worden, of
3. Je bent er nog niet uit en hebt geen tegenspraak bereikt en dus moet je een volgende aanname maken.

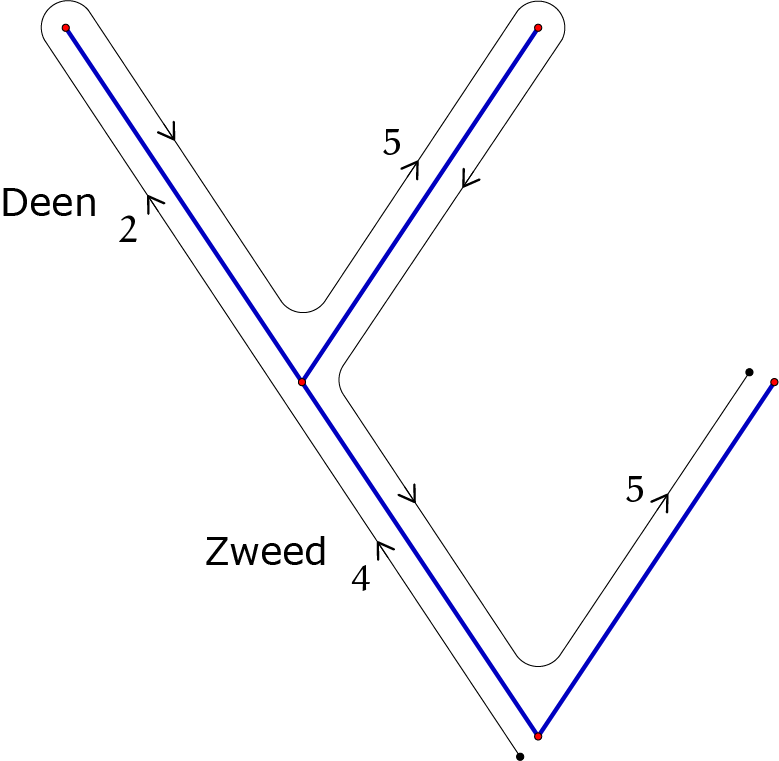Zo ga je verder totdat je de oplossing vindt. Je kan geluk hebben met een juiste aanname maar vroeg of laat komt het antwoord eruit. Hier is een poging te zien waar ik de boom in en uit moest gaan om het antwoord te vinden (deze methode is ook handig bij het oplossen van b.v. moeilijke killer sudoku’s).

$1$	$2$	$3$	$4$	$5$
$Noor$		$Brit$
		$Melk$	$Koffie$
$Dunhill$
	$Paarden$

 

Conclusie: De Duitser heeft een vis