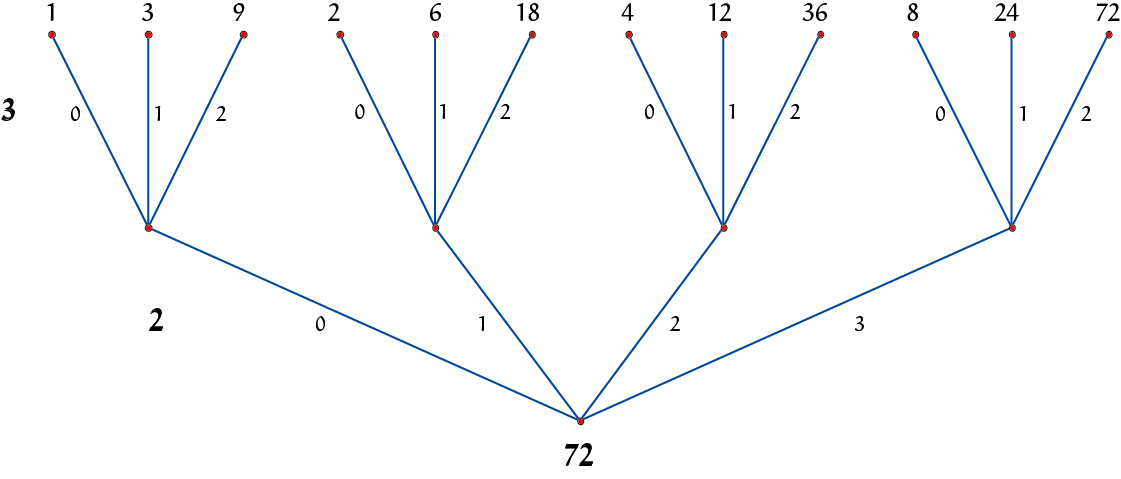
Hier is een simpel voorbeeld: een factorboom. Schrijf eerst het getal $72$ als product van zijn priemfactoren: $72 = 2^3 \times 3^2$. Alle factoren van $72$ hebben $0, 1, 2$, of $3$ factoren $2$ en $0, 1$, of $2$ factoren $3$, zoals te zien in bovenstaande figuur.

Opgave 1 Wat is het verband tussen de machten van $2$ en $3$ en het aantal factoren van $72$? Opgave 2 De factoren van $72$ komen in paren: $1 \times 72$, $2 \times 36$, etc. Wat is er speciaal aan het aantal factoren van een kwadraat en wat zegt dat over de machten van zijn priemfactoren?

Soms is het mogelijk om een uitdrukking zoals $18x^2 + 75x + 50$ op te splitsen in de vorm $(ax + b)(cx + d)$, met $a$, $b$, $c$ en $d$ gehele getallen. Dit noemen we ontbinden in factoren. Hier moet je eerst weten hoeveel factoren $18$ en $50$ hebben.

Ze hebben allebei $6$ factoren en door verdubbeling te vermijden zijn er $18$ verschillende combinaties voor $a$ en $d$, want $18$ heeft $3$ factorparen en $50$ heeft $6$ factoren. En als geen combinatie werkt weet je dat de uitdrukking niet valt op te splitsen. Een goede eerste stap is de relatief-priem-test: controleren of $18$, $75$ en $50$ relatief priem zijn. (Ze zijn relatief priem als $1$ het enige getal is dat deler is van alle drie.) Als de drie coëfficiënten niet relatief priem zijn kun je die gemeenschappelijke factor naar voren halen en alle getallen worden kleiner en het probleem dus makkelijker.

Opgave 3 Maak de boom van combinaties voor $a$ en $d$ en bepaal of $18x^2 + 75x + 50$ op te splitsen is.

Boomdiagrammen zijn handig maar soms zijn er zoveel mogelijkheden dat je gaat zoeken naar een snellere oplossing. Kijk bijvoorbeeld naar $48x^2 + 385x + 300$ en $48x^2 + 365x + 300$. Eén van deze uitdrukkingen kan opgesplitst worden en de andere niet.

Opgave 4 Hoeveel mogelijke combinaties voor $a$ en $d$ zouden er nu zijn?

Hier is een snellere manier om het antwoord te krijgen. Doe eerst de relatief-priem-test. Vervang dan $b$ en $c$ in $(ax + b)(cx + d)$ door uitdrukkingen in $a$ en $d$. 

Maak nu een kwadratische vergelijking voor ad en vind de mogelijke oplossingen. Hier is een rekenmachientje handig. Vergelijk $ad$ met $ac$ om de waarde van $a$ te bepalen waarna de rest volgt.

Opgave 5 Wat zijn nu de uitkomsten voor $48x^2 + 385x + 300$ en $48x^2 + 365x + 300$?

Wat is eerlijk?

Een andere situatie waarin een boomdiagram handig is geweest, was een belangrijk probleem in het begin van de geschiedenis van de kansrekening. Twee spelers zijn bezig met een kansspel en hebben afgesproken om de hele inzet toe te kennen aan diegene die het spel als eerste $6$ keer wint. Een speler heeft al $5$ keer gewonnen en de andere speler slechts $3$ keer. Het spel moest afgebroken worden. Laten we het spannender maken door te zeggen dat struikrovers in de buurt zijn en de twee spelers elkaar niet vertrouwen. Hoe moet de inzet op een eerlijke manier verdeeld worden? Beide spelers hadden uiteindelijk kunnen winnen maar één speler stond dik voor.

Opgave 6 Laat met een boomdiagram zien dat de verhouding $7 : 1$ een eerlijke verdeling zou zijn. Opgave 7 Wat zou de eerlijke verdeling zijn als drie spelers met een kansspel bezig zijn waar $6$ keer winnen beslissend is en het spel wordt gestopt met een tussenscore van $5 : 4 : 3$?

Hoor jij tot die 2%?

Einstein zou een keer beweerd hebben dat 98% van de mensheid het volgende probleem niet zou kunnen oplossen. Het probleem bestaat uit een lijst van beweringen over 5 mensen van 5 verschillende nationaliteiten.

Opgave 8 De vraag is: Wie heeft een vis als huisdier?  Hier zijn de aanwijzingen: De Brit woont in het rode huis De Zweed houdt honden als huisdier De Deen drinkt thee Het groene huis staat direct links van het witte huis De eigenaar van het groene huis drinkt koffie De persoon die Pall Mall rookt, fokt vogels De eigenaar van het gele huis rookt Dunhill De man die in het middelste huis woont, drinkt melk De Noor woont in het eerste huis De man die Blends rookt, woont naast de man die katten houdt De man die paarden houdt, woont naast de man die Dunhill rookt De eigenaar die Bleu Masters rookt, drinkt bier De Duitser rookt Prince De Noor woont naast het blauwe huis De man die Blends rookt heeft een buurman die water drinkt

Ze wonen in huizen van verschillende kleuren, houden verschillende huisdieren en hebben verschillende drank- en rookgewoontes. (Er zijn een paar details die laten zien dat deze puzzel in het verre verleden werd bedacht. Waarom zijn alle eigenaars mannen en waarom roken ze allemaal als ketters?). Hier kan een tabel heel handig zijn en dan een boomdiagram om systematisch de mogelijkheden te onderzoeken. Hoewel we allemaal onszelf al hadden ingedeeld in de top 2% zou het oplossen van dit probleem een mooie bevestiging kunnen zijn. 

Bekijk oplossing