Opgave 1

Hoe je het ook doet, je zou $x = 3$ en $x = -13$ moeten krijgen als oplossingen.

Opgave 3

Oplossing: Wij zoeken de $x,$ Al-Khwarizmi vraagt naar de $x^2.$ Hij vindt wel dezelfde positieve oplossing, $3.$ Hij vindt de negatieve oplossing niet, wat logisch is, aangezien je die niet als een lengte van een lijnstuk kunt zien. (Al-Khwarizmi kende overigens nog geen negatieve getallen.)

Opgave 5

1. Nog steeds $39.$
2. Die hoek is een vierkant van $5$ bij $5$ en heeft dus oppervlakte $25.$ Het grote vierkant heeft dus oppervlakte $39 + 25 = 64.$
3. De zijde van het grote vierkant is dus $8$ en je ziet dat $x = 3.$

Opgave 6

De hoekjes zijn nu alle vier $(2{,}5)^2 = 6{,}25,$ dus in totaal komt er $4 \cdot 6{,}25 = 25$ bij. Het grote vierkant heeft dus oppervlakte $39 + 25 = 64,$ de zijden zijn ook nu $x + 5,$ dus we vinden weer dat $x + 5 = 8$ dus $x = 3.$

Opgave 7

$x^2 + 10x = 39$

$(x + 5)^2 = 39 + 5^2$

$(x + 5)^2 = 64$

$x + 5 = 8$ of $x + 5 = -8$

$x = 3$ of $x = -13$

Je ziet dat de stappen bij de positieve oplossing precies hetzelfde zijn als die van Al-Khwarizmi: het halveren van de $10,$ je krijgt het kwadraat van $x+5$ dat gelijk is aan $64,$ enzovoorts.

Opgave 8

Eerste vergelijking: $x + 2 = 5$ of $x + 2 = -5,$ dus $x = 3$ of $x = -7.$

Tweede vergelijking: $x - 4 = 10$ of $x - 4 = -10,$ dus $x = 14$ of $x = -6.$

Opgave 9

1. Als je $(x + \dots)^2$ uitwerkt, krijg je altijd ook nog een getal als term, namelijk het kwadraat van het getal op de puntjes.
2. Daar moet een $5$ staan, want als je dan de haakjes uitwerkt krijg je $x^2 + 10x + 25.$

Opgave 10

1. Op de puntjes moet steeds de helft van de coëfficiënt van de $x,$ want dan krijg je weer het dubbele daarvan voor de $x$  als je de haakjes uitwerkt.
2. $(x + 2)^2 = 81,$ dus $x + 2 = \pm 9,$ dus $x = 7$ of $x = -11.$
   $(x - 6)^2 = 81,$ dus $x - 6 = \pm 9,$ dus $x = 15$ of $x = -3.$

Opgave 12

We krijgen een rechthoek van $x$ bij $x + 7$ die als oppervlakte $60$ heeft. Die rechthoek kunnen we opdelen in een vierkant van $x$ bij $x$ en een rechthoek van $x$ bij $7,$ net zoals in Al-Khwarizmi's voorbeeld. Als we het recept van Al-Khwarizmi volgen, moeten we de $7$ in tweeën delen, dat wordt $3{,}5.$ Een rechthoek van $3{,}5$ bij $x$ halen we weg en die plakken we onder het vierkant van $x$ bij $x,$ de missende hoek rechtsonder kunnen we opvullen met een vierkantje van $3{,}5$ bij $3{,}5,$ dus oppervlakte $(3{,}5)^2 = 12{,}25.$ Dan hebben we een groot vierkant met een oppervlakte van $60 + 12{,}25 = 72{,}25$ en een zijde van $x + 3{,}5.$ Omdat $\sqrt{72{,}25} = 8{,}5$ geldt dus $x + 3{,}5 = 8{,}5,$ dus $x = 5.$ De andere zijde van de rechthoek is dan dus $12.$ We zien deze stappen precies terug in het Babylonische recept.

Opgave 13

1. $x^2 + x = 0{,}75$
2. Je kunt een rechthoek van oppervlakte $x$ maken door de ene zijde lengte $x$ te geven en de andere zijde lengte $1.$

Opgave 14

Dit is weer precies het probleem van Al-Khwarizmi, maar dan met een vierkant van $x$ bij $x$ en een rechthoek van $x$ bij $1.$ We krijgen dan een "groot" vierkant met zijde $x + 0{,}5$ en oppervlakte $0{,}75 + (0{,}5)^2 = 1,$ dus zijde $1,$ dus $x = 0{,}5.$

Opgave 15

1. $x^2 - x = 870$
2. Het gaat weer over een vierkant waarvan de zijde onbekend is. We moeten er nu echter de zijde van afhalen in plaats van erbij doen. We krijgen dus wel weer met een zelfde dimensieprobleem te maken, dat we weer kunnen oplossen door een rechthoek van $x$ bij $1$ te gebruiken.

Opgave 16

Hier hoort figuur 3a bij.

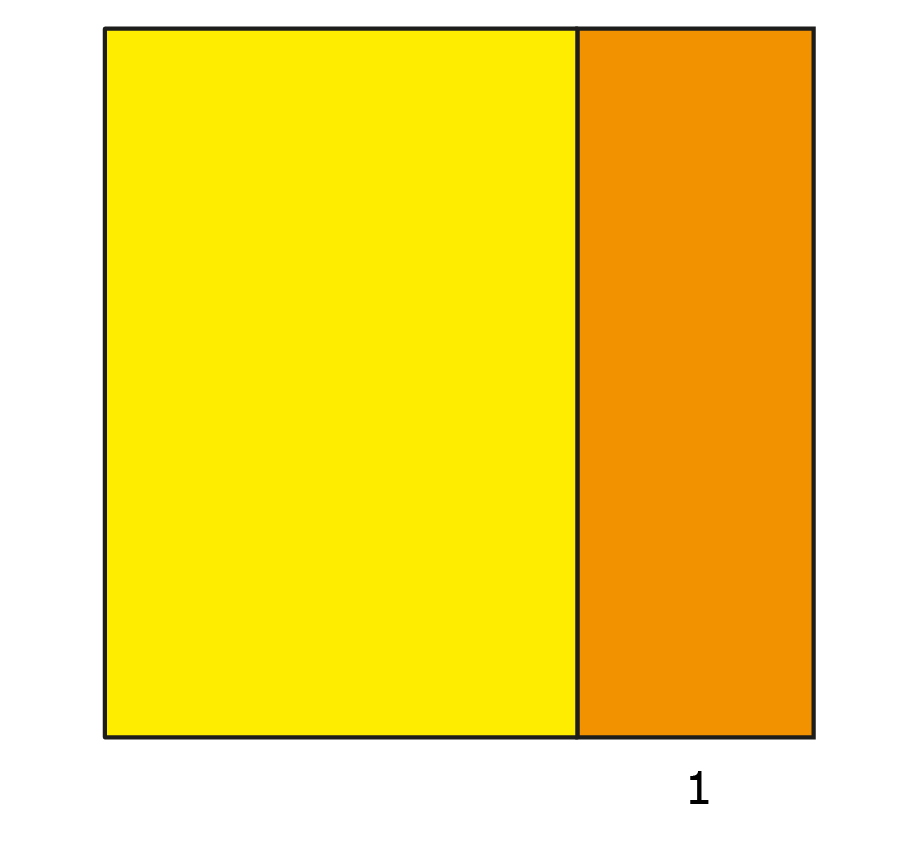
Dit is een vierkant van $x$ bij $x$ waar een rechthoek van $1$ bij $x$ is afgehaald. We weten dat de oppervlakte van het gele deel $870$ is. Het recept heeft het ook hier over het halveren van de $1,$ dus die rechthoek verdelen we in twee gelijke delen (zie figuur 3b).

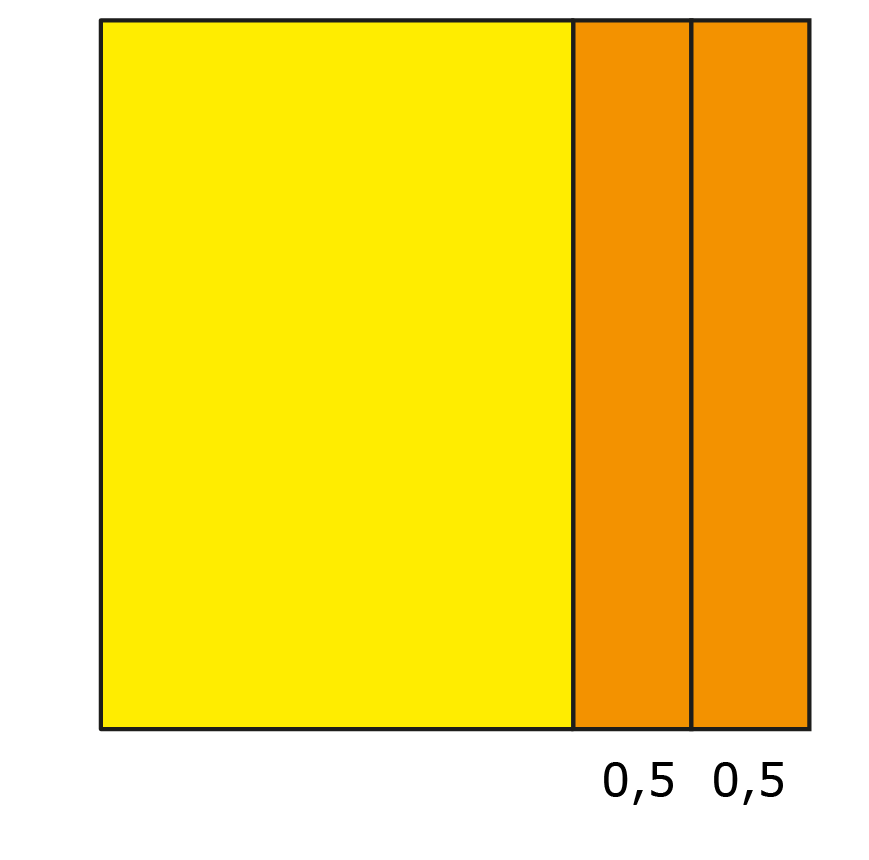
Nu is de vraag wat er met die delen gebeuren moet om er een nieuw (in dit geval: kleiner) vierkant te maken. We kunnen de linkerhelft van de oranje rechthoek horizontaal leggen, dan houden we linksonder in ieder geval een vierkant over (zie figuur 3c).

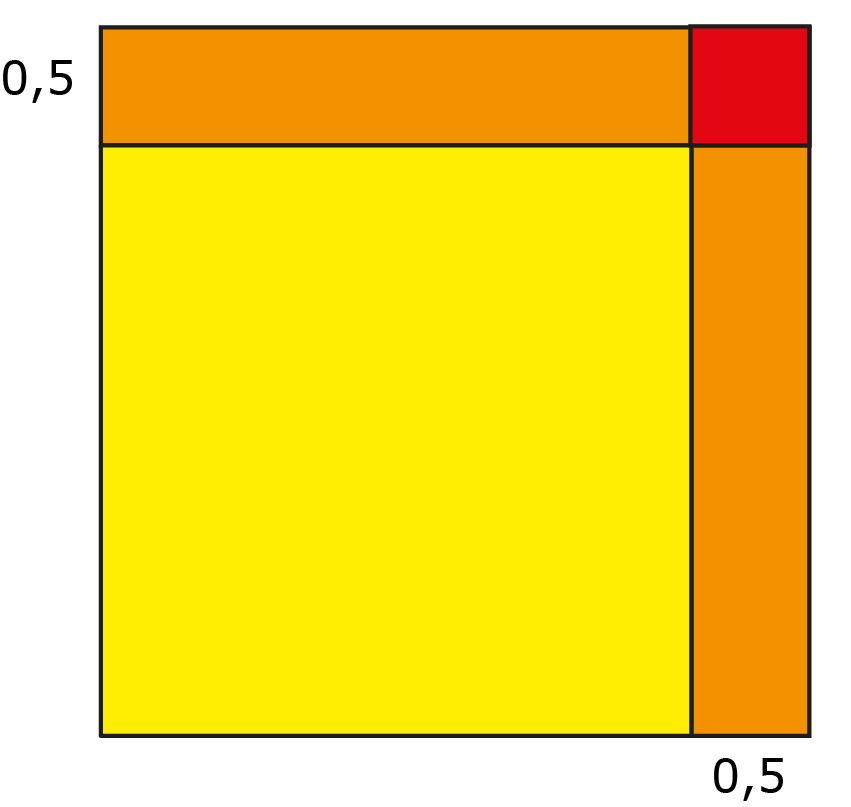
Alleen: je ziet dat de twee rechthoeken die verwijderd zijn elkaar overlappen in de hoek rechtsboven. De oppervlakte van het vierkant linksonder is nu dus $870 + (0{,}5)^2 = 870{,}25,$ we hebben dat vierkantje er tenslotte één keer minder afgetrokken dan in het originele probleem. De zijde van het vierkant is gelijk aan $x - 0{,}5.$ Dus ook nu vinden we dat $x-0,5 = \sqrt{870{,}25} = 29{,}5$, dus $x = 30.$

Opgave 17

$(x - 5)^2 = -21 + 25 = 4,$ dus $x - 5 = \pm 2,$ dus $x = 7$ of $x = 3.$

Opgave 18

$(x - 0{,}5)^2 = 870 + (0{,}5)^2 = 870{,}25,$ dus $x-0{,}5 = \pm \sqrt{870{,}25} = \pm 29{,}5$, dus $x = 30$ of $x = -29.$ De Babyloniërs zullen alleen de positieve oplossing vinden, en omdat de vraag over een vierkantszijde gaat is dat ook de enige kloppende hier.

De stappen zijn precies die van het meetkundige recept. Merk op dat het optellen van die $(0{,}5)^2$ hier vanzelf volgt uit de algebra: die komt nu voort uit het feit dat bij haakjes uitwerken aan de linkerkant een $(-0{,}5)^2 +(0{,}5)^2$ ontstaat. Bij de meetkundige oplossing kwam dat doordat we een vierkantje een keer te weinig hadden afgetrokken, zodat dat er weer bij moest.

Opgave 19

$$x^2 + \frac{b}{a}x=-\frac{c}{a}.$$

Kwadraat afsplitsen geeft nu (waarbij we weer de helft van de coëfficiënt van de lineaire term nemen):

$$\left(x+\frac{b}{2a}\right)^2 = -\frac{c}{a}+\left(\frac{b}{2a}\right)^2.$$

Voor het gemak werken we rechts de haakjes uit en maken we de breuken gelijknamig:

$$-\frac{c}{a}+\left(\frac{b}{2a}\right)^2 = -\frac{c}{a}+\frac{b^2}{4a^2} = \frac{-4ac}{4a^2}+\frac{b^2}{4a^2} = \frac{-4ac+b^2}{4a^2} .$$

In de teller herken je de discriminant al! Het is dus handig om de termen even om te wisselen en we concluderen:

$$\left(x+\frac{b}{2a}\right)^2 = \frac{b^2-4ac}{4a^2}.$$

Nu lossen we de vergelijking "gewoon" op door te worteltrekken:

$$x+\frac{b}{2a}=\pm\sqrt{\frac{b^2-4ac}{4a^2}}.$$

Nu trekken we aan beide kanten $\frac{b}{2a}$ af en dan vinden we de oplossing:

$$x=-\frac{b}{2a}\pm \sqrt{\frac{b^2-4ac}{4a^2}}.$$

Nu is een klein beetje herschrijven genoeg:

$$x=-\frac{b}{2a}\pm\frac{\sqrt{b^2-4ac}}{\sqrt{4a^2}}=\frac{-b}{2a}\pm\frac{\sqrt{b^2-4ac}}{2a}=\frac{-b\pm\sqrt{b^2-4ac}}{2a}.$$