Opgave 1

Het volume $V$ is een functie van $s$. $V(s)=\frac{\pi\cdot s^2\cdot\sqrt{r^2-s^2}}{3}$. Neem de afgeleide hiervan en stel hem gelijk aan $0$. Dan is $s=\frac{\sqrt{6}}{3}\cdot r$.

De oppervlakte = $\pi\cdot r^2\cdot\frac{2\cdot\pi\cdot s}{2\cdot\pi\cdot r}=\pi\cdot r\cdot s=\pi\cdot\frac{\sqrt{6}}{3}\cdot r^2$.

Opgave 2

De volume-functie is nu $V(s)=\frac{2\cdot s^2\cdot\sqrt{r^2-s^2}}{3}$. Neem weer de afgeleide en stel hem gelijk aan $0$. Wederom is $s=\frac{\sqrt{6}}{3}\cdot r$.

Opgave 3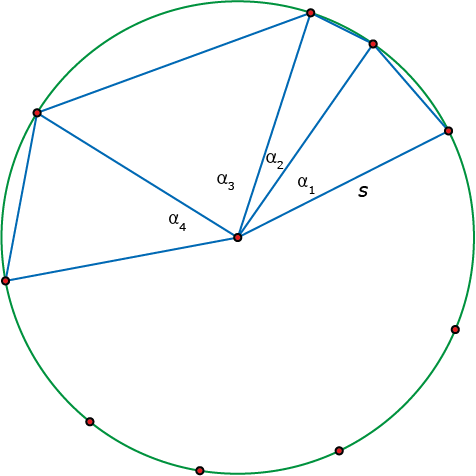

De oppervlakte van de vloer is $s^2\cdot\tfrac{1}{2}\cdot\left(\sin(\alpha_1)+\sin(\alpha_2)+\sin(\alpha_3)+\dots+\sin(\alpha_n)\right)$
waar $k=\tfrac{1}{2}\cdot\left(\sin(\alpha_1)+\sin(\alpha_2)+\sin(\alpha_3)+\dots+\sin(\alpha_n)\right)$.

Opgave 4

De waarde van $k$ doet er niet toe, als de afgeleide gelijk aan nul wordt gesteld rolt er weer uit $s=\frac{\sqrt{6}}{3}\cdot r$.

Opgave 5

Omdat de vloer meer en meer op een cirkel lijkt gaat de waarde van $k$ naar $\pi$. Ook kan je een gedachten experiment doen met veel palen allemaal op gelijke afstand. Dan met $n$ palen is $k=\frac{n\cdot\sin\left(\tfrac{2\pi}{n}\right)}{2}$ en $\displaystyle \lim_{n \to \infty}\frac{n\cdot\sin\left(\tfrac{2\pi}{n}\right)}{2}=\displaystyle \lim_{n \to \infty}\frac{2\pi}{n}\cdot\frac{n}{2}\cdot\frac{\sin\left(\tfrac{2\pi}{n}\right)}{\left(\tfrac{2\pi}{n}\right)}=\pi\cdot\displaystyle \lim_{n \to \infty}\frac{\sin\left(\tfrac{2\pi}{n}\right)}{\left(\tfrac{2\pi}{n}\right)}=\pi$.