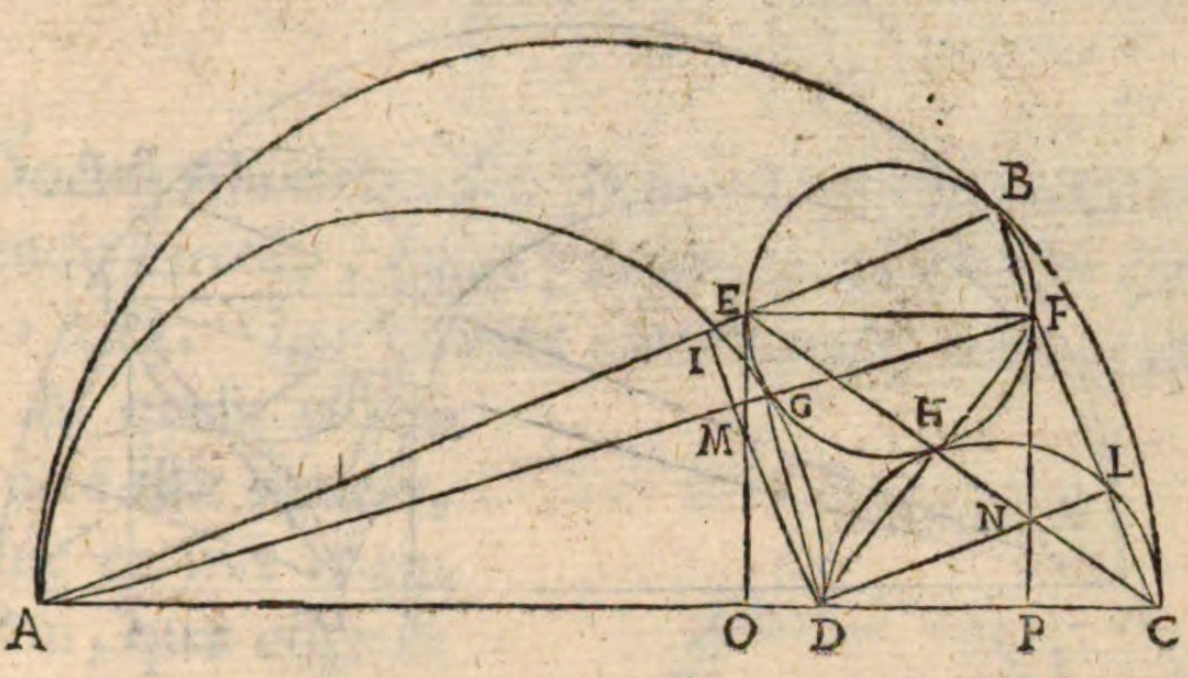
Archimedes van Syracuse, die leefde in de derde eeuw voor Christus, is de vermoedelijke auteur van een boek over eigenschappen van cirkels, het Boek van de hulpstellingen, of Liber assumptorum. We zijn niet helemaal zeker dat hij inderdaad de auteur is, want er is geen origineel exemplaar van het boek dat de tand des tijds heeft doorstaan. Er is wel een oude Arabische en een Latijnse vertaling, die laatste dateert van 1661. In dit artikel zijn enkele figuren opgenomen uit deze vertaling. Het boek bevat 15 lemma’s (of hulpstellingen) die verband houden met cirkels, en we willen het hier hebben over drie ervan, die een speciale meetkundige figuur bevatten die arbelos genoemd wordt. Arbelos is Grieks voor schoenmakersmes, en, zoals de naam doet vermoeden is dit een mes dat (toen en ook nu nog) wordt gebruikt door de schoenmaker. In figuur 2 zie je er een.

In essentie is een arbelos een gebied begrensd door drie halve cirkels, waarvan de middelpunten op dezelfde rechte liggen, en die elkaar onderling raken zoals in figuur 3. De arbelos is het gekleurde deel. Je herkent hierin de vorm van het kunstwerk in figuur 1.

Als de twee kleine cirkels even groot zijn, dan lijkt de figuur wel wat op de vorm van het schoenmakersmes.

Lemma 4

Het eerste lemma uit het boek waarin de arbelos voorkomt is lemma 4. De bijhorende figuur is figuur 4a.

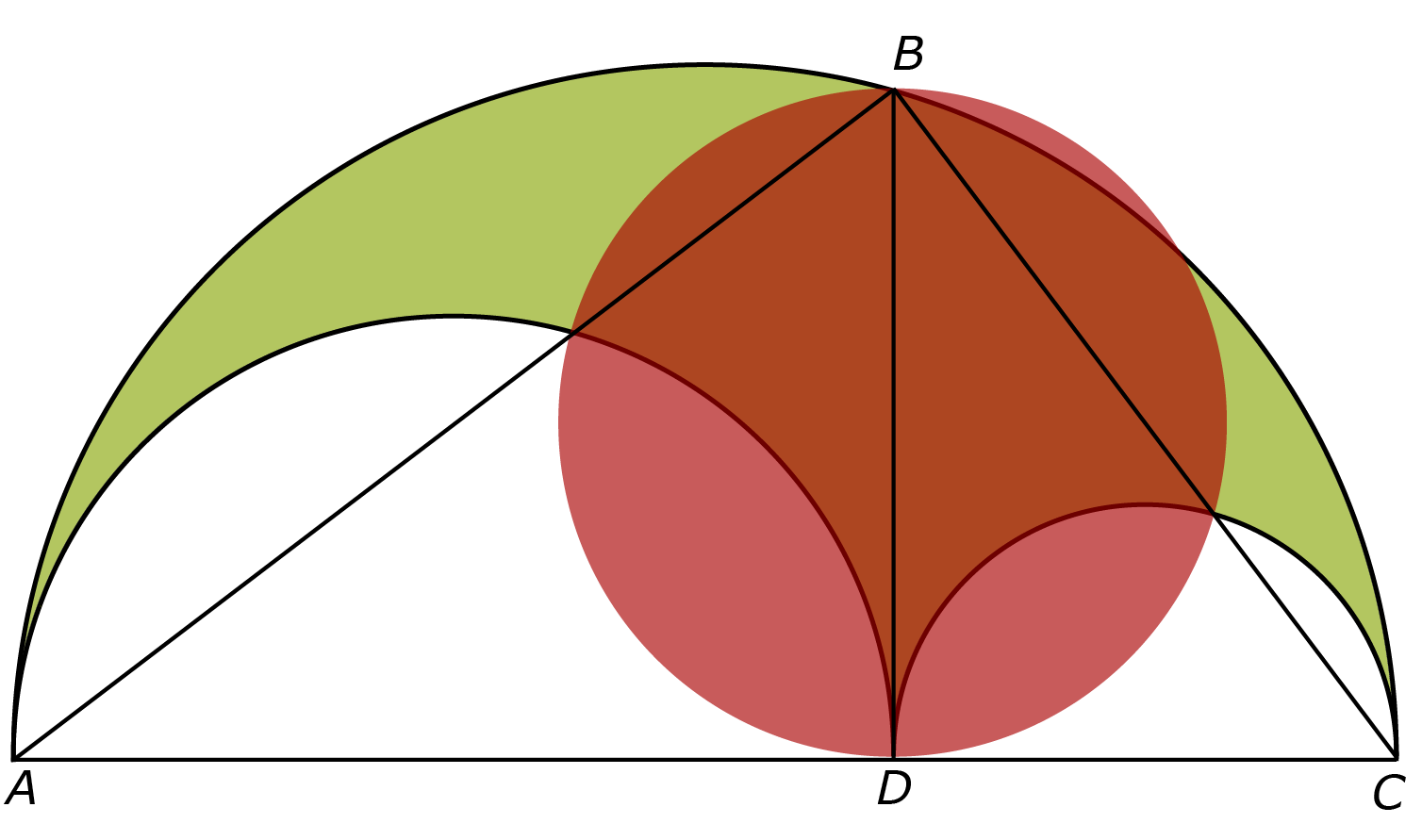
Lemma 4 zegt het volgende. We nemen het lijnstuk $BD$ dat raakt aan de twee kleine cirkels in hun raakpunt en loopt tot aan de grote cirkel. Als we een cirkel construeren met $BD$ als diameter (zie figuur 4a), dan is de oppervlakte van die cirkel (het gebied in het rood) gelijk aan de oppervlakte van de arbelos. Merk op dat $BD$ loodrecht staat op $AC$, door de vorm van de arbelos.

Opgave 1

Bewijs dit. (Zie ook Pythagorasolympiade, opgave 358, Pythagoras 56-6, juni 2017)

• Bereken eerst de oppervlakte van de arbelos. Veronderstel hierbij dat de straal van de kleine cirkel met diameter $DC$ gelijk is aan $r_1$, dat de straal van de cirkel met diameter $AD$ gelijk is aan $r_2$. De straal van de grote cirkel is dan gelijk aan $r_1 + r_2$.
• Bereken nu de lengte van het lijnstuk $BD$, en hiermee de oppervlakte van de rode cirkel.
  Tip: we weten dat de $\Delta ABC$ een rechte hoek heeft in $B$. Dit is een gevolg van de stelling van Thales: een omtrekshoek is de helft van de bijhorende middelpuntshoek.

Lemma 5

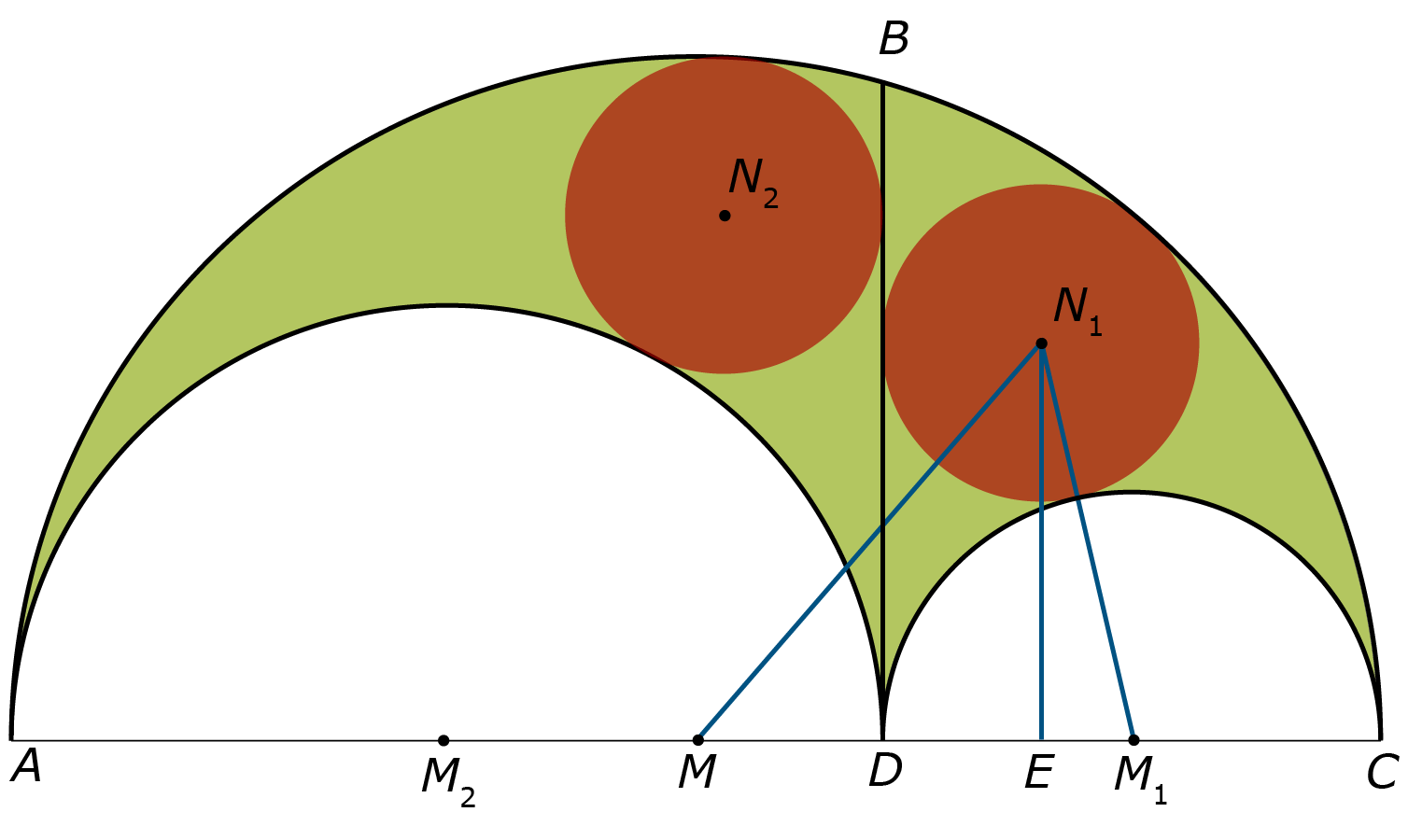
Het tweede lemma over de arbelos introduceert wat men noemt de cirkels van Archimedes. Zie figuur 5a, de ingeschreven cirkels van de twee helften van de arbelos die raken aan het lijnstuk $BD$.

We werken verder met het lijnstuk $BD$ uit het vorige lemma, en construeren links en rechts ervan 2 cirkels die zoals in de figuur raken aan dit lijnstuk en aan beide cirkels. Archimedes bewees dat deze nieuwe cirkels even groot zijn, en hij berekende ook de straal ervan. Deze cirkels worden dan ook soms de tweelingcirkels van Archimedes genoemd.

Veel meer dan de stelling van Pythagoras en enkele bekende eigenschappen van cirkels hebben we hiervoor niet nodig.

Opgave 2

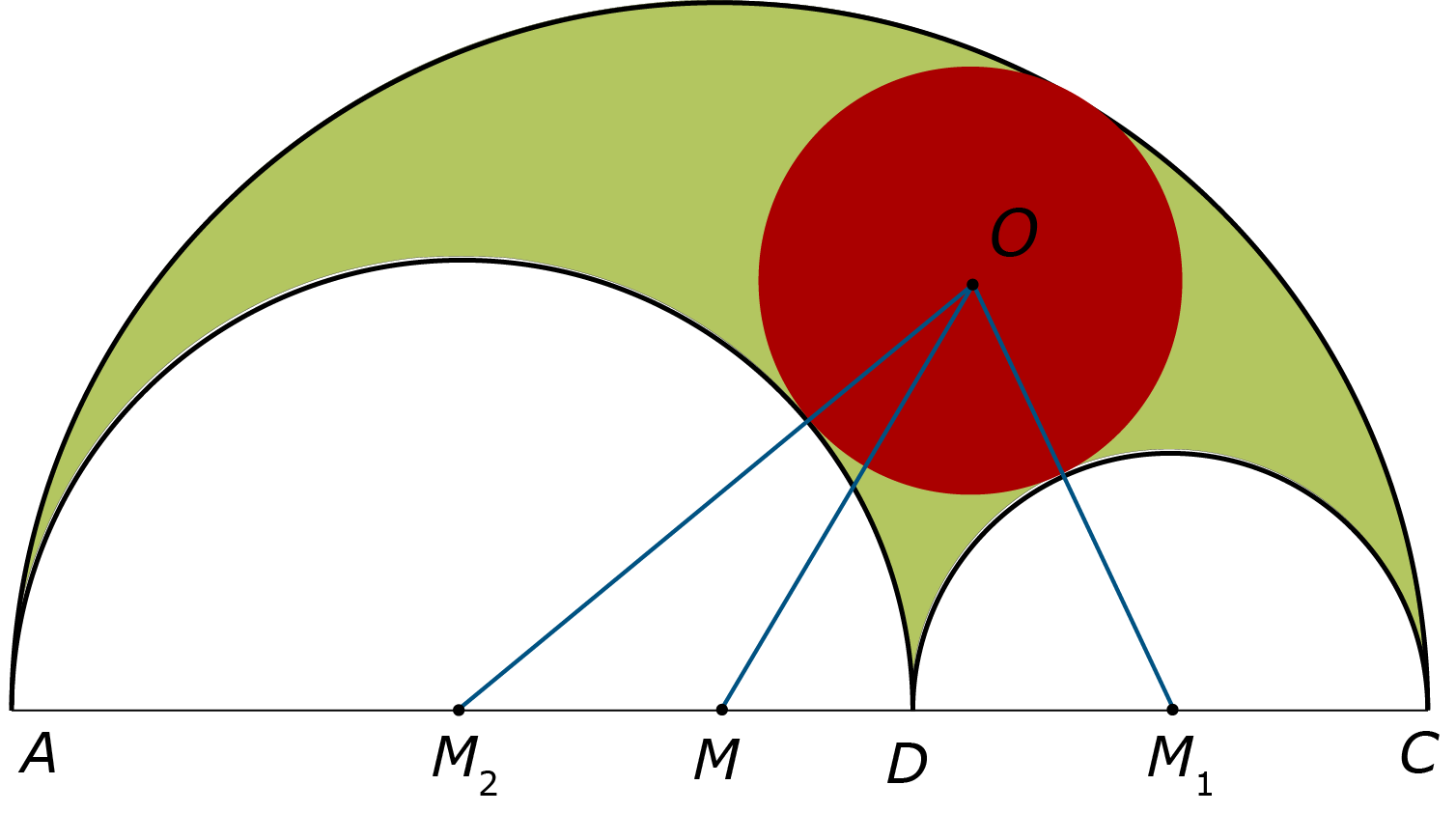
Bereken de straal r van de tweelingcirkel met middelpunt $N_1$ (zie figuur 5a). $M, M_1$ en $M_2$ zijn de middelpunten van de drie halve cirkels van de arbelos. We doen het in stappen:

• Bepaal de lengte van het lijnstuk $M_1N_1$ en van het lijnstuk $MN_1$.

• Het punt E is het voetpunt van de loodlijn door $N_1$ op het lijnstuk $AC$. Bepaal de lengte van het lijnstuk $EM_1$ en het lijnstuk $EM$.

• Bepaal uit het vorige op twee manieren de lengte van het lijnstuk $EN_1$ en leid hieruit de waarde van $r$ af.

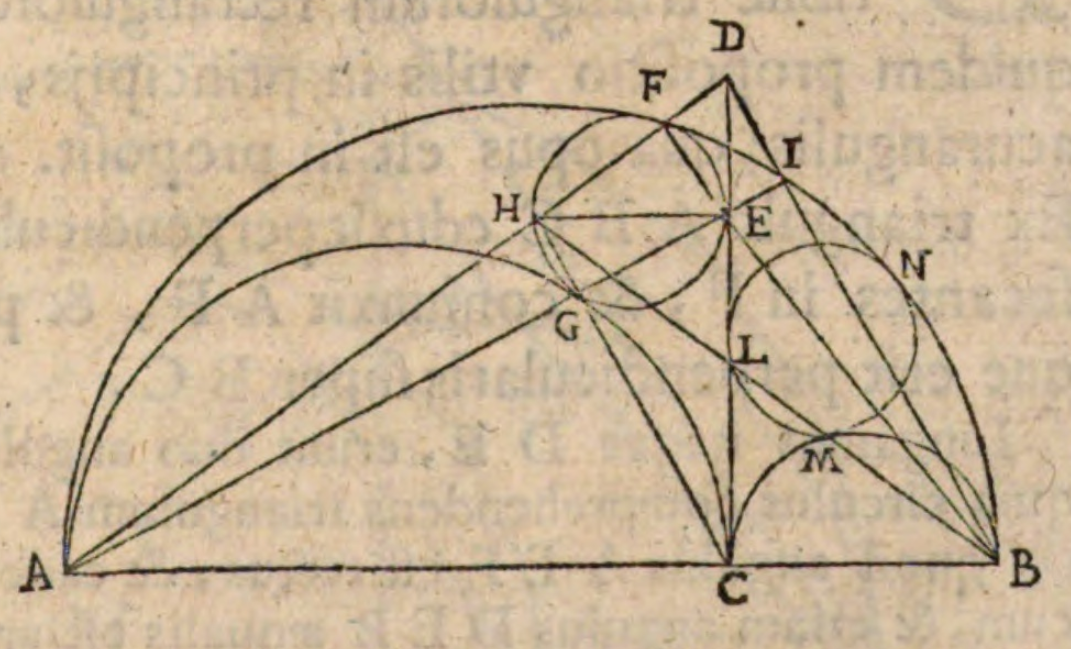
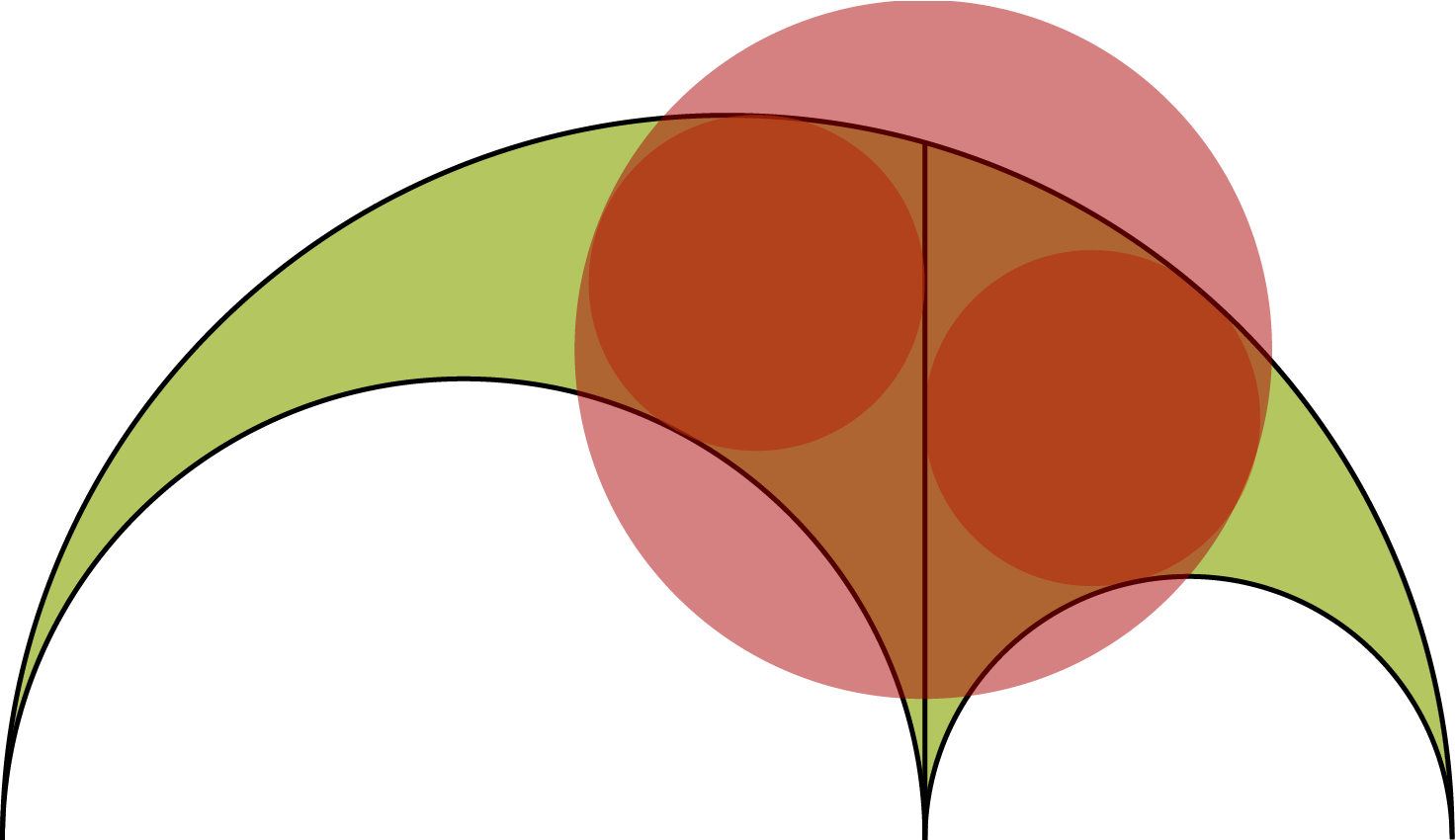
Als we nu hetzelfde doen voor de andere tweelingcirkel, dan vinden we hetzelfde resultaat. Het bewijs van Archimedes ging anders, zoals je kan zien aan de hulplijntjes in figuur 5b. We kunnen dit lemma gebruiken om het volgende te bewijzen (zie figuur 6): als we de cirkel construeren die de beide cirkels van Archimedes perfect omsluit, dan blijkt deze even groot te zijn als de cirkel uit lemma 4! Dit resultaat is recent, uit de tweede helft van de twintigste eeuw. De vinder was Leon Bankoff, een tandarts uit Los Angeles die in zijn vrije tijd gezorgd heeft voor een heropleving van de arbelos en zijn eigenschappen.

Lemma 6

Het derde lemma over de arbelos gaat over de cirkel die raakt aan de drie gegeven cirkels: zie figuur 7.

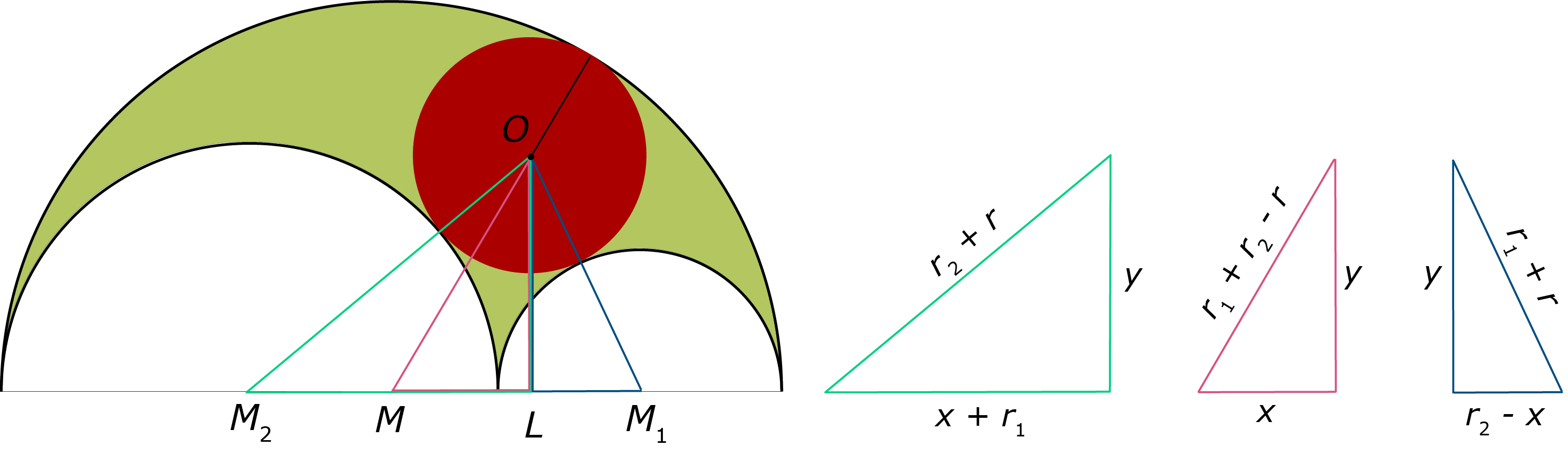
In lemma 6 stelt Archimedes de vraag: wat is de verhouding van de diameter van de nieuwe cirkel tot de diameter van de grootste cirkel? De afleiding die in het Boek van de hulpstellingen staat, is een stuk lastiger dan de andere. Maar je kan het ook met de stelling van Pythagoras en wat rekenwerk klaar krijgen. We veronderstellen dat de straal van de nieuwe (roodgekleurde) cirkel gelijk is aan $r$. In figuur 8 staat het lijnstuk $OL$ loodrecht op de basislijn. Als we de lengte van het lijnstuk $ML$ gelijk nemen aan $x$, en de lengte van $LO$ voorstellen door $y$, dan kunnen we in de figuur drie rechthoekige driehoeken zien waarvan we de drie zijden kennen (zie rechts in de figuur).

Opgave 3

Bereken de straal r van de rode cirkel in figuur 8 in functie van $r_1$ en $r_2$. Pas hiervoor in elk van de drie rechthoekige driehoeken de stelling van Pythagoras toe. Door $x$ en $y$ te elimineren tussen deze vergelijkingen, krijg je het gevraagde.

De verhouding waar lemma 6 het over heeft, is dus:

$$\frac{r}{r_1+r_2} = \frac{r_1r_2}{r^2_1+r_1r_2+r^2_2}.$$

De cirkelstelling van Descartes

In Pythagoras 51-5 (april 2012) hebben we verteld over een formule waaraan de stralen van vier cirkels die elkaar alle vier raken, moeten voldoen. Deze formule, die we danken aan René Descartes en de naam cirkelstelling van Descartes draagt, zegt het volgende: voor vier cirkels met stralen $r_1, r_2, r_3$ en $r_4$ die elkaar raken, geldt dat

$$\frac{1}{r^2_1} + \frac{1}{r^2_2} + \frac{1}{r^2_3} + \frac{1}{r^2_4} = \frac{1}{2}\left(\frac{1}{r_1} + \frac{1}{r_2} + \frac{1}{r_3} + \frac{1}{r_4} \right)^2$$

Lemma 6 van Archimedes is een voorloper van deze cirkelstelling. En we kunnen deze stelling gebruiken om lemma 6 te bewijzen. Een belangrijke opmerking hierbij: de drie kleinere cirkels raken de grootste cirkel inwendig: je moet dan in de formule de straal van de grootste cirkel met een minteken schrijven. Herinner je dat $r$ de straal van de rode cirkel is. Dan wordt de formule dus:

$$\frac{1}{r^2_1} + \frac{1}{r^2_2} + \frac{1}{(-(r_1+r_2))^2}+\frac{1}{r^2} = \frac{1}{2}\left(\frac{1}{r_1} + \frac{1}{r_2} - \frac{1}{r_1+r_2} + \frac{1}{r}\right)^2.$$

Hiermee kan je opnieuw de waarde van $r$ vinden.

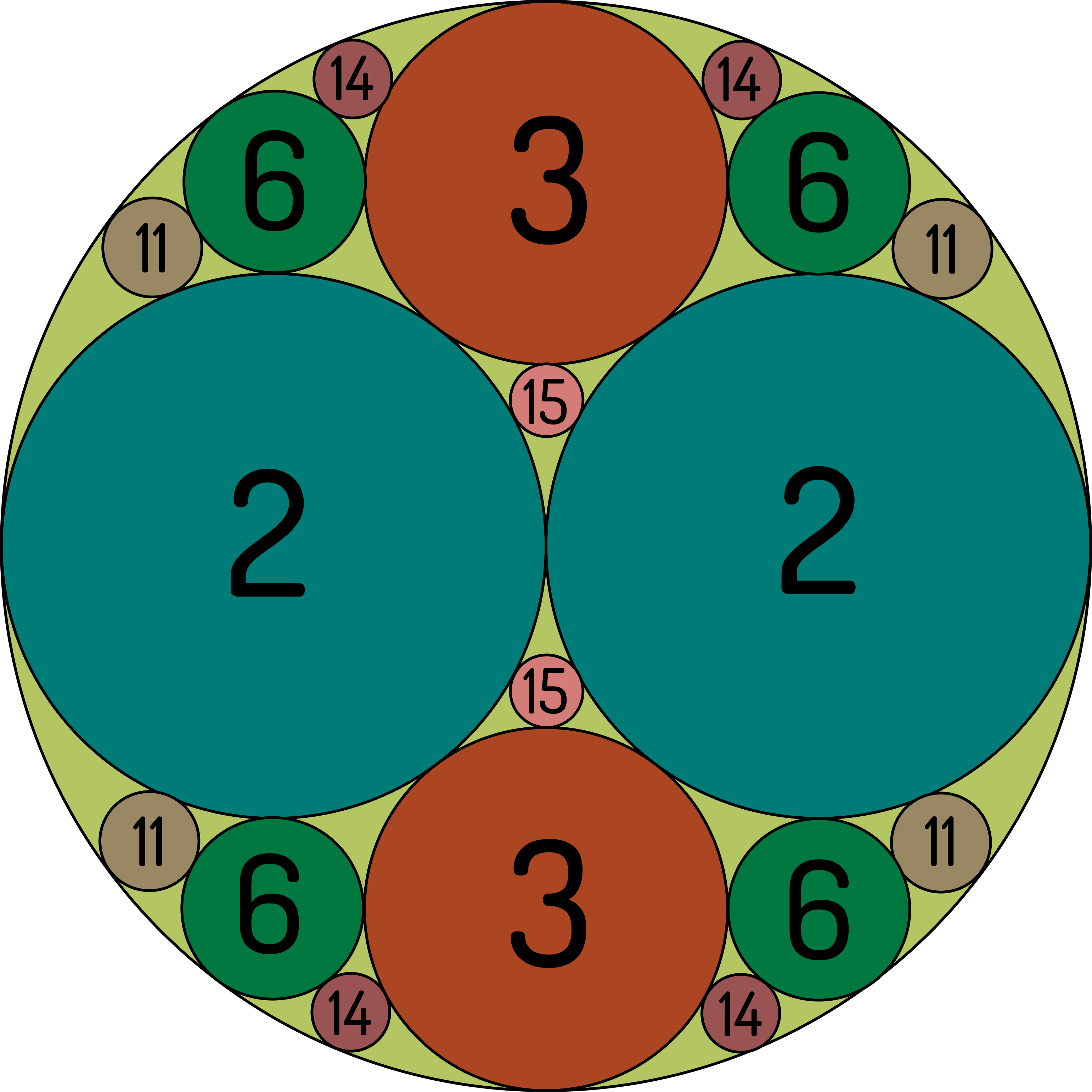
Als we nu nog extra cirkels toevoegen die raken aan wat er al is getekend, dan kunnen we met de formule van Descartes de stralen van die cirkels bepalen. Omdat deze formule zo eenvoudig is, zijn de waarden van die stralen vaak ook eenvoudige uitdrukkingen. In riguur 9 zijn er enkele getekend. We zijn vertrokken van een arbelos met $r_1 = r_2 = 1$ . De straal van elk van de cirkels is het omgekeerde van het getal in de cirkel. Voor de symmetrie van de figuur hebben we gewerkt met volledige cirkels.

 

Bronnen

Op het internet vind je een heleboel informatie over de arbelos. Het Zebraboekje nr. 30, van Floor van Lamoen: Passen en Meten met Cirkels - de arbelos van Archimedes, is ook zeker een aanrader.

Bekijk oplossing