Archimedes

Hoewel vrijwel niets uit het leven van Archimedes echt vaststaat, hieronder een aantal zaken die waarschijnlijk zijn.

Archimedes is in 287 voor Christus geboren in Syracuse op Sicilië.

Hij is één van de allergrootste wiskundigen ooit. Hij was in Alexandrië in de leer bij leerlingen van Euclides. Hij vond allerlei slimme apparaten uit zoals een schroef om water mee op te hevelen. Wiskundig was hij zijn tijd ver vooruit. Hij kon al de oppervlakte onder een parabool en de verhouding tussen de inhoud van een cilinder en een bol berekenen. 

In deze jaargang van Pythagoras zullen we een aantal van zijn uitvindingen zoveel als mogelijk is beschrijven met behulp van de technieken van toen.

Pi

Archimedes gebruikte nog geen symbool voor de verhouding tussen de omtrek en de diameter van een cirkel, hij beschreef deze gewoon in woorden. De oude Grieken gebruikten symbolen sowieso nog niet op deze manier, het symbool $\pi$ voor deze verhouding stamt pas uit het begin van de achttiende eeuw en werd uiteindelijk populair doordat de beroemde wiskunde Euler het gebruikte. Verderop zullen we op Archimedes’ benadering komen, maar hij beschrijft eerst de oppervlakte van een cirkel, dus daar gaan we eerst op in.

De oppervlakte van een cirkel

In de welbekende oppervlakteformule $O = \pi r^2$ komt het getal $\pi$ al voor. Bij Archimedes is dat nog niet zo, hij drukt de oppervlakte van een cirkel uit in termen van de straal en de omtrek van een cirkel. Zijn werk “Over het meten van een cirkel” begint met de volgende stelling: “De oppervlakte van een cirkel is gelijk aan die van een rechthoekige driehoek waarvan de ene rechthoekszijde gelijk is aan de straal en de andere rechthoekszijde gelijk is aan de omtrek van de cirkel.”

Opgave 1: Laat zien dat wat Archimedes schrijft, klopt met de formules die je geleerd hebt voor de omtrek en de oppervlakte van een cirkel.

We gaan Archimedes’ bewijs van deze bewering gedetailleerd bekijken. Zijn bewijs is een bewijs uit het ongerijmde. Dit betekent dat hij het tegendeel aanneemt van wat hij wil aantonen en dan laat zien dat dit tot een tegenspraak leidt. De conclusie moet dan wel zijn dat de aanname fout was.

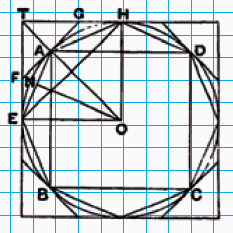
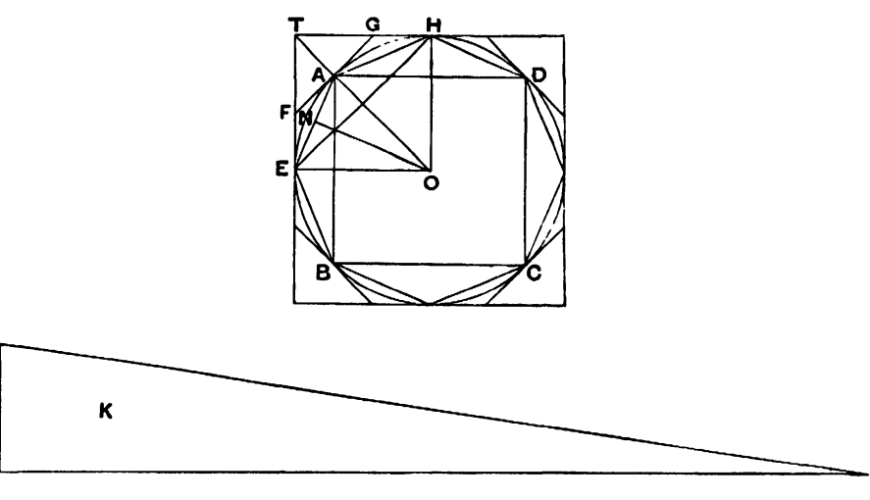
Hij begint met de aanname dat de oppervlakte van de cirkel niet gelijk is aan die van die beschreven driehoek. Dit kan twee dingen betekenen: de cirkel is ofwel groter dan de driehoek, ofwel kleiner. Archimedes splitst zijn bewijs dan ook in twee gevallen. Zoals je in figuur 2 kunt zien, noemt hij de oppervlakte van de driehoek $K$. De cirkel in figuur 1 is de cirkel waar het hier om draait. In zijn bewijs zullen we zien waarom hij al die lijntjes en vierkanten getekend heeft.

 

Geval I: stel dat de cirkel groter is dan $K$. Archimedes tekent een ingeschreven vierkant in de cirkel, vierkant $ABCD$ in het plaatje. Dat vierkant heeft uiteraard een kleinere oppervlakte dan de cirkel. Vervolgens deelt hij de lijnstukken $AB, BC, CD$ en $DA$ doormidden en de lijntjes vanuit middelpunt $O$ door die middens trekt hij door tot op de cirkel. Zo vindt hij punten $E$ en $H$ (en de twee andere soortgelijke punten die geen naam hebben gekregen). Nu heeft hij dus in feite een ingeschreven achthoek getekend. De oppervlakte van die achthoek is groter dan die van het vierkant, maar nog steeds kleiner dan die van de cirkel (hij ligt erbinnen, tenslotte). Archimedes zegt nu: dit kun je blijven doen, dus je kunt een ingeschreven zestienhoek, 32-hoek, enzovoorts maken. De oppervlakte van die ingeschreven veelhoeken wordt steeds groter, maar zal altijd kleiner blijven dan die van de cirkel. Alleen: op een gegeven moment moet er wel een veelhoek komen die een oppervlakte heeft die groter is dan K, de oppervlakte van de driehoek! Want we komen steeds dichter bij de oppervlakte van de cirkel door die veelhoeken te tekenen, en de aanname is dat de oppervlakte van de cirkel groter is dan K.

Stel nu dat die veelhoek bereikt is op een bepaald moment. Deze veelhoek heeft dus oppervlakte groter dan K en kleiner dan die van de cirkel. Er geldt:

$K$ < oppervlakte veelhoek < oppervlakte cirkel.

Bekijk nu een zijde van die veelhoek. Archimedes gebruikt in zijn uitleg zijde $AE$ in het plaatje, maar dat zou natuurlijk een zijde van een veelhoek met meer zijden kunnen zijn. Dan tekent hij het loodlijntje $ON$ op zijde $AE$ vanuit het middelpunt $O$. Omdat $ON$ binnen de cirkel ligt, is $ON$ kleiner dan de straal.

Opgave 2: Toon aan dat de oppervlakte van de veelhoek nu wel kleiner moet zijn dan K.

Kortom: er moet zo’n veelhoek bestaan met een oppervlakte groter dan K, maar daaruit volgt dan dat de oppervlakte ook kleiner dan $K$ moet zijn... Dat kan natuurlijk niet. De conclusie is dan dat de situatie in geval I niet kan voorkomen. De cirkel is dus sowieso niet groter dan $K$.

Geval II: stel dat de cirkel kleiner is dan $K$. Dit argument verloopt bijna hetzelfde, alleen werkt Archimedes nu met een omgeschreven vierkant, het buitenste vierkant in zijn plaatje. Hij bekijkt nu de raakpunten, bijvoorbeeld $E$ en $H$. Lijnstuk $EH$ wordt in twee gelijke stukken gedeeld door een lijn te trekken vanuit $O$, zo vindt hij punt $A$. In $A$ tekent hij een lijntje loodrecht op $OA$ en zo vindt hij de punten $F$ en $G$. Lijnstuk $FG$ is nu een zijde van een omgeschreven achthoek. Die achthoek heeft een oppervlakte die kleiner is dan die van het vierkant, maar nog steeds groter dan die van de cirkel.

Op dezelfde manier kun je verder gaan, zodat je een zestienhoek, 32-hoek, enzovoorts maakt, waarvoor steeds geldt: de oppervlakte van een veelhoek is steeds kleiner dan die van zijn voorganger, maar altijd nog groter dan die van de cirkel. Je gaat net zo lang door tot de oppervlakte van de veelhoek kleiner is dan $K$. Maar de oppervlakte van de veelhoek is uiteraard nog steeds groter dan die van de cirkel.

Opgave 3: Probeer aan te tonen dat de oppervlakte van de veelhoek nu wel groter moet zijn dan K.

Dus nu zien we dat de veelhoek, die we gemaakt hadden door steeds dichter naar de cirkel toe te kruipen tot de oppervlakte tussen $K$ en die van de cirkel in zat, opeens een oppervlakte blijkt te hebben die groter is dan $K$! Dat is weer een tegenspraak. Dus ook geval II kan niet voorkomen. 

Kortom: we hebben gezien dat de cirkel niet groter dan $K$ is en ook niet kleiner dan $K$ is. De enige mogelijkheid die overblijft, is dat de oppervlakte van de cirkel precies gelijk aan $K$ is. En dat is wat Archimedes wilde aantonen.

De omtrek van een cirkel en $\pi$

In stelling 3 gaat Archimedes dan vervolgens bepalen hoe groot de omtrek van een cirkel is in verhouding tot zijn diameter. Zijn stelling luidt: “de verhouding van de omtrek van elke cirkel tot zijn diameter is kleiner dan $3\frac{1}{7}$ en groter dan $3\frac{10}{71}$ “.

Opgave 4: Benader deze breuken op je rekenmachine en kijk hoe groot het verschil met $\pi$ is.

Je ziet aan deze formulering al dat hij, anders dan wij doen, niet één benadering geeft die zo dichtbij mogelijk zit. Hij klemt het getal dat hij zoekt in tussen twee waarden, en de reden daarvoor is de methode die hij gebruikte.

De methode lijkt een klein beetje op zijn argument van zojuist: hij gebruikt weer veelhoeken met steeds meer zijden, zodat de veelhoek steeds beter een stukje van de omtrek benadert. Van handige veelhoeken kan hij namelijk de verhoudingen van lengtes van de zijden wel berekenen met de meetkunde die hij tot zijn beschikking heeft.

Hij werkt overigens niet met echte lengtes, maar blijft werken met verhoudingen tussen lijnstukken. Dat sluit aan bij wat hij wil bewijzen hier, maar het sluit ook aan bij de meetkunde van Euclides die hij hier toepast. Euclides kende ook nooit exacte lengtes toe aan lijnstukjes, hij schreef ook altijd alleen over verhoudingen tussen lijnstukken of tussen oppervlaktes.

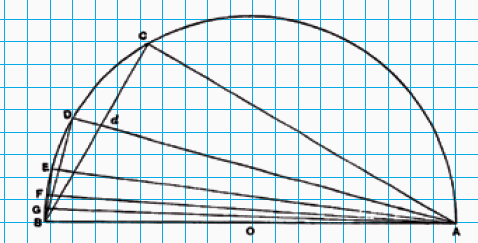
We kijken naar de bovengrens van $3\frac{1}{7}$. Archimedes gebruikt figuur 3. $O$ is weer het middelpunt, $AC$ staat loodrecht op straal $OA$ en hoek $AOC$ is een derde van een rechte hoek, dus 30˚.

Opgave 5: In driehoek AOC gelden de volgende verhoudingen: $OA : AC = \sqrt{3} : 1$ en $OC : CA = 2 : 1$ .

Waarom is dat zo?

Hint: driehoek $AOC$ is de helft van een gelijkzijdige driehoek.

Archimedes schrijft echter niet die $\sqrt{3}$ op, maar benadert, hij schrijft: $OA : AC > 265 : 153$. Als je die deling uitvoert zie je dat dit heel dicht bij $\sqrt{3} : 1$ zit en inderdaad een onderschatting is (maar het is behoorlijk nauwkeurig; de eerste vier decimalen zijn correct als je het omschrijft).

Archimedes gaat ook hier vervolgens de hoek in twee gelijke stukken delen door middel van lijn $OD$, waarbij $D$ op $AC$ ligt (hoek $AOD$ is dus 15˚, maar het is hier vooral relevant dat het de helft van de vorige hoek is).

Nu gebruikt hij een stelling van Euclides (stelling 3 uit boek VI van De Elementen): als je een bissectrice tekent in een driehoek, is de verhouding tussen de delen die op de overstaande zijde ontstaan gelijk aan die tussen de twee andere zijden in de driehoek. Met andere woorden, omdat OD hier de bissectrice is, volgt uit die stelling dat $CD : DA = CO : OA$.

Daarna gaat Archimedes aan de slag met verhoudingen. Omdat $CO : OA = CD : DA$ geldt ook $(CO + OA) : OA = CA : DA$ en dus $(CO + OA) : CA = OA : DA$.

Opgave 6: Ga na dat dat inderdaad volgt uit $CO : OA = CD : DA$.

Archimedes gaat verder met de volgende bewezen gegevens:

$(CO + OA) : CA = OA : DA$

$OA : AC > 265 : 153$

$OC : CA = 2 : 1 = 306 : 153$

Hij maakt de laatste twee verhoudingen zogezegd “gelijknamig”, zodat ze opgeteld kunnen worden. Want de conclusie is: $OA : AD = (CO + OA) : CA > (265 + 306) : 153 = 571 : 153$.

Nu kijkt Archimedes naar $OD^2$ en concludeert: $OD^2 : AD^2 > 349450 : 23409$ en dus $OD : DA > 591\frac{1}{8}: 153$.

Opgave 7: Ga na dat die verhouding tussen $OD^2$ en $AD^2$ inderdaad volgt uit de eerdere conclusies en controleer de verhouding $OD : DA$ die Archimedes hier geeft.

Wat hebben we hier nu aan? Op dezelfde manier gaat Archimedes verder: hij halveert hoek $AOD$ tot hoek $AOE$, die weer tot hoek $AOF$, die weer tot hoek $AOG$. Dan berekent hij (met alle tussenstappen precies op dezelfde manier als hierboven) dat $OA : AG > 4673\frac{1}{2}: 153.

Archimedes legt punt $H$ aan de andere kant van $A$ even ver als punt $G$. Dan is $GH$ de zijde van een omgeschreven regelmatige 96-hoek.

Opgave 8:

1. Leg uit waarom $GH$ de zijde van een regelmatige 96-hoek is.
2. Bereken uit de gevonden verhouding dat $\pi < 3\frac{1}{7}$

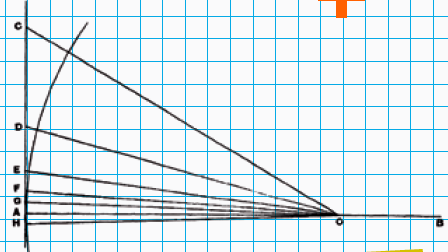
De ondergrens van $\pi > 3\frac{10}{71}$ gaat op een soortgelijke manier. Dan tekent hij niet een veelhoek in de cirkel, maar gebruikt hij echt de diameter helemaal, zoals in figuur 4 te zien is. Hij begint daar met driehoek $BAC$ waarbij hoek $A$ ook weer 30˚ is. Ook hier halveert hij hoek $A$ steeds en berekent hij de verhouding van achtereenvolgens $BC, BD, BE, BF$ en $BG$ met de diameter $AB$. Dit argument vereist net wat meer meetkundekennis (stelling van Thales, weer wat Euclides, stelling van de middelpuntshoek). Je kunt het vinden in het boek van Heath.

Bekijk oplossing