We gaan in dit artikel kijken hoe je efficiënt de lengte van de cyclus kunt bepalen.

Begrippen

We introduceren een paar begrippen: partities, staarten en cycli. Ten slotte bekijken we de begrippen graaien en zaaien.

Een partitie van een getal $N$ is een mogelijkheid om $N$ te schrijven als een som van een aantal positieve getallen. Bijvoorbeeld is $8 = 2 + 3 + 3$ een partitie. In principe is elke mogelijkheid om $N$ bonen in bakjes te plaatsen een partitie. Hieronder staat een overzicht van het aantal mogelijke partities voor kleine waarden van $N:$

N		$1$		$2$		$3$		$4$		$5$		$6$		$7$		$8$		$9$		$10$		$11$		$12$
partities		$1$		$2$		$3$		$5$		$7$		$11$		$15$		$22$		$30$		$42$		$56$		$77$

In het vorige nummer gaven we de opdracht om zelf de procedure graai te schrijven. Graai is een afbeelding die een partitie afbeeldt op een (andere) partitie. We kunnen Graai meerdere malen uitvoeren. Uiteindelijk kom je uit in cycli (het kan voorkomen dat een cyclus lengte $1$ heeft!). In figuur 1 is een voorbeeld van iteratief gebruik van de afbeelding Graai, voor $N = 8$.

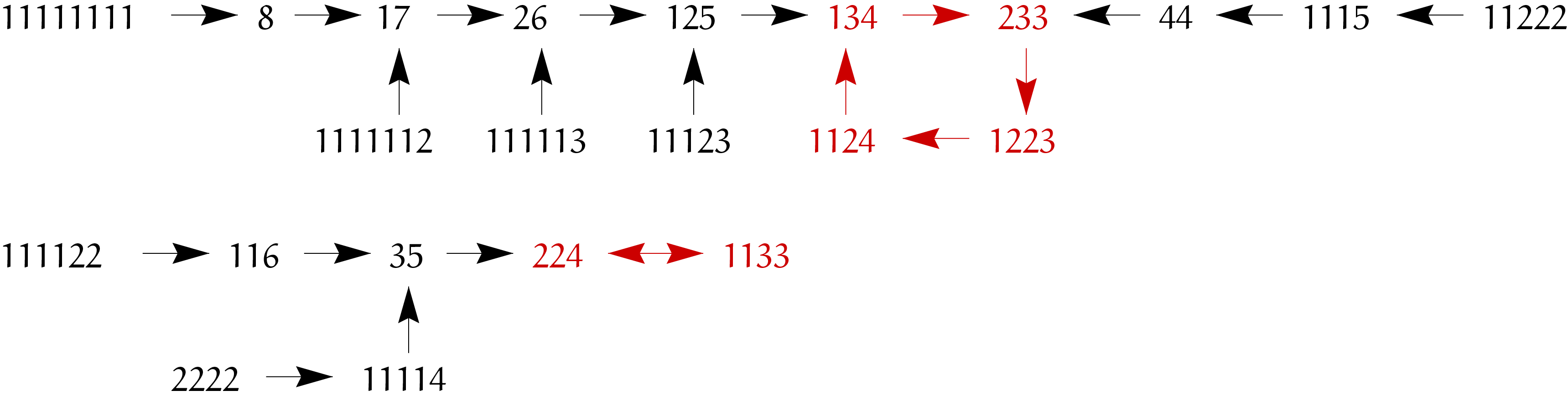
Figuur 1

Je ziet dat de afbeelding bestaat uit twee componenten. Als je in één van de componenten start, dan is het onmogelijk om in de andere component uit te komen. Een deel van de partities is rood gemarkeerd. Deze partities maken deel uit van de cycli. Eén van de cycli heeft lengte $4$ de andere lengte $2$. De zwarte partities noemen we staarten.

Ten slotte kun je je mogelijk ook iets voorstellen bij het begrip zaaien. In het originele bonenspel leeg je een bakje met bonen en verspreid je de bonen over de overige bakjes. In het geval van zaaien eisen we dat de bakjes die al één of meer bonen bevatten allemaal een boon extra krijgen. Uitgaande van $B$ bakjes, kun je alleen zaaien met bakjes die minimaal $B - 1$ bonen bevatten, immers het bakje zelf wordt leeggemaakt. Mochten er meer dan $B - 1$ bonen in een bakje zitten, dan wordt het restant van de bonen geplaatst in lege bakjes. De gerelateerde afbeelding Zaai doet precies het omgekeerde van de afbeelding Graai.

Merk wel op dat Graai altijd uniek bepaald is, terwijl Zaai niet hoeft te bestaan, of dat er twee (of meer) mogelijkheden voor Zaai zijn.

Eigenschappen van partities in de cycli

Wanneer is de cycluslengte $1$? We hebben $B$ bakjes met $K_1, K_2, \ldots , K_B$ bonen. We voeren de afbeelding Graai uit. Nu ziet de verdeling er als volgt uit: $K_1 - 1, K_2 - 1, \ldots, K_B-1, B$. Deze twee verdelingen moeten identiek zijn om inderdaad een cyclus van $1$ te krijgen. Om te beginnen: het aantal bakjes blijft $B$, dus $K_1 = 1.$ Voor $j > 1$ moet gelden dat $K_j - 1 = K_{j-1}$. Zo vinden we eenvoudig dat $K_j= j$, voor $1 \le j \le B$. Dus cycluslengte $1$ komt uitsluitend voor bij de getallen $1 = 1$, $3 = 1 + 2$, $6 = 1 + 2 + 3$, $10 = 1 + 2 + 3 + 4$, $15 = 1 + 2 + 3 + 4 + 5$, etc., de driehoeksgetallen.

Wat kun je zeggen over de permutaties die deel uit maken van de cycli? Hierboven hebben we de situatie al bekeken dat $N$ een driehoeksgetal is. Nu kijken we naar het geval dat $N$ geen driehoeksgetal is. Laat $D$ het verschil zijn tussen $N$ en het daaropvolgende driehoeksgetal. Laat verder $N + D = 1 + 2 + 3 + \cdots + B$. Merk op dat $0 < D < B$. Immers als $D = B$, dan is $N$ het voorafgaande driehoeksgetal. Laat nu $D_1, D_2, D_3, \ldots , D_B$ allemaal $0$ of $1$ zijn, zo dat $D_1+ D_2 + D_3 + \cdots + D_B = D$. Bijvoorbeeld in figuur 1 is $N = 8, $ het volgende driehoeksgetal is $10$ en dus is $D = 2$. Een partitie kan er als volgt uitzien: $1 - D_1, 2 - D_2, 3 - D_3, \ldots , B-D_B$. We gaan nu graaien. Als $D_1 = 1$, dan is het eerste bakje leeg, en valt er geen boon uit te halen, anders wel en is na Graai het betreffende bakje leeg. In het eerste geval worden er $ B - 1$ bonen verzameld. In het tweede geval is dat $B$ bonen. In het algemeen dus $B - D_1$. Het resultaat van Graai is $1 - D_2, 2 - D_3, 3 - D_4, \ldots, B-1-D_B, B-D_1$. Je ziet wat er gebeurt: De nullen en enen $D_1, D_2, D_3, \ldots , D_B$ worden cyclisch verwisseld. Als je Graai $B$ maal herhaalt dan staan $D_1, D_2, D_3, \ldots, D_B$ weer op hun originele plaatsen. Het gaat te ver voor dit artikel om te bewijzen dat met behulp van bovenstaande constructie alle partities in de cycli worden gevonden. Maar misschien vind je zelf een elegant en simpel bewijs. Dan zou het fijn zijn als je het ons toestuurt.

		Opdrachten
		1.		Schrijf een procedure voor zaai. Als zaaien mogelijk is, dan moet Zaai precies het juiste aantal permutaties weergeven. Probeer Zaai uit op $[2, 3, 4]$ en $[1, 1, 1, 2, 2, 4]$.
		2.		De cycluslengte hoeft niet gelijk te zijn aan $B$. Dat is bijvoorbeeld te zien bij $N = 8$, in figuur 1. Welke waarden kan de cycluslengte aannemen? Voor welke waarden van $N$ is de cycluslengte wel altijd gelijk aan $B$?
		3.		Verifiëer dat je, ongeacht de partitie waarmee je start, altijd uitkomt op $1, 2, 3, 4, \ldots , B$, als $N $ een driehoeksgetal is.
		4.		Schrijf een programma waarmee je alle partities in de cycli kunt berekenen inclusief de cycluslengte.
		5.		Schrijf een programma waarmee je het aantal componenten kunt bepalen. Hint: elke component bevat een eigen cyclus.
		6.		Kun je iets zeggen over het totale aantal partities in de cycli en het aantal componenten? Je hoeft geen formules af te leiden, maar mogelijk kun je iets zeggen voor kleine gevallen (tot $10$).