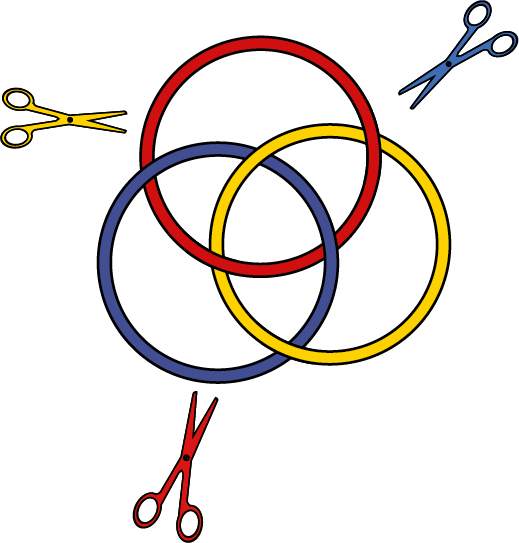
Borromeaanse ringen zijn drie met elkaar verstrengelde ringen en wel zo dat als je om het even welk van de drie ringen door zou knippen en wegneemt de twee overgebleven ringen volledig vrij komen te liggen. Als je bij voorbeeld in figuur 1 de gele ring doorknipt en weghaalt, liggen de rode en blauwe ring volledig los van elkaar. De blauwe ring ligt dan los op de rode. Knip je de blauwe ring door, dan liggen de gele en de rode ring vrij. En bij doorknippen van de rode ring liggen de blauwe en de gele los van elkaar.

Het motief kwam in de 15e eeuw voor in de drie ringen uit het familiewapen van de Noord-Italiaanse familie Borromeo (figuur 2).

Vandaar de naam voor deze  verstrengeling. Volgens historici stonden de ringen symbool voor de drie families Visconti, Sforza en Borromeo die door huwelijken nauw met elkaar verbonden waren. Naar alle waarschijnlijkheid gaat de oorsprong van het motief echter veel verder terug. 

Niet met platte ringen 

Wat op een tekening eenvoudig lijkt, is in de werkelijkheid niet altijd te realiseren. In 1987 bewezen Michael Friedman en Richard Skora dat met drie gewone platte stijve cirkelvormige ringen geen Borromeaanse combinatie is te maken. Probeer het zelf maar eens met een set ringen van sleutelhangers. Of maak ringen van stukjes ijzerdraad, dan zal je zien dat je ze moet vervormen. Je moet dus altijd platte cirkelvormige ringen vervormen en aanpassen om tot een Borromeaanse constellatie te komen. Zoals bijvoorbeeld in het logo van de IMU, International Mathematical Union (figuur 3). Uit dat logo is gemakkelijk af te leiden dat met drie platte ellipsen wel een ruimtelijke Borromeaanse verstrengeling is te maken.

Van netwerk naar lagen 

Vanuit het basismotief van de drie gekoppelde ringen zijn verschillende Borromeaanse structuren te ontwikkelen. Neem bij voorbeeld de langwerpige ringen uit figuur 4. Die kunnen worden uitgebreid door aan elk uiteinde op precies dezelfde manier twee andere langwerpige ringen op Borromeaanse wijze te koppelen (figuur 5). En op de uiteinden daarvan ook weer. Je krijgt dan wat je een Borromeaans netwerk zou kunnen noemen.

Vanuit zo'n netwerk is het een kleine stap naar de zogeheten Borromeaanse lagen. Die krijg je door in figuur 5 alle langwerpige ringen van dezelfde kleur met elkaar te verbinden. Je krijgt dan een golvend patroon van drie met elkaar verweven lagen zoals in figuur 6. Elke laag met een eigen kleur. Door om het even welke laag overal door te knippen en te verwijderen, blijven de overgebleven lagen als twee los van elkaar en op elkaar liggende tapijtjes over die nergens met elkaar zijn verbonden. Dus inderdaad Borromeaanse lagen. Dit soort verwevingen komen in verschillende culturen voor. Zo is figuur 7 afkomstig uit een Japanse vlakversiering. 

Van lagen naar 3D

Ga er nu even van uit dat de Borromeaanse lagen van figuur 6 zich inderdaad kunnen gedragen als soepele tapijtjes. Dan zijn die door buigen om te zetten in een cilindervormige structuur (figuur 8). En wanneer de opstaande randen van figuur 8 ook weer als Borromeaanse ringen worden verbonden, is een Borromeaanse kolom verkregen. Het is echter niet een enkele kolom, maar het zijn de drie met elkaar verstrengelde kolommen. Wanneer om het even van welke kolom de  verbindingen worden doorgeknipt zodat de betreffende kolom er aan stukjes tussen uit kan worden gehaald, dan zijn de overblijvende twee kolommen niet met elkaar verweven. De ene kolom zit als het ware om de andere heen. Net als bij de
ringen hebben alle drie kolommen afzonderlijk precies dezelfde vorm. 

De beeldengroep

De beeldengroep in crematorium Usselo is op te vatten als een drieluik. Dat drieluik wordt gevormd door de drie verstrengelde kolommen binnen, en twee elkaar omhullende kolommen en een afzonderlijke 'losgemaakte' kolom buiten (figuur 9a, b en c). Ondanks plaatsing van een deel binnen en twee delen buiten kan er niet aan worden getwijfeld dat die delen bij elkaar horen zoals de foto aan het begin van dit artikel toont. Binnen is het nog met elkaar verstrengeld zijn, maar buiten is het los laten – laten gaan. De drie verstrengelde kolommen in figuur 9a, de twee elkaar omhullende kolommen in figuur 9b en de afzonderlijke kolom uit figuur 9c hebben alle zes precies dezelfde vorm. Ze zijn in metaal uitgevoerd door Strobos Metaal uit Hengelo. 

Opbouw

Eerst zijn alle losse delen met behulp van een laser uitgesneden (figuur 10). Een aantal daarvan wordt vervolgens samengesteld tot 'niet platte ringen' (figuur 11) waarmee de kolommen worden opgebouwd. Zoals in figuur 9c is te zien bestaat elke kolom uit zes van die 'ringen', twee aan voor- en achterzijde en een aan de beide zijkanten. Voor elk van de drie delen van het drieluik wordt begonnen met een zo'n kolom. Daarna worden twee van die enkele kolommen omhuld met een tweede kolom. In figuur 9b is dat de groengekleurde kolom. Dat kan nog door de vooraf gemaakte ringen uit figuur 11 op een handige manier om de eerste kolom heen samen te stellen. Dan komt het moeilijkste werk want bij een van die twee elkaar  omhullende kolommen moet met de losse onderdelen uit figuur 10 de derde kolom worden opgebouwd. Dat moet zo gebeuren dat steeds drie ringen van drie verschillende kolommen op dezelfde manier worden verstrengeld zodat ze Borromeaanse ringen vormen. Het resultaat daarvan staat binnen in het crematorium (figuur 12). Na las- en slijpwerk zijn de  kolommen gestraald en met een kleur afgewerkt.

Borromeaanse knoop?

Jaren geleden maakte de inmiddels overleden Jan Marcus met een 'open' en drie 'gesloten' driehoekige strips een vervlechting van vier regelmatige driehoeken (figuur 13 en 14). Van de open driehoek moesten na vervlechting de eindjes netjes naar elkaar toe worden gebogen. Hij noemde deze vervlechting een Borromeaanse knoop. Was dat wel helemaal terecht? Stel je weet niet dat een van de driehoeken open is en je breekt met geweld een om het even welke driehoek uit deze  vervlechting. Liggen dan de overgebleven driehoeken steeds volledig vrij van elkaar? Denk daartoe steeds een van de driehoeken weg en kijk hoe het met de overgebleven drie zit. Met zijn omschrijving van Borromeaanse ringen als ringen die zo aan elkaar vastzitten dat ze geen van drieën van de andere kunnen worden gescheiden klopt de benaming van Jan Marcus. Inderdaad zo bekeken zijn de vier driehoeken zo met elkaar vervlochten dat ze geen van vieren zonder geweld van de andere gescheiden kunnen worden.