In 1799 verscheen in een blad van de Koninklijke Deense Academie van Wetenschap en Letteren een artikel van Caspar Wessel met de titel "Om Directionens analytiske Betegning, et Forsog, anvendt fornemmelig til plane og sphæriske Polygoners Oplosning" (Over de analytische beschrijving van de richting, een poging, voornamelijk toegepast op het oplossen van vlakke en sferische veelhoeken). Daarin beschreef hij hoe je met richtingen in het vlak en op een boloppervlak kunt rekenen. Dat was belangrijk voor hem want hij was op dat moment de Koninklijke Inspecteur van de Landmeters en daarmee verantwoordelijk voor de kwaliteit van de landkaarten. We bekijken hier vooral het rekenen met richtingen in het vlak.

Met 'richtingen' bedoelde Wessel wat wij nu vectoren noemen: een richting wordt bepaald door zijn hoek met een vaste gegeven halve rechte lijn (wij nemen daarvoor de positieve $x$-as) en zijn lengte.

De definities

Voor het optellen van richtingen gebruikte Wessel de kop-staart methode die we allemaal wel kennen. Als je twee vectoren hebt legt je het beginpunt van de tweede in het eindpunt van de eerste en de som is de richting van de vector van het beginpunt van de eerste naar het eindpunt van de tweede. Zoals Wessel toelichtte: "als we drie voet vooruit gaan en twee voet achteruit dan komt dat overeen met één voet voorwaarts" en "als een zijde van een driehoek van $a$ naar $b$ gaat en de tweede van $b$ naar $c$ dan is de derde zijde, die van $a$ naar $c$, de som".

Interessanter is zijn definitie van het product van twee vectoren. Eerst sprak hij een eenheid af, een lijnstuk waarmee de andere lijnstukken gemeten kunnen worden. De eenheid noteerde hij met $1$ (soms ook $+1$). Dan: het product van twee vectoren moet uit de eerste factor gevormd worden op precies dezelfde wijze als de tweede factor uit de eenheid gevormd wordt. Dat wil zeggen:

EERST de vectoren moeten zó zijn dat ze in het vlak waar de eenheid ligt geplaatst kunnen worden.

DAARNAAST wat betreft de lengte van het product: dat moet zich tot de lengte van de eerste factor verhouden als de lengte van de tweede factor tot de eenheid.

TEN SLOTTE als de eenheid, de eerste factor en de tweede factor een gemeenschappelijk beginpunt worden gegeven dan moet het product in het vlak van de eenheid
liggen en evenveel graden van de eerste factor afwijken, en aan dezelfde kant, als de tweede factor afwijkt van de eenheid, zodat de richtingshoek van het product (of zijn afwijking van de eenheid) gelijk is aan de som van de richtingshoeken van de factoren.

Dat is een hele mond vol maar ik heb het op deze manier opgeschreven om een klein beetje te laten proeven hoe Wessel zijn definities uitlegde. We kunnen het ook in een plaatje illustreren (zie figuur 1; in Wessels artikel staan geen plaatjes).

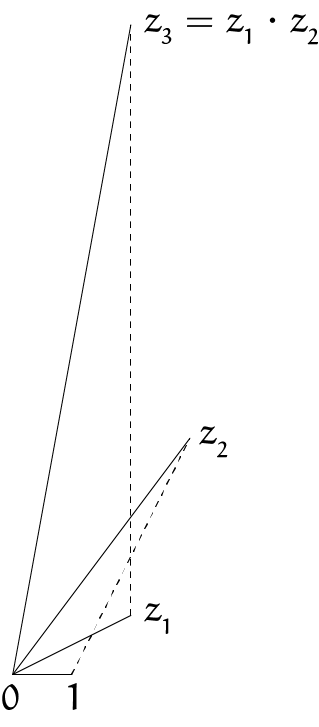
De driehoeken $[0, z_1, z_3]$ en $[0, 1, z_2]$ zijn gelijkvormig: de verhouding van de lengten van $[0, z_1]$ en $[0, z_3]$ is gelijk aan die van de lengten van $[0, 1]$ en $[0, z_2]$ (de tweede eis) en de hoek tussen $[0, 1]$ en $[0, z_2]$ is gelijk aan die tussen $[0, z_1]$ en $[0, z_3]$, zoals in de derde eis.

De wortel uit −1

Wessel noteerde de 'positieve rechtlijnige eenheid' met $+1$ en met $+\varepsilon$ "een zekere andere eenheid, loodrecht op de positieve eenheid, en met hetzelfde beginpunt". De richtingshoek van $+1$ is dan $0^{\rm o}$, die van $-1$ is $180^{\rm o}$, die van $+\varepsilon$ is $90^{\rm o}$ en die van $-\varepsilon$ is $-90^{\rm o}$ of $270^{\rm o}$. Volgens de regel dat de richtingshoek van een product de som van die van de factoren is krijgen we dan $(+1) \cdot (+1) = +1, \dots , (+\varepsilon) \cdot (+\varepsilon) = -1, \dots , (-\varepsilon) \cdot (-\varepsilon) = -1$ (er staan tien van zulke producten in het artikel). En Wessel concludeerde dat "$\varepsilon$ wordt $\sqrt{-1}$." Zie figuur 2.

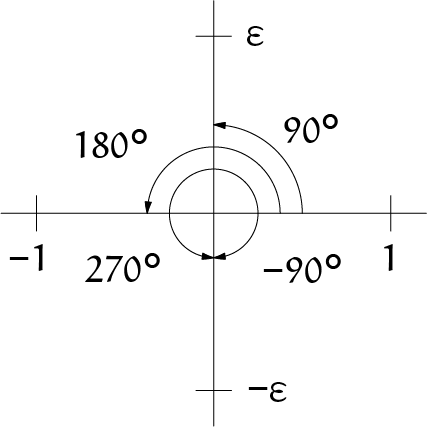
Op de $x$-as verandert er overigens niets, daar werkt deze vermenigvuldiging net zoals we voor reële getallen gewend zijn. Dankzij de meetkundige aanpak is bijvoorbeeld ook meteen duidelijk waarom twee negatieve getallen een positief product hebben: beide hebben een hoek van $180^{\rm o}$ en hun product dus een hoek van $360^{\rm o}$, wat overeenkomt met een hoek van $0^{\rm o}$. Wessel heeft dus in het platte vlak een optelling en vermenigvuldiging gemaakt die die van de reële getallen uitbreiden. En daarbij hebben we ook twee oplossingen, namelijk $\varepsilon$ en $-\varepsilon$, van de vergelijking $x^2 = -1$ gekregen.

Sinussen en Cosinussen

Wessel had wel door dat zijn vermenigvuldiging niet echt makkelijk uit te voeren was: stel dat je de $OA$ en $OB$ wilt vermenigvuldigen, met $A = (2, 1)$ en $B = (3, 4)$. De lengten van die lijnstukken zijn makkelijk te bepalen $(\sqrt{5}$ en $5)$ maar hun richtingshoeken niet.

Daarom keek hij naar de werking van die vermenigvuldiging op de eenheidscirkel. Hij begon met op te merken dat elke straal van de cirkel een richtingshoek, zeg $v$, heeft en dus te schrijven is als $\cos(v) + \varepsilon \sin(v)$ zoals in figuur 3.

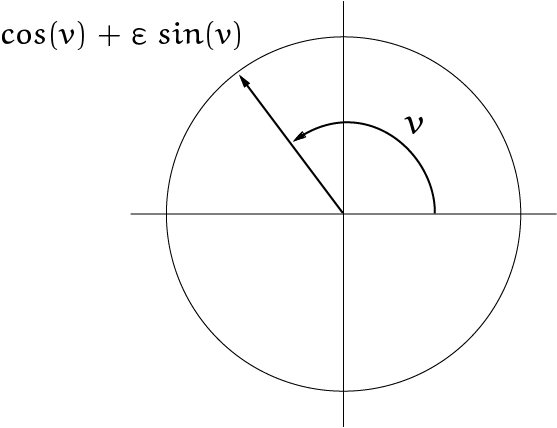
Voor alle duidelijkheid: men noemde elk lijnstuk van het middelpunt naar een punt op de cirkel een straal van de cirkel. Wat wij nu de straal noemen is dus de gemeenschappelijke lengte van alle stralen. Neem nog een straal, met richtingshoek $u$; dan is de richtingshoek van het product gelijk aan $v + u$, en dan kunnen we dat product schrijven als $\cos(v + u) + \varepsilon \sin(v + u)$.

Het product $(\cos(v) + \varepsilon \sin(v))(\cos(u) + \varepsilon \sin(u))$ kunnen we dus schrijven als $\cos(v + u) + \varepsilon \sin(v + u)$. Maar, schreef Wessel, we mogen ook gewoon de haakjes wegwerken tot

$$\cos(v) \cdot \cos(u) - \sin(v) \cdot \sin(u) + \varepsilon(\cos(v) \cdot \sin(u) + \cos(u) \cdot \sin(v))$$

waarbij we dus $\varepsilon^2 = -1$ gebruiken. Dat dit het juiste antwoord oplevert volgt uit de bekende gonioformules voor $\cos(v + u)$ en $\sin(v + u)$.

Makkelijker vermenigvuldigen

Wessel nam nu vier (gerichte) lijnen $a$, $b$, $c$, en $d$ van willekeurige lengte en wel zo dat $a + \varepsilon b$ en $c + \varepsilon d$ in hetzelfde vlak liggen als het lijnstuk $+1$. Dan mogen we het product $(a + \varepsilon b)(c + \varepsilon d)$ uitrekenen door de haakjes weg te werken: het is gelijk aan $ac - bd + \varepsilon (ad + bc)$.

BEWIJS. De lengte van $a + \varepsilon b$ noemen we $A$ en de richtingshoek $v$; en $c + \varepsilon d$ heeft lengte $C$ en richtingshoek $u$. Maar dan geldt $a + \varepsilon b = A\cos(v) + A\varepsilon\sin(v)$ en $c + \varepsilon d = C\cos(u) + C\varepsilon\sin(u)$ zodat $a = A\cos(v)$, $b = A\sin(v)$, $c = C\cos(u)$ en $d = C\sin(u)$. Per definitie geldt dan $(a + \varepsilon b)(c + \varepsilon d) = AC(cos(v + u) + \varepsilon sin(v + u))$ en dat is weer gelijk aan

$$AC(\cos(v) \cdot\cos(u) -\sin(v) \cdot\sin(u)) + AC\varepsilon(\cos(v) \cdot\sin(u) + \cos(u) \cdot\sin(v)).$$

Vervang nu $AC\cos(v) \cdot\cos(u)$ door $ac$, $AC\sin(v) \cdot\sin(u)$ door $bd$, enzovoort. Dan krijgen we wat te bewijzen was.

Nu is het product van de hierboven genoemde lijnstukken $OA$ en $OB$ snel uitgerekend. We hebben $OA = 2 + \varepsilon$ en $OB = 3 + \varepsilon 4$, dus

$$OA \cdot OB = (2 + \varepsilon)(3 + \varepsilon 4) = (6 - 4) + \varepsilon (8 + 3) = 2 + \varepsilon11.$$

Complexe getallen

Voor wie al wat van complexe getallen weet, zien de resultaten van Wessel er waarschijnlijk bekend uit; helemaal als je $\varepsilon$ door de imaginaire eenheid ${\rm i}$ vervangt.

Wat Wessel heeft gedaan is het omgekeerde van wat je in vrijwel alle boeken over complexe getallen ziet: daar begint men algebraïsch met de definitie $(a + b{\rm i})(c + d{\rm i}) = (ac - bd) + (ad + bc){\rm i}$ en leidt hier dan de meetkundige versies uit af.

Wessel begon met de meetkunde en eindigde met de algebra. Ik vind dat eigenlijk best mooi.