Inspiratie voor wiskunde is overal. In de middenberm van de A7, tussen Groningen en Winschoten, staat een enorm model van het aardgasmolecuul CH4. Zoals wellicht bekend bestaat aardgas chemisch gezien uit één koolstofatoom (C, van het Latijnse ' carbonium') en vier waterstofatomen (H, van 'hydrogenium', het meest voorkomende element in het heelal). Energetisch gezien zoeken de vier waterstofatomen zoveel mogelijk de ruimte. Ze staan daarbij op een vaste afstand van het koolstofatoom (de 'binding') en dus op maximale afstand van elkaar.

Ik vroeg mij af welke hoek twee van die waterstofatomen met het koolstofatoom maakten. (Waarom had ik mij dat trouwens nooit eerder afgevraagd?) Geen $90$ graden natuurlijk. Is het de bekende hoek van $120^{\rm o}$? Is het de net iets minder bekende hoek van $108^{\rm o}$ (van de regelmatige vijfhoek en het pentagram)? Of $135^{\rm o}$ dan misschien? Nee, geen van deze hoeken.

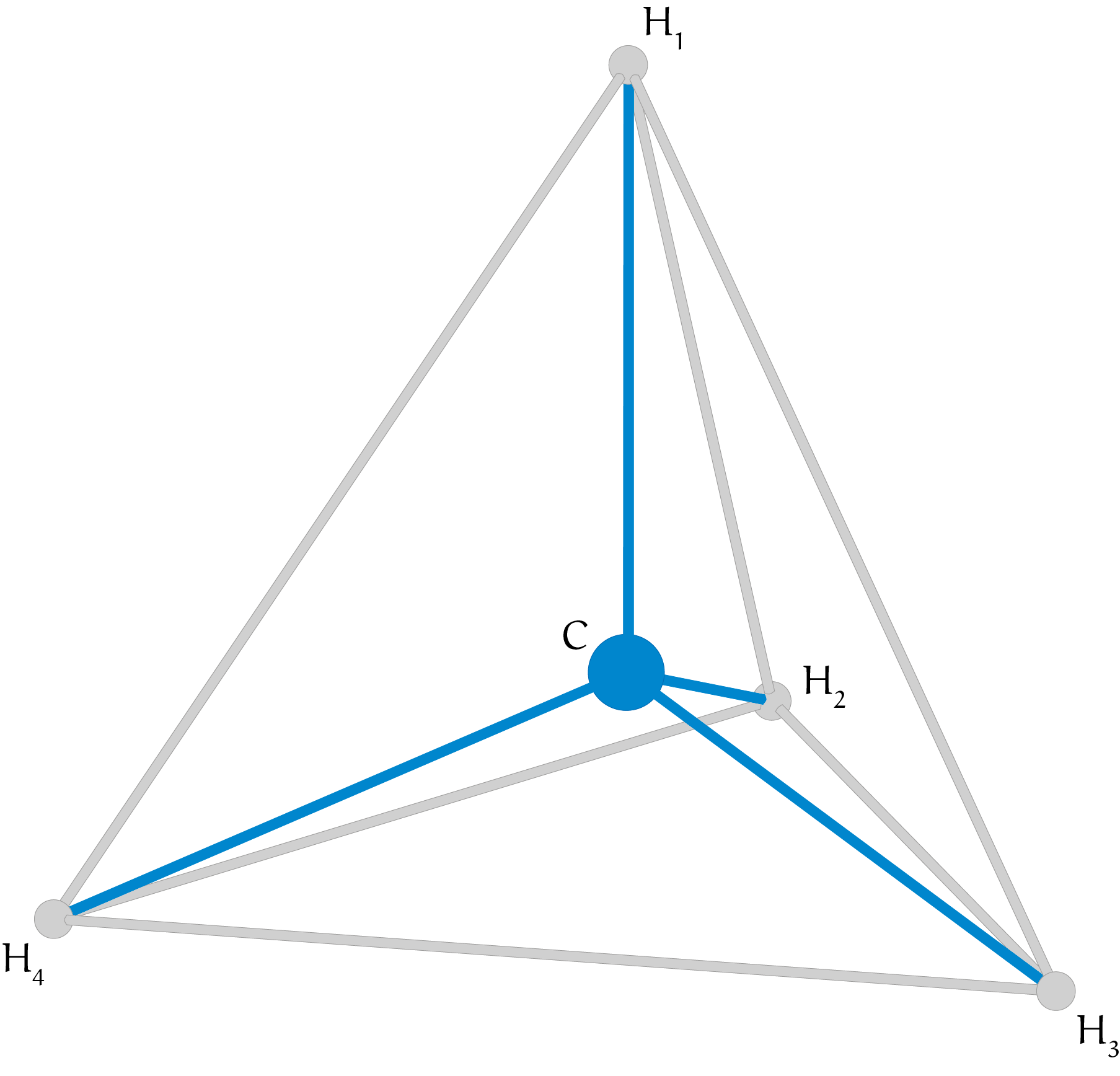
De oplossing zou kunnen beginnen met de constatering dat de vier punten $H_1$ tot en met $H_4$ in figuur 1 op een tetraëder liggen, met $C$ als middelpunt. In dat geval liggen de vier waterstofatomen namelijk zo ver mogelijk van elkaar. Stel de coördinaten van het koolstofatoom $C$ op $(0, 0, 0)$. De vier waterstofatomen $H_1$ tot en met $H_4$ liggen elk op een vaste afstand, zeg $1$, van $C$. Stel bijvoorbeeld $H_1 = (0, 0, 1)$. Alle drie de punten $H_2$, $H_3$ en $H_4$ liggen dan in een horizontaal vlak met $z$-coördinaat $-\tfrac{1}{3}$. Dat is in te zien doordat bij een tetraëder het middelpunt (hier $C$) als coördinaten het gemiddelde is van de vier hoekpunten. Dat geldt dus ook voor de hoogte (de $z$-coördinaat). Aangezien $H_1$ een $z$-coördinaat van $1$ heeft, moeten de andere drie punten ieder een $z$-coördinaat $-\tfrac{1}{3}$ hebben.

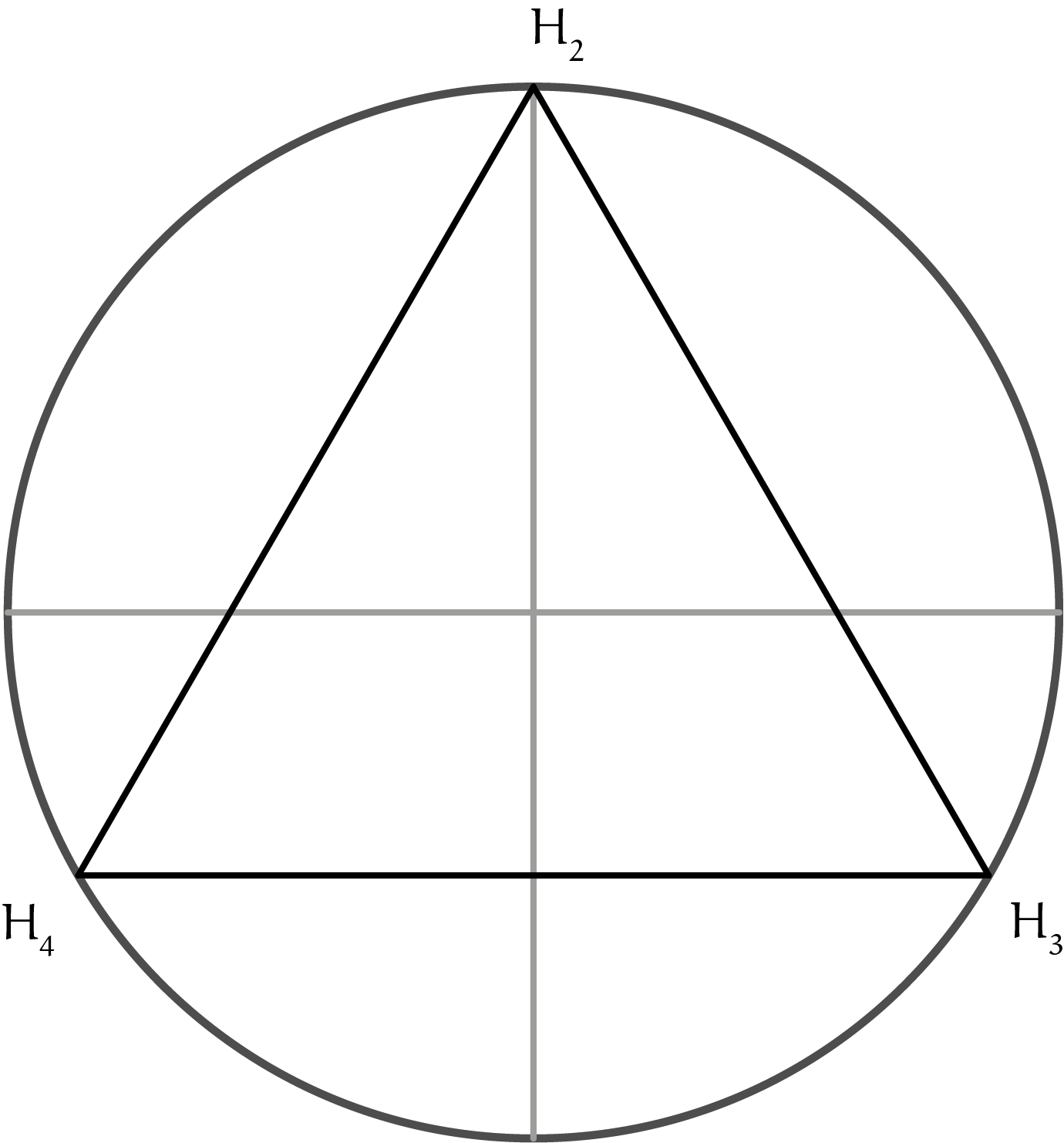
Stel dat $H_2$ de coördinaten $(0, y, -\tfrac{1}{3})$ heeft (met $y \ge 0$). De afstand van $H_2$ tot $C$ is $1$, dus geldt: $0^2 + y^2 + (-\tfrac{1}{3})^2 = 1$. Hieruit volgt $y = \tfrac{2}{3}\sqrt{2}$. Als we de het hoekpunt $H_i$ coördinaten $(x_i, y_i, z_i)$ geven hebben we voor $H_1 = (0, 0, 1)$ (dus $x_1 = 0$, $y_1 = 0$ en $z_1 = 1)$ en we hadden al gevonden $z_2 = z_3 = z_4 = -\tfrac{1}{3}$. Net als voor $z_i$ geldt ook dat het gemiddelde van $y_i = 0$. Met $y_1 = 0$, $y_2 = \tfrac{2}{3}\sqrt{2}$ en $y_3 = y_4$ krijgen we $y_3 = y_4 = -\tfrac{1}{3}\sqrt{2}$. Nu hebben we alleen nog $x_3$ en $x_4$ nodig. We weten al dat $x_4 = -x_3$ en volgens Pythagoras geldt $x_3^2+y_3^2+z_3^2=1$ waaruit volgt dat $x_3=\tfrac{1}{3}\sqrt{6}$. Nog even alles op een rijtje:

$C=(0,0,0)$
$H_1=(0,0,1)$
$H_2=(0,\tfrac{2}{3}\sqrt{2},-\tfrac{1}{3})$
$H_3=(\tfrac{1}{3}\sqrt{6},-\tfrac{1}{3}\sqrt{2},-\tfrac{1}{3})$
$H_4=(-\tfrac{1}{3}\sqrt{6},-\tfrac{1}{3}\sqrt{2},-\tfrac{1}{3})$

Het gevolg is dat $|H_3H_4|=\tfrac{2}{3}\sqrt{6}$. De gezochte hoek $\alpha=\angle H_3CH_4$ kunnen we nu vinden met de cosinusregel:

$|H_4H_3|^2=|CH_3|^2+|CH_4|^2-2|CH_3|\cdot|CH_4|\cdot\cos(\alpha)$ of $\frac{8}{3}=1+1-2\cos(\alpha)$.

Dus $\alpha=\cos^{-1}\left(-\tfrac{1}{3}\right)=\arccos\left(-\tfrac{1}{3}\right)\approx 109{,}4712^{\rm o}$.