We noemen een dynamisch systeem chaotisch wanneer een kleine verandering in de beginwaarden van het systeem ertoe kan leiden dat het systeem volledig ander gedrag vertoont. Chaos maakt het moeilijk en vaak zelfs onmogelijk om op lange termijn voorspellingen te doen. Dit is bijvoorbeeld de reden waarom weersvoorspellingen niet meer dan een paar dagen vooruit gegeven worden. Ook al is er geen willekeur in een dynamisch systeem, wat bijvoorbeeld wel bij de prijzen op de aandelenbeurs het geval is, dan nog kan het systeem chaotisch zijn. In dit artikel bespreken we een eenvoudig model voor populatiegroei van muizen dat chaotisch gedrag vertoont. We beginnen met een voorbeeld van een dynamisch systeem uit de populatiedynamica. Beschouw een muizenpopulatie in een pakhuis waar de muizen niet in of uit kunnen. Stel dat er op tijdstip $0$ een hoeveelheid $M_0$ muizen in het pakhuis aanwezig is, en dat de muizenpopulatie per maand groeit met groeifactor $p > 1.$ Hoeveel muizen zijn er dan na één maand? Na twee maanden? En na $n$ maanden?

Dynamisch systeem

Een dynamisch systeem beschrijft de evolutie van een systeem in de tijd. De evolutie wordt gevangen door een functie $f.$ Na één tijdstap bevindt $x$ zich op $f(x).$ Na twee tijdstappen op

$f^2(x) = f(f(x)).$ Na n tijdstappen bevindt $x$ zich op $$f^n(x)= \begin{matrix} \underbrace{f\left(f\left(\cdots f\left(f(x) \right ) \right ) \right )}\\ n\mbox{ keer} \end{matrix}.$$

We kunnen de evolutie van de muizenpopulatie beschrijven met de functie $f(x) = px.$ Na één maand zullen er $f(M_0) = pM_0$ muizen zijn, na twee maanden $f^2(M_0) = f(f(M_0)) = p(pM_0) = p^2M_0,$ en na $n$ maanden zijn het er $$f^n(M_0)= \begin{matrix} \underbrace{f\left(f\left(\cdots f\left(f(M_0) \right ) \right ) \right )}\\ n\mbox{ keer} \end{matrix} = p^nM_0.$$. Dit betekent dat de hoeveelheid muizen ongeremd zal blijven groeien, omdat we verondersteld hebben dat $p > 1.$

Opgave 1

Stel dat er $100$ muizen in het pakhuis zijn en dat er voor elke twee muizen elke maand een nieuwe muis bij komt. Beredeneer dat $p = 1{,}5.$ Hoeveel muizen zijn er na twee jaar?

Indiana Jones heeft last van de ongeremde groei van ratten.

Ongeremde groei is natuurlijk niet realistisch als we muizen in een pakhuis bekijken. Het antwoord dat je in opgave 1 hebt gevonden past niet eens in een pakhuis! Dit komt natuurlijk doordat we een erg simpel model hebben gekozen. Er zijn biologische redenen waarom de muizenpopulatie niet ongeremd kan groeien: als er te veel muizen zijn zal er onvoldoende voedsel in het pakhuis zijn om elke muis te laten overleven en zullen er dus muizen sterven. Voor grote aantallen muizen lijkt het dan alsof er netto minder muizen bij komen. Laat a de maximale hoeveelheid muizen in het pakhuis zijn waarvoor de muizenpopulatie ongeremd kan groeien. We passen het model voor de populatiegroei als volgt aan:

Bij “weinig” muizen $(x \le a)$ is er genoeg voedsel. We nemen aan dat de muizenpopulatie, die we nu met het symbool $T$ aangeven, in dit geval per maand groeit met groeifactor $p > 1,$ zoals eerst. Dus voor $0 \le x \le a$ beschrijven we de evolutie van het model met de functie $T(x) = px.$

Bij “te veel” muizen $(x > a)$ is er onvoldoende voedsel. Er zullen muizen sterven van de honger. Hoe meer muizen er zijn, hoe meer muizen er zullen sterven. Natuurlijk blijven de muizen zich wel voortplanten. Netto zal door de honger de muizenpopulatie minder hard groeien en bij heel veel muizen zal de populatie zelfs krimpen. Dit gedrag beschrijven we met de functie $T(x) = p(2a - x)$ voor $a < x \le 2a.$ We nemen verder aan dat de muizenpopulatie instort als $x > 2a.$ De muizen moeten zo erg om voedsel vechten dat geen enkele muis genoeg voedsel vindt om te overleven.

Samenvattend kunnen we het functievoorschrift voor de evolutie dit wat realistischere model opschrijven als

$$T(x)=\left\{\begin{array}{lll} px & \mbox{als} & 0 \le x \le a\\ p(2a-x) & \mbox{als} & a < x \le 2a\\ 0 & \mbox{als} & x > 2a \end{array}\right..$$

De functie heeft een knikpunt in $x=a.$ Links van het knikpunt is de functie lineair met richtingscoëfficiënt $p$ en rechts van het knikpunt is de functie lineair met richtingscoëfficiënt $-p.$

Om het rekenen te vergemakkelijken schalen we de vergelijkingen. Het getal $x$ stelt nu een fractie voor van een grote hoeveelheid muizen. We kiezen voor de parameters $p = 3$ en $a = \frac12.$ We krijgen de zogeheten tentafbeelding.

Tentafbeelding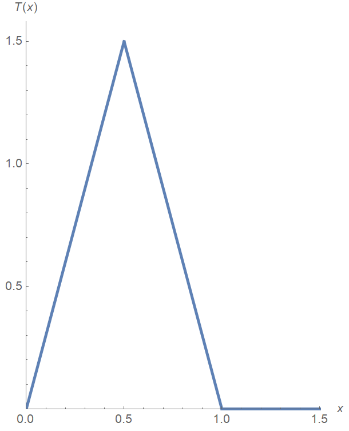

De tentafbeelding wordt gegeven door de functie

$$T(x)=\left\{\begin{array}{lll}3x & \mbox{als} & 0 \le x \le \frac{1}{2}\\3-3x & \mbox{als} & \frac{1}{2} < x \le 1\\0 & \mbox{als} & x > 1\end{array}\right. $$

We gaan de dynamica van de tentafbeelding nu onderzoeken. We zijn geïnteresseerd in het gedrag van punten binnen het dynamisch systeem. Wat is de uitkomst van $T^n(x)$ voor een bepaald punt $x$ bij een grote waarde van $n$? Hoe hangt dit gedrag af van de waarde van $x$?

Dekpunten en periodieke punten

Een dekpunt is een punt $x$ zodat $T(x) = x.$ Het aantal muizen blijft constant en het systeem is in evenwicht.

Een uiteindelijk dekpunt is een punt $y$ zodat $T^{m+1}(y)=T^m(y)$ voor een zekere $m > 1.$ Als $y$ een uiteindelijk dekpunt is, dan is $x = T^m(y)$ dus een dekpunt. Het aantal muizen evolueert naar een vast aantal, wat zelf in evenwicht is.

Een periodiek punt met periode $n+s$ is een punt $x$ zodat $T^n(x) = x$ maar $T^k(x) \neq x$ als $1 \le k < n.$ Het aantal muizen doorloopt een periodiek patroon.

We beginnen met een rekenvoorbeeld. Neem $x=\frac13.$ Omdat $\frac13 < \frac12$ is de uitkomst gelijk aan $T(\frac13)=3(\frac13)=1.$ We gaan verder: $T^2(\frac13)=T(T)\frac13))=T(1)=3-3\cdot 1=0,$ want $1 > \frac12.$ Het volgt dat ook $T^3(\frac13)=T(T^2(\frac13))=T(0)=3\cdot 0=0,$ en omdat $x=0$ door de tentafbeelding op $0$ wordt afgebeeld, kunnen we concluderen dat $T^n(\frac13)=0$ voor alle $n\ge 2.$ Het punt $x=0$ is een dekpunt en $x=\frac13$ wordt een uiteindelijk dekpunt genoemd. In onze muizencontext betekent dit dat wanneer we beginnen met een (geschaalde) populatie van $\frac13$ muizen, de muizen na twee tijdstappen allemaal dood zijn. En als er geen muizen zijn, zullen er op elk volgend tijdstip ook geen muizen zijn.

Opgave 2

Een dekpunt is een punt $x$ zodat $T(x) = x.$ In een dekpunt is het systeem in evenwicht. Bij deze beginvoorwaarde $x$ blijven er altijd $x$ muizen: er komen net zoveel muizen bij als er doodgaan. Het is makkelijk na te gaan dat $T(0) = 0,$ dus $x_0=0$ is een dekpunt. Vind nog een dekpunt $x_1$ van de tentafbeelding.

Het systeem is erg gevoelig voor de beginvoorwaarden. Het punt $x_0=0$ is een dekpunt, maar het is makkelijk na te gaan dat we voor $0\lt x\ll 1$ hebben dat $T(x) > x.$ De populatie zal groeien voor kleine waardes. Dat is ook te verwachten: zonder een muis kunnen er geen nieuwe jonge muizen bij komen, maar als we met een paar muizen beginnen zal de populatie snel gaan groeien. Dit zal net zo lang doorgaan totdat de waarde $T^n(x) > x_1,$ waar $x_1$ het dekpunt is dat je bij opgave 2 hebt gevonden. De populatie zal vanaf dan gaan krimpen. Het is mogelijk dat dan $T^{n+1}(x)=x.$ Zo’n punt $x$ heet een periodiek punt. Er zijn in dit systeem oneindig veel punten, willekeurig dicht bij het dekpunt $0,$ die periodiek zijn. Dit ga je onderzoeken in opgave 5. Dit gedrag is een hint dat het systeem chaotisch is.

Om het chaotische gedrag van de tentafbeelding beter te begrijpen, ga je in de volgende opgave op zoek naar dekpunten en periodieke banen in de tentafbeelding.

Opgave 3

Bereken een paar uiteindelijke dekpunten van de tentafbeelding.

Er is een leuke manier om grafisch alle uiteindelijke dekpunten van de tentafbeelding te vinden. Hiervoor teken je de tentafbeelding met de lijn $y=x.$ De dekpunten van de afbeelding zijn de snijpunten van de grafiek met de lijn $y=x.$ Begin nu in een dekpunt en beweeg horizontaal naar een van de twee lijnstukken van de tent. De $x$-coördinaat van het gevonden punt is een uiteindelijk dekpunt! Beweeg vervolgens verticaal naar de lijn $y=x$ en daarna weer horizontaal naar een van de twee lijnstukken van de tent. Op deze manier kun je oneindig veel uiteindelijke dekpunten vinden. Dit zijn beginwaarden waarvoor de muizenpopulatie uiteindelijk in evenwicht komt. Onderstaande figuur illustreert hoe uiteindelijke dekpunten die uiteindelijk in het dekpunt $x= 0$ komen kunnen worden gevonden. Ga verder in de figuur en probeer in de andere figuur zelf eens grafisch een aantal uiteindelijke dekpunten te vinden die worden afgebeeld op het andere dekpunt van de tentafbeelding.

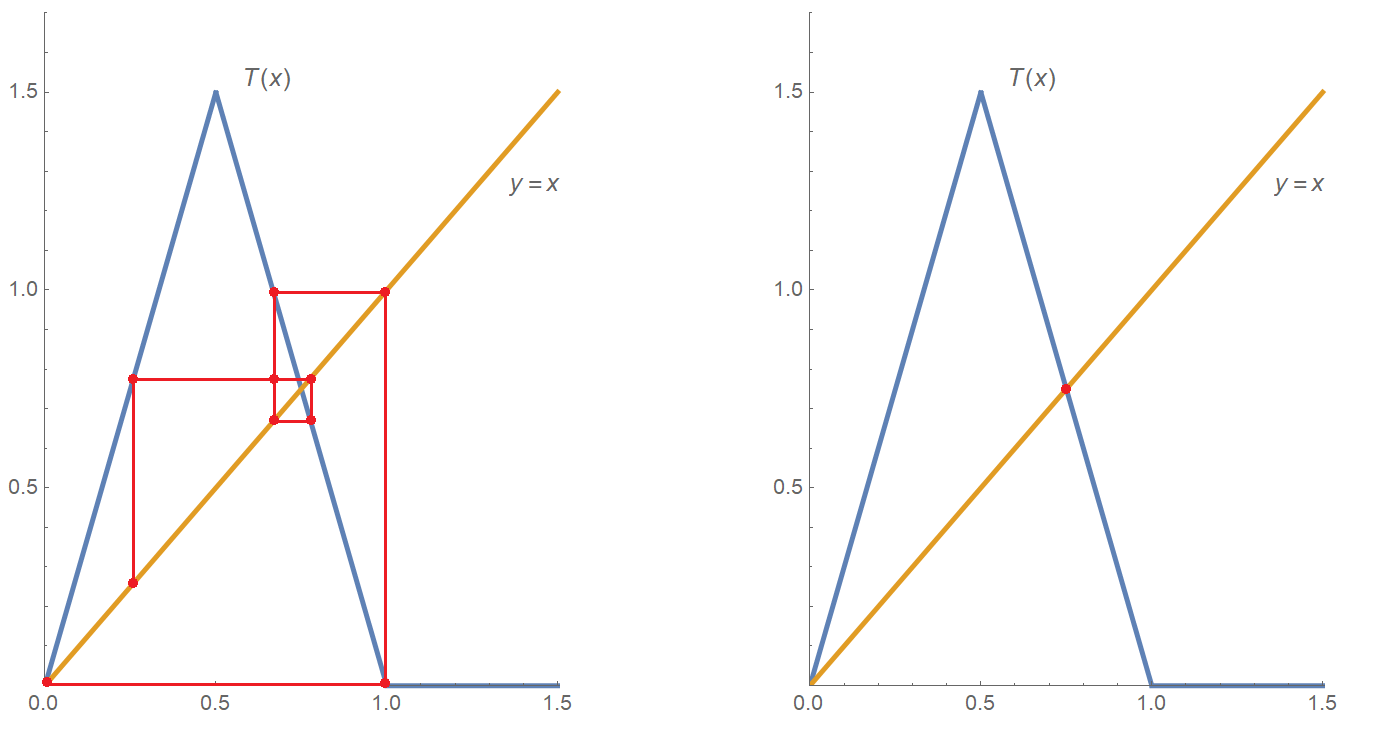De $x$-coordinaten van de rode stippen zijn alle (uiteindelijke) dekpunten die uiteindelijk in het dekpunt $x=0$ uitkomen. Probeer in de rechter grafiek zelf uiteindelijke dekpunten te vinden die in het dekpunt $x_1$ van opgave 2 terechtkomen.

Opgave 4

Bepaal het functievoorschrift van $T^2(x)$ en teken de grafiek. Laat zien dat als $x$ een periodiek punt van periode $2$ is, dat $x$ een dekpunt moet zijn van $T^2.$ Hoeveel periodieke punten met periode $2$ zijn er?

Opgave 5

(een breinbreker)

Bedenk hoe de grafiek van $T^n$ voor willekeurige $n$ eruit moet zien. Laat zien dat er oneindig veel periodieke punten zijn, met willekeurig grote periode.

We hebben gezien dat $T(x) = 0$ als $x=\frac13.$ Maar het is eenvoudig na te gaan dat $T(x)=0$ voor alle $\frac13 \le x \le frac23.$ De gehele muizenpopulatie sterft uit in één stap voor al deze $x.$ Als nu $\frac19 \le x \le \frac29$ of $\frac79 \le x \le \frac89$ dan is $\frac13\le T(x) \le \frac23,$ dus $T^2(x)=0.$ Voor al deze beginvoorwaarden gaat de muizenpopulatie dood in twee stappen. In figuur 1 is grafisch ook aangegeven voor welke punten de muizenpopulatie uitsterft in drie en vier stappen.

In de eerste lijn is in rood aangegeven waar de muizenpopulatie in één tijdstap uitsterft. In de tweede lijn is in rood te zien wanneer de muizenpopulatie in één of twee tijdstappen uitsterft, etc. De limiet van de blauwe punten zijn de beginvoorwaarden waarvoor de muizenpopulatie nooit uitsterft.

Dit patroon gaat in het oneindige door. In de limiet, dus voor $n \rightarrow \infty,$ zitten er nog steeds punten in de blauwe limietverzameling. Bijvoorbeeld het dekpunt $x_1$ wat je bij opgave 2 hebt gevonden, alsmede alle uiteindelijke dekpunten die in $x_1$ terecht komen, zitten in de blauwe limietverzameling. We zien dat het dynamisch systeem heel chaotisch is: de uiteindelijke ontwikkeling van het systeem hangt heel sterk af van de beginvoorwaarden. Als we een punt nemen uit de blauwe verzameling zal de muizenpopulatie niet uitsterven, maar punten willekeurig dichtbij zijn rood, en daarvoor sterft de populatie wel uit. 

De blauwe limietverzameling uit figuur 1 is een voorbeeld van een fractal: als je inzoomt op een klein stuk van de fractal ziet het eruit als het geheel. Fractals verschijnen vaak in chaotische dynamische systemen. In dit artikeltje hebben we gekeken naar eendimensionale dynamica. Alleen de muizenpopulatie werd gemodelleerd. Je kan je ook modellen voorstellen waarbij meerdere diersoorten tegelijk gemodelleerd worden, waar de dieren elkaar bijvoorbeeld op kunnen eten. Tijdens dit soort interacties kunnen veel gecompliceerdere fractals tevoorschijn komen.

Een fractal uit de complexe dynamica. Deze fractal is een tweedimensionaal analogon van de fractal in figuur 1.

Andere fractals zijn te zien in figuren 2 en 3. De fractals uit figuur 3 kun je ook met het blote oog in de natuur tegenkomen. Fractals hebben heel bijzondere wiskundige eigenschappen: zo hebben ze bijvoorbeeld een “gebroken dimensie”. De dimensie is niet meer een geheel getal, de fractal uit figuur 1 heeft bijvoorbeeld een gebroken dimensie van $\log_3(2) = 0{,}6309\dots.$ Kom naar de masterclass “Chaos en Dynamica” aan de Vrije Universiteit Amsterdam als je hier meer van wilt weten!

Masterclass Chaos en Dynamica

Zit je in 4, 5 of 6 VWO en zou je hier graag meer over leren? De opleiding Wiskunde van de Vrije Universiteit organiseert in samenwerking met Bètapartners de masterclass Chaos en Dynamica. In deze masterclass leer je meer over dynamische systemen en wat chaos betekent. We gaan verschillende dynamische systemen analyseren, en komen uiteindelijk via de Cantorverzameling uit bij fractals. Fractals spelen een belangrijke rol in de chaostheorie. Een fractal is een meetkundige figuur die opgebouwd is uit delen die gelijkvormig zijn met de figuur zelf. Als eindopdracht ontwerp je je eigen fractal en presenteer je deze op een wetenschappelijke postermarkt. We maken in deze masterclass geregeld gebruik van het computerprogramma Mathematica.

Data masterclass

Vrijdag 15 november 13.00-17.00

Vrijdag 22 november 13.00-17.00

Vrijdag 6 november 12.30-16.00 (postermarkt)

De masterclass wordt ook in april 2020 gegeven.

Inschrijven kan op

www.betapartners.nl/masterclass-chaos-en-dynamica/